Численное интегрирование.Пусть на отрезке (а;b) задана ф-я с помощью точек а=x0<x1<…<xn=в. Разобьем отрезок (а;в) на каждом из них выберем произвольную точку
Метод прямоугольника и трапеции. трапеции: используют лин интерполяцию, т.е. график ф-и y=f(x)представ в виде ломаной, соед. Точки(xi;yi) В этом случае площадь всей фигуры складывается из площадей трапеций:
Метод Симсона: Разобьем (а;в) на четное число n равных отрезков (x0;x2), (x2;x4),(xi-1;xi+1)…(xn-2;xn). На каждом отрезке подинтегр ф-ю f(x) замен интерполяц многочленом 2 степени. В качестве
Элементарную площадь Si м.б. вычислена с помощью опред интеграла. Суммируя получ выраж для Si Ф-ла Симсона: Метод Монте-Карло: x-одномерно распред случ величина на (а;в). Плотность ее распределения задаеться соотношением:
10. Рассмотрим дифур Метод последовательных приближений: Пустьдано диф уравнение
11. Методы Эйлера и Рунге-Кутта для решения дифференциальных уравнений.
Метод Эйлера: Пусть дано диФУР y'=f(x;y) и нач. усл. y(x0)=y0. Выбрав малый шаг h xi=x0+ih. y'=(y2-y1)/h (y1-y0)/h=f(x0;y0) y1=y0+hf(x0;y0) y2=y1+hf(x1;y1) … yn=yn-1+hf(xn-1;yn-1) Т.о. получим ломаную Эйлера, которая приближает искомое решение y(x). Первая модификация: xi+1/2=xi+h/2; yi+1/2=yi+h/2; fi+1/2=f(x i+1/2;y i+1/2) y i+1/2=yi+hf i+1/2. Вторая модификация: yi+1=yi+hf(xi;yi); yi+1=yi+h(f(xi;yi)+fi+1)/2. Метод Рунге-Кутта: Дано то же самое Выберем шаг h и введем обозначения: xi=x0+ih; yi=y(xi). Рассмотрим числа ai=hf(xi;yi); bi=hf(xi+h/2;yi+h/2); ci=hf(xi+h/2;yi+bi/2) di=hf(xi+h;yi+ci). Рекуррентная ф-ла для вычисления yi примет вид: yi+1=yi+(ai+2bi+2ci+di)/6
13.Понятие функционала и вариации его аргумента. Примеры. Расстояние между функциями и определение окрестности пространства Ck[a;b]. Пусть дано некоторое множество М ф-ий y(x). Если каждой ф-ии y(x)ϵМ по нек. закону поставлено в соответствие число J, то говорят, что на мн-ве М опред. Функционал J=J[y(x)]; М-обл. оперд. Ф. Пример: Пусть М=С1[a;b]-мн-во всех функций y(x) имеющих непр. y'(x) на [a;b]. Вариацией (превращением) δy аргумента y0(x)ϵM Ф. J=J[y(x)] наз. разность между двумя ф-ми y(x) и y0(x), где y(x)ϵM т.е. δy=y(x)- y0(x). Замечание: Если задано множество k раз непрерывно дифференцируемой на [a;b] ф-ции Ck[a;b], то (δy)'=y'(x)- y0'(x)= δy' … (δy)(k)=y(k)(x)- y0(k(x)= δy(k) Это означает, что производные от вариации ф-ции y0(x) равны вариации производных, т.е. если ф-ция y0(x) получит превращение, то ее первая производная получит превращение δy'=(δy)' … до (k). Говорят, что кривые y=y1(x) и y=y2(x) зад. на [a;b] близки между собой в смысле близости нулевого порядка, если мал |y1(x)- y2(x)| на [a;b]. Геометрически это означает, что кривые на [a;b] близки по ординатам между собой. Говорят, что кривые y=y1(x) и y=y2(x) зад. на [a;b] близки между собой в смысле близости первого порядка, если равны |y1(x)- y2(x)|= |y1'(x)- y2'(x)| на [a;b]. Кривые y=y1(x) и y=y2(x) зад. на [a;b] близки между собой в смысле близости k-ого порядка, если малы величины: |y1(x)- y2(x)|; |y1'(x)- y2'(x)| … |y1(k)(x)- y2(k)(x)| Опр. Расстояние 0-го порядка между кривыми y=y1(x) и y=y2(x) зад. на [a;b] наз. неотрицательно число ρ0= ρ0(y1(x);y2(x))=
14. Непрерывность Ф. Приращение Ф. Линейность Ф. Ф. J[y(x)], определенный в Ck[a;b], наз. непрерывным на y0(x), если для любого числа Ɛ>0, существует ɳ>0, что ρk(y(x);y0(x))< ɳ => |J[y(x)]-J[y0(x)]|<Ɛ, где y(x)ϵCk[a;b]. Это опр. аналогично опр. непрерывности ф-ии y=f(x). Приращение Ф J[y(x)] отвечает приращению δy аргумента y0(x), наз. вел. ∆J=J[y0(x)+ δy]-J[y0(x)]. Ф J[y(x)], определенный в Ck[a;b], наз. непрерывной в y0(x), если Ф. L[Cy(x)], опр. в пространстве Ck[a;b] наз. линейным если он удовл. след. усл.: 1)L[Cy(x)]=CL[y(x)], где CϵR; 2)L[y1(x)+ y2(x)]=L[y1(x)]+L[y2(x)]. Вспомним опред. дифференцируемой ф-ии: Если приращение ф-ии в т. х0 ∆f=f(х0+∆x)-f(х0) мб. Представлено в виде ∆f=A(х0)∆x+β(х0;∆x)∆x, где A(х0) не зависит от ∆x, а β(х0;∆x)->0 при ∆x->0, то ф-я наз. дифференцируемой, а главная линейная часть приращения A(х0)∆x-дифференциал ф-ии и обознач. df. Разделив ∆f на ∆x и переходя к пределу при ∆x->0 получим A(х0)=f '(х0) и => df=f '(х0)∆x
15. Вариация функционала как главная линейная часть приращения и как производная по пар-ру. Если приращение Ф. в т. y0(x)ϵCk[a;b] ∆J=J[y0(x)+δy]-J[y0(x)] можно представить в виде: ∆J=L[y0(x);δy]+β(y0(x); δy)max| δy |, где L[y0(x);δy]-линейный по отношению к δy Ф, β(y0(x); δy)->0 при max| δy |->0, то линейная по отношению к δy часть приращения Ф наз. вариацией Ф и обознач. δy. Тут пример. Через параметр α можно определить и вариацию Ф, но сначала дадим опр. дифференциала ф-ии f(x) через производную по параметру. Рассм. Значение ф-ии f(x+ α∆x) при фиксированных x и ∆x и измен. пра-м α. При α=1 получим приращенное значение ф-ии f(x+ ∆x); При α=0 мы имеем f(x). Нетрудно проверить, что производная по парм. α от f(x+ α∆x) при α=0 диф. f(x) в т. х.
16. Функционал Экстремум Ф-ла на всей области определения наз-ся абсолютным экстремумом. Функции для которых
17. Лемма:Если для каждой непрерывной ф-ии Замечание1:Утверждение Леммы и её док-во не применяется, если на функцию Замечание2:функцию Очевидно, что ф-я удовлетворяет упомянутым выше условиям. Она непрерывна, имеет непрерывные производные до порядка 2n-1, обращается в нуль в точках a и b. И может быть б/м вместе со своими производными за счёт уменьшения множителя k. Замечание3:Аналогично можно док-ть, что ф-я F(x;y) непрерывна в области D плоскости xOy и Т.о. Лемма справедлива для n- кратных интегралов.
18. Пусть ф-я Замечание:Простейшая задача вариационного исчисления состоит в отыскании экстремума функционала (3,2) на множестве всех гладких кривых содержащих заданные точки P1(a;A); P2(b;B) Теорема:Если функционал (3,2) определенный на множестве ф-ий
На кривой y0(x) реализующий экстремум рассматриваемого функц-ла (3,2), явл решением дифф-ого уравнения (3,3) второго порядка. Замечание1:только на удовлетворяющих этим условиям экстремалях может реализоваться экстремум функц-ла, однако, для того, чтобы установить, реализ-ся ли на них в действительности экстремум и притом мах или мин надо иметь достаточные условия экстремума. Замечание2:краевая задача: Замечание3:во многих вариационных задачах существование решения очевидно из физического или геометрического смысла задачи и если решение уравнения Эйлера, удовлетворяющее граничным условиям единственно, то это единственная экстремаль и будет решением, рассматриваемой задачи.
19.
|

 и составим интегральную сумму
и составим интегральную сумму  .
. Предел этой суммы есть опред интерпол
Предел этой суммы есть опред интерпол  .
.



 можно принять интерполяцию многочлен Лагранжа 2й степени проход через точки.
можно принять интерполяцию многочлен Лагранжа 2й степени проход через точки. 
 получим
получим  .
. 
 тогда матожидание:
тогда матожидание:  пусть на (а;в) задана непрерывная ф-я f(x), тогда если x-случайная величина, то и f(x)-случайная велочина причем если x равномерно распределять на (а;в) то и f(x) тоже равномерно распределена на (а;в) т.е. матожидание f(x) будет равно:
пусть на (а;в) задана непрерывная ф-я f(x), тогда если x-случайная величина, то и f(x)-случайная велочина причем если x равномерно распределять на (а;в) то и f(x) тоже равномерно распределена на (а;в) т.е. матожидание f(x) будет равно: 
 с начальным условием
с начальным условием  . Если f(x;y) удовлетворяют всем условиям теорем о существовании и единстве задачи Коши, то существует единственное решение, причем оно является аналитическим в т. X0 и следовательно м.б. представлено в виде ряда Тейлора:
. Если f(x;y) удовлетворяют всем условиям теорем о существовании и единстве задачи Коши, то существует единственное решение, причем оно является аналитическим в т. X0 и следовательно м.б. представлено в виде ряда Тейлора:  p. Первый член ряда опред из начальных условий
p. Первый член ряда опред из начальных условий  Остальные числа ряда находим шаг за шагом путем дифференцирования дифура (*) используют правила дифф неявно заданной ф-ии:
Остальные числа ряда находим шаг за шагом путем дифференцирования дифура (*) используют правила дифф неявно заданной ф-ии: 
 с конечным условием
с конечным условием  для
для  . Интегрирую правую и левую часть можно по отразить (x0;x) получим
. Интегрирую правую и левую часть можно по отразить (x0;x) получим  . Для решения этого уравнения примем метод последовательности приближений. Заменяя неизвестную ф-ю y на y0 получим первое приближение
. Для решения этого уравнения примем метод последовательности приближений. Заменяя неизвестную ф-ю y на y0 получим первое приближение  . Даже подставив вместо y найденное y1 получим второе приближение
. Даже подставив вместо y найденное y1 получим второе приближение  и т.д.
и т.д.  . Геометрическая послед приближений представляет собой кривые, проход через общую точку (x0;y0).
. Геометрическая послед приближений представляет собой кривые, проход через общую точку (x0;y0). . Опр. Расстоянием k-го порядка между ф-ми y1(x) и y2(x) зад. на множ. Сk[a;b], наз. наибольший из максимумов
. Опр. Расстоянием k-го порядка между ф-ми y1(x) и y2(x) зад. на множ. Сk[a;b], наз. наибольший из максимумов  . Опр. Ɛ окрестностью k-го порядка кривой y0(x) и множ. Сk[a;b] наз. совокупность всех кривых y(x) из Сk[a;b] расстояние k-го порядка от которых y0(x)< Ɛ. Зам. Ɛ ок-тью 0-го порядка кривой y0(x) сост. из всех кривых y(x) расположенных в полосе шириной 2Ɛ вокруг кривой y0(x)
. Опр. Ɛ окрестностью k-го порядка кривой y0(x) и множ. Сk[a;b] наз. совокупность всех кривых y(x) из Сk[a;b] расстояние k-го порядка от которых y0(x)< Ɛ. Зам. Ɛ ок-тью 0-го порядка кривой y0(x) сост. из всех кривых y(x) расположенных в полосе шириной 2Ɛ вокруг кривой y0(x) . Тут должен быть прим.
. Тут должен быть прим. . Аналогично для Ф нескольких переменных: f(x1+α∆x1;x2+α∆x2…xn+α∆xn)=
. Аналогично для Ф нескольких переменных: f(x1+α∆x1;x2+α∆x2…xn+α∆xn)=  и для Ф вида J[y(x)] или более сложных, зависящих от неск. неизв. ф-ий или от ФНП можно опред. вариацию как производную от Ф J[y(x)+αδy] по парам. α при α->0, т.е.
и для Ф вида J[y(x)] или более сложных, зависящих от неск. неизв. ф-ий или от ФНП можно опред. вариацию как производную от Ф J[y(x)+αδy] по парам. α при α->0, т.е. 

 заданный ы линейном пространстве Сk[a;b] достигает на прямой y=y0(x) max(min) если найдётся
заданный ы линейном пространстве Сk[a;b] достигает на прямой y=y0(x) max(min) если найдётся  окрестность точки
окрестность точки  , что для всех кривых
, что для всех кривых  из этой окр-ти
из этой окр-ти  -max;
-max;  -min;Необходимое условие экстремума Ф-ла: Если Ф-л
-min;Необходимое условие экстремума Ф-ла: Если Ф-л  .
. будем называть стационарными.
будем называть стационарными.
 , где f(x)-непрерывная на отрезке [а;b] функция, то f(x)=0 на [a;b]
, где f(x)-непрерывная на отрезке [а;b] функция, то f(x)=0 на [a;b]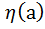 =
=  =0 и
=0 и 

 имеет непрерывные частные производные по всем своим аргументам до 2-го порядка включительно, среди всех функций
имеет непрерывные частные производные по всем своим аргументам до 2-го порядка включительно, среди всех функций  , удовлетворяющие граничным условиям.y(a)=A, y(b)=B (3,1) Найти ту функцию, которая доставляет экстремум фенкционалу
, удовлетворяющие граничным условиям.y(a)=A, y(b)=B (3,1) Найти ту функцию, которая доставляет экстремум фенкционалу  (3,2)
(3,2) (3,3)
(3,3) 

 ;y(a)=A, y(b)=B не всегда имеет решение. А если решение существует, то оно может быть не единственным.
;y(a)=A, y(b)=B не всегда имеет решение. А если решение существует, то оно может быть не единственным.



