Дискретный вариационный ряд
| Номер интервала
i
| Среднее значение интервала

| Относительная частота

| Выборочная
оценка плотности вероятности

| |
| 149,5
| 0,005
| 0,002
| |
| 152,5
|
|
| |
| 155,5
| 0,025
| 0,008
| | Окончание таблицы 7
| |
| 158,5
| 0,035
| 0,012
| |
| 161,5
| 0,105
| 0,035
| |
| 164,5
| 0,19
| 0,063
| |
| 167,5
| 0,195
| 0,065
| |
| 170,5
| 0,19
| 0,063
| |
| 173,5
| 0,105
| 0,035
| |
| 176,5
| 0,075
| 0,025
| |
| 179,5
| 0,04
| 0,013
| |
| 182,5
| 0,015
| 0,005
| |
| 185,5
| 0,015
| 0,005
| |
| 188,5
| 0,005
| 0,002
|
Рис.1
Рис.2
На основании полученных выборочных данных необходимо сделать предположение, что изучаемая величина распределена по некоторому определённому закону. Для того чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты полученных в наблюдениях значений, т.е. находят теоретически сколько раз величина Х должна была принять каждое из наблюдавшихся значений, если она распределена по предполагаемому закону. Для этого находят выравнивающие (теоретические) частоты по формуле:
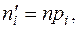 (7) (7)
где n – число испытаний,
 - вероятность наблюдаемого значения - вероятность наблюдаемого значения 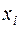 , вычисленная при допущении, что Х имеет предполагаемое распределение. , вычисленная при допущении, что Х имеет предполагаемое распределение.
Эмпирические (полученные из таблицы) и выравнивающие частоты сравнивают, и при небольшом расхождении данных делают заключение о выбранном законе распределения.
Предположим, что случайная величина Х распределена нормально (см. комментарии к задаче № 4). В этом случае выравнивающие частоты находят по формуле:
 (8) (8)
где n -число испытаний,
h -длина частичного интервала,
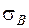 -выборочное среднее квадратичное отклонение, -выборочное среднее квадратичное отклонение,
 ( (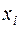 - середина i – го частичного интервала) - середина i – го частичного интервала)
 – функция Лапласа (9) – функция Лапласа (9)
Результаты вычислений отобразим в таблице №8.
Сравнение графиков (рис.2) наглядно показывает близость выравнивающих частот к наблюдавшимся и подтверждает правильность допущения о том, что обследуемый признак распределён нормально.
Таблица 8
Расчёт выравнивающих частот
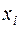
| 
| 
| 
| 
|
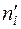
|
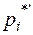
| | 149,5
152,5
155,5
158,5
161,5
164,5
167,5
170,5
173,5
176,5
179,5
182,5
185,5
188,5
| -19,5
-16,5
-13,5
-10,5
-7,05
-4,05
-1,05
1,95
4,95
7,95
10,95
13,95
16,95
19,95
| -3
-2,53
-2,06
-1,59
-1,11
-0,64
-0,17
0,31
0,78
1,25
1,73
2,2
2,67
3,15
| 0,004
0,02
0,048
0,11
0,22
0,33
0,396
0,38
0,3
0,18
0,09
0,04
0,011
0,003
| 0,42
1,55
4,54
10,68
20,37
31,0
37,48
36,0
28,0
17,34
8,44
3,37
1,06
0,26
|
| 0,05
0,01
0,025
0,055
0,1
0,155
0,185
0,18
0,14
0,085
0,04
0,015
0,005
| 
Интервальный вариационный ряд графически изобразим в виде гистограммы (рис.3). На оси Х отложим интервалы длиной h =3, а на оси Y значения  ,расчёт которых представлен в таблице №7. Площадь под гистограммой равна сумме всех относительных частот, т.е. единице. ,расчёт которых представлен в таблице №7. Площадь под гистограммой равна сумме всех относительных частот, т.е. единице.
Графическое изображение вариационных рядов в виде полигона и гистограммы позволяет получать первоначальное представление о закономерностях, имеющих место в совокупности наблюдений.

Рис.3 
3) Найдём числовые характеристики вариационного ряда, используя таблицу №4.
Выборочная средняя ( ): ):

или 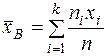 , (10) , (10)
где  - частоты, - частоты,
а  -объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения). -объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения).
В некоторых случаях  удобнее рассчитать с помощью условных вариант. В нашем случае варианты удобнее рассчитать с помощью условных вариант. В нашем случае варианты 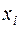 - большие числа, поэтому используем разность: - большие числа, поэтому используем разность:
 (11) (11)
где С – произвольно выбранное число (ложный нуль). В этом случае
 . (12) . (12)
Для изменения значения варианты можно ввести также условные варианты путём использования масштабного множителя:
 , (13) , (13)
где 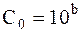 (b выбирается положительным или отрицательным числом). (b выбирается положительным или отрицательным числом).
  . Здесь С – середина 8-го интервала. . Здесь С – середина 8-го интервала.
Выборочная дисперсия ( ): ):
 (14) (14)
 также может быть рассчитана с помощью условных вариант: также может быть рассчитана с помощью условных вариант:
 (15) (15)
 = = 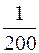 (1*441+0*324+…+1*324)- 1,95²=40,21 (1*441+0*324+…+1*324)- 1,95²=40,21
Среднеквадратическое отклонение:
 = =  (16) (16)
 = =  =6,34 =6,34
Найдем несмещённую оценку дисперсии и среднеквадратического отклонения («исправленную» выборочную дисперсию и среднеквадратическое отклонение) по формулам:
  и и  (17) (17)
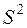 = =  =40,41 и S = =40,41 и S =  6,34=6,36 6,34=6,36
Доверительный интервал для оценки математического ожидания с надёжностью  0,95 определяют по формуле: 0,95 определяют по формуле:
P( - t - t  Ф(t)= Ф(t)=  (18) (18)
Из соотношения Ф(z)=  /2 вычисляют значение функции Лапласа: Ф(z)=0,475. По таблице значений функции Лапласа (Приложение А) находят z =1,96. Таким образом, /2 вычисляют значение функции Лапласа: Ф(z)=0,475. По таблице значений функции Лапласа (Приложение А) находят z =1,96. Таким образом,
168,55-1,96  , ,
167,67< a <169,43.
Доверительный интервал для оценки среднего квадратичного отклонения случайной величины находят по формуле:
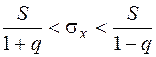 , (19) , (19)
где S – несмещённое значение выборочного среднего квадратичного отклонения;
q – параметр, который находится по таблице (Приложение В) на основе известного объёма выборки n и заданной надёжности оценки  . .
На основании данных значений  =0,95 и n =200 по таблице (Приложение В) можно найти значение q =0,099. Таким образом, =0,95 и n =200 по таблице (Приложение В) можно найти значение q =0,099. Таким образом,
 , ,
5,79 < 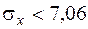
V =  (20) (20)
4) Проведём статистическую проверку гипотезы о нормальном распределении. Нормальный закон распределения имеет два параметра (r =2): математическое ожидание и среднее квадратическое отклонение. По выборочным данным (таблицы 5 и 7) полученные оценки параметров нормального распределения, вычисленные выше:
 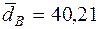 , ,  , S =6,36. , S =6,36.
Для расчёта теоретических частот  используют табличные значения функции Лапласа Ф(z). Алгоритм вычисления используют табличные значения функции Лапласа Ф(z). Алгоритм вычисления  состоит в следующем: состоит в следующем:
- по нормированным значениям случайной величины Z находят значения Ф(z), а затем 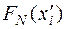 : :
 , ,  =0,5+ Ф( =0,5+ Ф(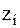 ). ).
Например,
 ; ; 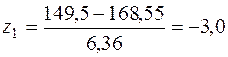 ; Ф (-3,0) = -0,4987; ; Ф (-3,0) = -0,4987;
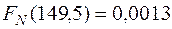 ; ;
- далее вычисляют вероятности  = P ( = P ( ; ;
- находят числа  , и если некоторое , и если некоторое  <5, то соответствующие группы объединяются с соседними. <5, то соответствующие группы объединяются с соседними.
Результаты вычисления  , ,  , и , и 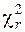 приведены в таблице 9. приведены в таблице 9.
По формуле
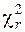 = =  (21) (21)
можно сделать проверку расчетов.

По таблице (приложения Г) можно найти число 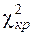 по схеме: для уровня значимости α;=0,05 и числа степеней свободы l=k-r-1 =9-2-1=6 по схеме: для уровня значимости α;=0,05 и числа степеней свободы l=k-r-1 =9-2-1=6  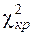 =12,6. Следовательно, критическая область - (12,6; =12,6. Следовательно, критическая область - (12,6;  ). Величина ). Величина  =15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается. =15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.
При α;=0,1 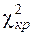 =10,6. Критическая область - (10,6; =10,6. Критическая область - (10,6;  ). Величина ). Величина  =15,61 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается. =15,61 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
При α;=0,01 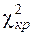 =16,8, (16,8; =16,8, (16,8;  ). В этом случае нет оснований отвергать гипотезу о нормальном законе распределения. ). В этом случае нет оснований отвергать гипотезу о нормальном законе распределения.
Таблица 9
Определение 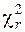
| i
| 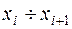
| 
| Ф ( ) )
| 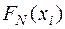
| 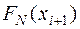 
|  
|  
| 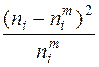 
| |
| 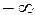  149,5
149,5
|
| -0,500
| 0,000
| 0,0013
| 0,0013
| 0,26
| -
| |
| 149,5 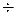 152,5
152,5
|
| -0,449
| 0,0013
| 0,0059
| 0,0046
| 0,92
| -
| |
| 152,5 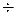 155,5
155,5
|
| -0,494
| 0,0059
| 0,02
| 0,014
| 2,8
| -
| |
| 155,5 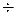 158,5
158,5
|
| -0,48
| 0,02
| 0,057
| 0,037
| 7,4
| 2,54
| |
| 158,5 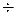 161,5
161,5
|
| -0,44
| 0,057
| 0,134
| 0,077
| 15,4
| 4,58
| |
| 161,5 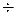 164,5
164,5
|
| -0,37
| 0,134
| 0,26
| 0,126
| 25,2
| 0,7
| |
| 164,5 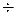 167,5
167,5
|
| -0,24
| 0,26
| 0,433
| 0,1725
| 34,5
| 0,36
| |
| 167,5 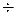 170,5
170,5
|
| -0,07
| 0,433
| 0,62
| 0,188
| 37,6
| 0,06
| |
| 170,5 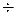 173,5
173,5
|
| 0,12
| 0,62
| 0,78
| 0,16
|
| 1,125
| |
| 173,5 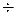 176,5
176,5
|
| 0,28
| 0,78
| 0,89
| 0,11
|
| 0,045
| |
| 176,5 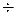 179,5
179,5
|
| 0,39
| 0,89
| 0,96
| 0,07
|
| 0,071
| |
| 179,5 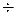 182,5
182,5
|
| 0,46
| 0,96
| 0,99
| 0,03
|
| 6,125
| |
| 182,5 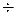 185,5
185,5
|
| 0,49
| 0,99
| 0,996
| 0,006
| 1,2
| -
| |
| 185,5  188,5
188,5
|
| 0,496
| 0,996
| 0,999
| 0,003
| 0,6
| -
| |
| 188,5 

|
| 0,5
| 0,999
| 1,0
| 0,001
| 0,2
| -
|   ,0000 ,0000 
2 часть
1) Данные таблицы 3 сгруппируем в корреляционную таблицу 10.
2) Строим в системе координат множество, состоящее из 200 экспериментальных точек (рисунок 4).
По расположению точек делаем заключение о том, что экономико-математическую модель можно искать в виде 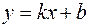 . .
3) Найдём выборочные уравнения линейной регрессии.
Для упрощения расчётов разобьём случайные величины на интервалы и выберем средние значения. Для величины Х указанные действия были выполнены в 1 части задания.
Таблица 10
Корреляционная таблица

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y/X
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Продолжение таблицы 10
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
Рис.4
Для случайной величины Y, используя (1), получим h =2, число интервалов равно 13. Результаты внесём в таблицу со сгруппированными данными №11.
Находим средние значения  , по формулам: , по формулам:
 , (22) , (22)
 , (23) , (23)
 , (24) , (24)
 . (25) . (25)
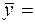 


 149,5*86+155,5(82+…+90)+…+188,5*104=2986101 149,5*86+155,5(82+…+90)+…+188,5*104=2986101
Используя формулы:
 , (26) , (26)
 , (27) , (27)
получим
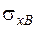 = = 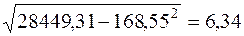 , ,  = = 
Таблица 11
Сгруппированные данные выборки
| №
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| XY
| 149,5
| 152,5
| 155,5
| 158,5
| 161,5
| 164,5
| 167,5170,5173,5
| 170,5
| 173,5
| 176,5
| 179,5
| 182,5
| 185,5
| 188,5
| 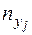
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) Вычисляем выборочный коэффициент корреляции  по формуле: по формуле:
 . (28) . (28)
 = = 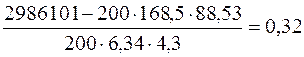
Принято считать, что если 0,1<  <0,3 – связь слабая, если 0,3< <0,3 – связь слабая, если 0,3<  <0,5 – связь умеренная, если 0,5< <0,5 – связь умеренная, если 0,5<  <0,7 – связь заметная, если 0,7< <0,7 – связь заметная, если 0,7<  <0,9 – связь высокая, если 0,9< <0,9 – связь высокая, если 0,9<  <0,99 – связь весьма высокая. <0,99 – связь весьма высокая.
Для данного примера связь между X и Y умеренная.
Затем получают выборочное уравнение линейной регрессии Y на X в виде:
 (29) (29)
и выборочное уравнение линейной регрессии X на Y:
 . (30) . (30)
 и и

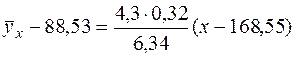 или или

Вычисления сумм рекомендуем проводить с помощью пакетов прикладных математических программ (сегодня их существует много).

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
|
РЕВМАТИЧЕСКИЕ БОЛЕЗНИ Ревматические болезни(или диффузные болезни соединительно ткани(ДБСТ))— это группа заболеваний, характеризующихся первичным системным поражением соединительной ткани в связи с нарушением иммунного гомеостаза...
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
|
|
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
Понятие и структура педагогической техники Педагогическая техника представляет собой важнейший инструмент педагогической технологии, поскольку обеспечивает учителю и воспитателю возможность добиться гармонии между содержанием профессиональной деятельности и ее внешним проявлением...
Репродуктивное здоровье, как составляющая часть здоровья человека и общества
Репродуктивное здоровье – это состояние полного физического, умственного и социального благополучия при отсутствии заболеваний репродуктивной системы на всех этапах жизни человека...
|
|






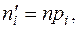 (7)
(7) - вероятность наблюдаемого значения
- вероятность наблюдаемого значения 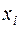 , вычисленная при допущении, что Х имеет предполагаемое распределение.
, вычисленная при допущении, что Х имеет предполагаемое распределение. (8)
(8)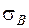 -выборочное среднее квадратичное отклонение,
-выборочное среднее квадратичное отклонение, (
( – функция Лапласа (9)
– функция Лапласа (9)


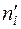
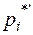

 ,расчёт которых представлен в таблице №7. Площадь под гистограммой равна сумме всех относительных частот, т.е. единице.
,расчёт которых представлен в таблице №7. Площадь под гистограммой равна сумме всех относительных частот, т.е. единице.

 ):
):
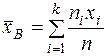 , (10)
, (10) - частоты,
- частоты, -объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения).
-объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения). (11)
(11) . (12)
. (12) , (13)
, (13)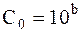 (b выбирается положительным или отрицательным числом).
(b выбирается положительным или отрицательным числом).
 . Здесь С – середина 8-го интервала.
. Здесь С – середина 8-го интервала. ):
): (14)
(14) (15)
(15) =
= 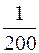 (1*441+0*324+…+1*324)- 1,95²=40,21
(1*441+0*324+…+1*324)- 1,95²=40,21 =
=  (16)
(16) =
=  =6,34
=6,34 и
и  (17)
(17)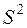 =
=  =40,41 и S =
=40,41 и S =  6,34=6,36
6,34=6,36 0,95 определяют по формуле:
0,95 определяют по формуле: - t
- t  Ф(t)=
Ф(t)=  (18)
(18) ,
,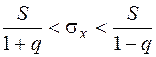 , (19)
, (19) ,
,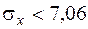
 (20)
(20)
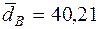 ,
,  , S =6,36.
, S =6,36. используют табличные значения функции Лапласа Ф(z). Алгоритм вычисления
используют табличные значения функции Лапласа Ф(z). Алгоритм вычисления  :
: ,
,  =0,5+ Ф(
=0,5+ Ф( ).
). ;
; 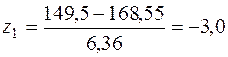 ; Ф (-3,0) = -0,4987;
; Ф (-3,0) = -0,4987;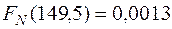 ;
; ;
; , и если некоторое
, и если некоторое  <5, то соответствующие группы объединяются с соседними.
<5, то соответствующие группы объединяются с соседними.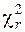 приведены в таблице 9.
приведены в таблице 9. (21)
(21)
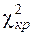 по схеме: для уровня значимости α;=0,05 и числа степеней свободы l=k-r-1 =9-2-1=6
по схеме: для уровня значимости α;=0,05 и числа степеней свободы l=k-r-1 =9-2-1=6 
 ). Величина
). Величина  =15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.
=15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.

 )
)
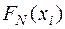
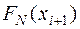




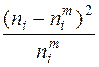
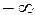
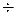 149,5
149,5

 ,0000
,0000 
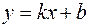 .
.


 , по формулам:
, по формулам: , (22)
, (22) , (23)
, (23) , (24)
, (24) . (25)
. (25)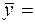



 149,5*86+155,5(82+…+90)+…+188,5*104=2986101
149,5*86+155,5(82+…+90)+…+188,5*104=2986101 , (26)
, (26) , (27)
, (27)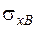 =
= 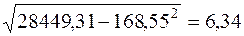 ,
,  =
= 
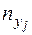

 по формуле:
по формуле: . (28)
. (28)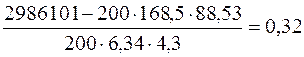
 (29)
(29) . (30)
. (30) и
и
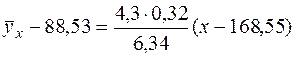 или
или



