Анализ способа, включающего арифметическую формулуВыше мы рассмотрели двухплоскостную структуру, образованную связью особого содержания и фиксирующей его формулы D + D = О (О — D = D). Теперь дети не допускали тех ошибок в составлении формулы, которые были для них характерные, когда они действовали на основании отдельно взятых отношений «части — целое» и равенства. Какова будет структура способа, включающего арифметические операции? Следуя принятому методу, мы будем идти от минимального состава способа, постепенно включая в него новые необходимые элементы. 1. Прежде всего мы должны посмотреть, не достаточна ли полученная выше структура для полноценного применения арифметических операций. Это значит, что в таком случае числовая формула может быть введена в нее формально (по формальному правилу замещения буквенных значков цифрами) и здесь не потребуется дополнения способа специфическими операциями, задающими новые элементы содержания, или процесса переходя к новой плоскости замещения. Конец страницы 371 ¯ Начало страницы 372 ¯ Опыты, проводимые с детьми, прошедшими предыдущие серии обучения (4г. 11 мес.), заключались в следующем: действуя с объектами отношений «целое — части» и равенства так, как их обучали раньше, дети составляли формулу D + D = О, или О — D = D. После этого экспериментатор указывал, что одна часть ((или в одной части), например, у нас будет 3, а другая 2. Под значками выкладывались карточки с соответствующими цифрами, и нужно было узнать, сколько будет составлять целое. Показывался способ построения числовой формулы на основе формулы D + D = О (или О — D = D): D + D = О 3 + 2=... Дети должны были затем сами составлять таким же образом числовую формулу и получать ответ (напомним, что дополнение числовой формулы последним числом — числом ответа — было усвоено этими испытуемыми еще в первых сериях обучения). Такое обучение проводилось в течение пяти занятий (каждое по 20 минут). Результаты. Дети могут воспроизвести вслед за экспериментатором показанные им действия. При самостоятельном же их выполнении они начинают допускать следующие ошиб- t< ки: а) выложив соответствующие цифры, испытуемые не дополняют формулу числом ответа; б) испытуемые смешивают знаки двух формул, например: построив формулу 3 + 2 =, вместо последнего числа подставляют в нее значок D (3 + 2 = О) и зачитывают ее так: «К трем прибавить два равно целое». Одна девочка (Алла А., 4 г. 11 мес.) при построении формулы D -f- D = О вместо значка О поставила цифру 3 (воспроизведя число ответа из предыдущего задания); в) у ряда испытуемых встречались такие ошибки: 3 — 2 = 2, 5 — 3 = 3. Попробуем интерпретировать эти эмпирические результаты и сформулировать гипотезу об их причинах, которая должна быть проверена при последующих сериях обучения. Факт смешения знаков формул разных плоскостей может быть выражением того, что при данном обучении детям не задается специального содержания (или операций) числового замещения. Ошибки типа 3 — 2=2, 5 — 3 = 3 обусловлены также уподоблением числовой формулы фор- Конец страницы 372 ¯ Начало страницы 373 ¯ муле О — D = D; в формуле О — D = D знак D обозначает любую из частей целого" и не фиксирует их различия. В формуле 3 — 2=1 и 2 и 1 должны выступать как обозначение частей целого, но частей, представленных разными величинами. В связи с этим возникает вопрос, не приведет ли отработка родовидовых отношений к преодолению такого типа трудностей. Интерпретация ошибки, приведенной нами в пункте а, будет дана ниже. Итак, учитывая описанные особенности действия детей и их интерпретацию, мы должны ввести в способ новые элементы, обеспечивающие числовое замещение. По сути дела, мы здесь подошли к вопросу об отношении арифметических действий и счета, к вопросу о том, как генетически связаны эти два способа, какие элементы счета и в какой форме должны быть включены в арифметический способ. 2. То особое отношение совокупностей, которое фиксируется арифметической формулой, уже выделено в способе посредством действий с отношениями равенства и «целое — части» и их знаковой фиксации. Поэтому возникает вопрос: не будет ли достаточно для введения числовой формулы в данный способ дополнить его лишь связью «предметная совокупность — число», т. е. ввести числа как замещающие предметные совокупности пересчитанных единиц? Теперь к предыдущему обучению добавляется следующее: помимо карточек с цифрами, дети выкладывают соответствующие заданным числам предметные совокупности и, осуществив пересчет или отсчет, получают число ответа. В этих условиях испытуемые выполняют пересчет или отсчет, при составлении формулы не допускают смещения знаков разных плоскостей, но не могут: а) перейти к использованию арифметической формулы вне действия с предметной совокупностью; когда после шести занятий мы сняли выкладывание совокупностей, дети вновь стали обнаруживать все те ошибки, которые были описаны нами в пункте 1; б) соотнести числовые операции с формулой D + D = О (О — D = D) и с предметной ситуацией, соответствующей действию с отношением «целое — части» и отношением равенства: когда мы, указывая на предметные модели, просим детей ответить на вопросы «целое — сколько»?, Конец страницы 373 ¯ Начало страницы 374 ¯ «часть — сколько?» или задаем эти же вопросы, относя их к формуле D + D = О, дети не могут ответить правильно. Точно так же они не отвечают правильно, когда мы, указывая на знаки формулы 3 + 2 = 5, спрашиваем: «3 — это — что, целое или часть?», «5 — это часть или целое?» и т. п. Итак, при введении отношения «предметный пересчет — число» (которое задавалось в виде связки операций) дети стали правильно подставлять числа в формулу и получать число ответа, но эти операции не были связаны с остальными элементами (плоскостями) нашего способа и не приводили к такому использованию арифметической формулы, которое позволило бы не выполнять действие с единицами предметных совокупностей. 3. Если в предыдущей серии мы ввели счет лишь в форме связки операций (предметная операция — число), то теперь мы попробуем использовать действие счета: связка операций (предметная операция — число) берется как средство опосредованного уравнивания. Поскольку при арифметическом действии мы имеем дело с задачей объединения — разъединения совокупностей при сопоставлении двух ситуаций, то для введения сюда действия счета мы должны связать задачу объединения — разъединения совокупностей и задачу опосредованного уравнивания. Как и в предыдущей серии, помимо моделей «целое — части», дети выкладывают соответствующие заданным числам предметные совокупности (схема 33).
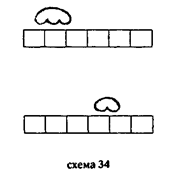
В стороне либо на другом столике лежало некоторое число таких же предметов (палочек или пуговиц и т. п.). Составлялись формулы: 3 + 2 = Обе группы предметов сдвигались: «части соединили — Конец страницы 374 ¯ Начало страницы 375 ¯ получили целое»; экспериментатор просил принести со столика столько предметов, чтобы их число было равно этому целому. В другом варианте обучения бумажные полоски, моделирующие «целое — части», были расчерчены на равные отрезки, а в стороне лежали разные таким же образом расчерченные полоски. Дети должны были подобрать из них полоску, равную целому, получаемому при соединении частей. Затем дети пересчитывали предметы из заданных совокупностей и по полученному числу должны были отобрать нужную полоску. В результате этого обучения мы не получили никаких сдвигов по сравнению с предыдущими сериями. Дети действовали либо с моделями целого и частей, но не строили при этом правильно числовую формулу, либо пересчитывали предметные совокупности, составляли формулу, но не соотносили ее с остальными плоскостями действия. 4. Не удалось преодолеть эти трудности и при таком обучении, когда пересчет осуществлялся непосредственно на полосках, моделирующих целое и части. Когда дети выполняли пересчет, полоски не выступали для них как объекты отношений «целое — части» и равенства (и они не соотносили числовую формулу с содержанием, выраженным этими отношениями); когда же испытуемые действовали с полосками как объектами этих отношений, они не могли правильно составить формулу или соотнести ее с отношениями равенства и «целое — части» и с формулой D + D = О. Итак, условия, использованные в предшествующем обучении (а именно: непосредственное приписывание объектам-моделям числовых значений; введение, помимо действия с моделями, пересчета реальных предметов; наконец, применение таких модельных объектов, к которым могла быть приложена операция присчета, когда испытуемые действовали с полосочками, расчерченными на равные отрезки), не обеспечили правильного составления детьми арифметической формулы. 5. Все это заставило предположить, что здесь необходимо ввести новую плоскость моделей и операций, которая обеспечивала бы переход от объектов отношений равенства и «целое — части» к величинам. Мы вводим в обучение особый объект — длинную полоску, расчерченную на равные отрезки («линеечка»). Испытуемые приклады- Конец страницы 375 ¯ Начало страницы 376 ¯ вают объект «целое» или «части» к линеечке, отсчитывают на ней число квадратиков («окошек») свответвенио числовым значениям заданных объектов, отмечают конец отсчета палочкой, пересчитывают все квадратики до отметки и, получив число, отбирают на другом столике нужную полоску. Вот пример такого обучения. Экспериментатор, выкладывает две полоски с окошками и говорит: что это две части, в одной части 3 окошечка, а а другой 2. Нужно определить, какую взять полоску для целого. Испытуемый соединяет обе полоски и прикладывает их к линейке, строит знаковые формулы D + D= О 3 + 2 = возвращается к полоскам и линейке: «В одной части 3 (считает на линейке: 1, 2, 3 — держит палец на последнем делении), в другой 2 (показывает на полоску 1, 2 и считает на линейке: 1, 2 — держит палец или палочку в конце и, возвращаясь к началу, пресчитывает: 1, 2, 3, 4, 5)». Затем испытуемый ставит цифру в числовую строчку и подбирает соответствующую целую полоску. Аналогичные действия выполняли испытуемые и в случае расчленения целого на части. Затем то же самое проделывается вторично, но уже с полосками без окошек, а потом и без прикладывания полосок к линейке. Одна испытуемая при этом, например вначале, как бы рисовала пальцем полоски над линейкой (схема 34): «Одна часть 3 (и рисует на столе), другая 2 (также «рисует»)»:
После же одного-двух занятий дети стали составлять арифметическую формулу и получать число ответа, не вы- Конец страницы 376 ¯ Начало страницы 377 ¯ полная пересчет на линейке,а используя усвоенную ранее таблицу сложения — вычитания или обращаясь к предложенной им экспериментатором табличке. При этом дети всегда могли ответить правильно на вопросы о связи арифметической формулы с отношениями «целое — части» и равенства («3 — это что?», «целое — сколько?» и т. п.). Как мы видим, введение действия с «линейкой», когда объекты целое — части непосредственно прикладывались к «линейке», выступая при этом одновременно и как объекты целое — части и как величины, обеспечило связь объектов и операций этих разных плоскостей действий. Итак, правильное построение арифметической формулы оказалось возможным при таком способе, когда одни и те же объекты выступали как объекты трех разных систем: отношения равенства, отношения «целое — части» и счета (при этом отношение равенства и счет включались в способ как действия, а отношение «целое — части» — как совокупность oпераций). Это потребовало такой учебной задачи, которая обеспечивала введение трех типов моделей и операций с ними (модели «целое — части», модели отношения равенства, модели объекта пересчета — «ли-•яеечка») и построение такого особого действия, включающего эти три типа объектов и операций, причем таким образом, чтобы одни и те же объекты использовались (рассматривались) во всех этих трех значениях. Заметим, что арифметическая формула является примером специфического знакового замещения, которое в отличие от других типов заместителей (предметных, символических и т. п.), всегда фиксирует синтез разного типа содержаний. А из этого следует, что учебная задача, соответствующая усвоению такого содержания, является искусственной: в том смысле, что она не существовала вне обучения как определенная сложившаяся конкретная деятельность с определенными конкретными предметами, а конструируется специально в целях обучения. Конец страницы 377 ¯ Начало страницы 378 ¯ H. Г. Алексеев
|