ТЕОРИЯ ФРАКТАЛОВ

ПРЕДПОСЫЛКИ ВОЗНИКНОВЕНИЯ

Теория фракталов имеет совсем небольшой возраст. Она появилась в конце шестидесятых годов на стыке математики, информатики, лингвистики и биологии. В то время компьютеры все больше проникали в жизнь людей, ученые начинали применять их в своих исследованиях, росло число пользователей вычислительных машин. Для массового использования компьютеров необходимо стало облегчить процесс общения человека с машиной. Если в самом начале компьютерной эры немногочисленные программисты-пользователи самоотверженно вводили команды в машинных кодах и получали результаты в виде бесконечных лент бумаги, то при массовом и загруженном режиме использования компьютеров возникла необходимость в изобретении такого языка программирования, который был бы понятен для машины, и в то же время, был бы прост в изучении и применении. То есть пользователю требовалось бы ввести только одну команду, а компьютер разложил бы ее на более простые, и выполнил бы уже их. Чтобы облегчить написание трансляторов, на стыке информатики и лингвистики возникла теория фракталов, позволяющая строго задавать взаимоотношения между алгоритмическими языками. А датский математик и биолог А. Линденмеер придумал в 1968 году одну такую грамматику, названную им L-системой, которая, как он полагал, моделирует также рост живых организмов, в особенности образование кустов и веток у растений.

Вот как выглядит его модель. Задают алфавит - произвольный набор символов. Выделяют одно, начальное слово, называемое аксиомой, - можно считать, что оно соответствует исходному состоянию организма – зародышу. А потом описывают правила замены каждого символа алфавита определенным набором символов, то есть задают закон развития зародыша. Действуют правила так: прочитываем по порядку каждый символ аксиомы и заменяем его на слово, указанное в правиле замены.

Таким образом, прочитав аксиому один раз, мы получаем новую строку символов, к которой снова применяем ту же процедуру. Шаг за шагом возникает все более длинная строка – каждый из таких шагов можно считать одной из последовательных стадий развития «организма». Ограничив число шагов, определяют, когда развития считается законченным.

ВОЗНИКНОВЕНИЕ ТЕОРИИ ФРАКТАЛОВ

Отцом фракталов по праву можно считать Бенуа Мандельброта. Мандельброт является изобретателем термина «фрактал». Мандельброт писал: «Я придумал слово «фрактал», взяв за основу латинское прилагательное «fractus», означающее нерегулярный, рекурсивный, фрагментный». Первое определение фракталам также дал Б. Мандельброт:

Фрактал – самоподобная структура, чье изображение не зависит от масштаба. Это рекурсивная модель, каждая часть которой повторяет в своем развитии развитие всей модели в целом.

На сегодняшний день существует много различных математических моделей фракталов. Отличительная особенность каждой из них является то, что в их основе лежит какая-либо рекурсивная функция, например: x_i=f(x_i-1). С применением ЭВМ у исследователей появилась возможность получать графические изображения фракталов. Простейшие модели не требуют больших вычислений и их можно реализовать прямо на уроке информатики, тогда как иные модели настолько требовательны к мощности компьютера, что их реализация осуществляется с применением суперЭВМ. Кстати, в США изучением фрактальных моделей занимается Национальных Центр Приложений для Суперкомпьютеров (NCSA). В данной работе мы хотим показать только несколько моделей фракталов, которые нам удалось получить.

 

1. Модель Мандельброта.

 

Бенуа Мандельброт предложил модель фрактала, которая уже стала классической и часто используется для демонстрации как типичного примера самого фрактала, так и для демонстрации красоты фракталов, которая также привлекает исследователей, художников, просто интересующихся людей.

Математическое описание модели следующее: на комплексной плоскости в неком интервале для каждой точки с вычисляется рекурсивная функция Z=Z²+c. Казалось бы, что такого особенного в этой функции? Но после N повторений данной процедуры вычисления координат точек, на комплексной плоскости появляется удивительно красивая фигура, чем-то напоминающая грушу.

В модели Мандельброта изменяющимся фактором является начальная точка с, а параметр z, является зависимым. Поэтому для построения фрактала Мандельброта существует правило: начальное значение z равно нулю ( z=0 )! Это ограничение вводится для того, чтобы первая производная от функции z в начальной точке была равна нулю. А это означает, что в начальной точке функция имеет минимум, и в дальнейшем она будет принимать только большие значения.

 

 

 

Мы хотим заметить, что если рекурсивная формула фрактала имеет другой вид, то тогда следует выбирать другое значение начальной точки для параметра Z. Например, если формула имеет вид z=z²+z+c, то начальная точка будет равна:

2*z+1=0 Þ z= -1/2.

 

 

В данной работе мы имеем возможность привести изображения фракталов, которые были построены в NCSA. Мы получили файлы с изображениями через сеть Internet.

 

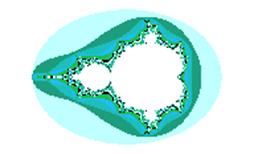
Рис.1 Фрактал Мандельброта

 

 

Вам уже известна математическая модель фрактала Мандельброта. Теперь мы покажем, как она реализуется графически. Начальная точка модели равна нулю. Графически она соответствует центру тела “груши”. Через N шагов заполнятся все тело груши и в том месте, где закончилась последняя итерация, начинает образовываться «голова» фрактала. «Голова» фрактала будет ровно в четыре раза меньше тела, так как математическая формула фрактала представляет из себя квадратный полином. Затем опять через N итераций у «тела» начинает образовываться «почка» (справа и слева от «тела»). И так далее. Чем больше задано числе итераций N, тем более детальным получится изображение фрактала, тем больше будет у него различных отростков. Схематическое изображение стадий роста фрактала Мандельброта представлено на рис.2:

 

Рис.2 Схема образования фрактала Мандельброта

 

Из рисунков 1 и 2 видно, что каждое последующее образование на «теле» точно повторяет в своем строении само тело. Это и есть отличительная черта того, что данная модель является фракталом.

 

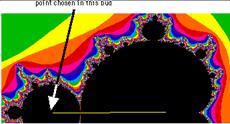
На следующих рисунках показано, как будет изменяться положение точки, соответствующей параметру z, при различном начальном положении точки c.

А) Начальная точка в «теле» Б) Начальная точка в «голове»

 

 

В) Начальная точка в «почке» Г) Начальная точка в «почке» второго уровня

 

Д) Начальная точка в «почке» третьего уровня

 

Из рисунков А - Д хорошо видно, как с каждым шагом все более усложняется структура фрактала и у параметра z все более сложная траектория.

 

 

Ограничения на модель Мандельброта: существует доказательство, что в модели Мандельброта |z|<=2 и |c|<=2.

 

 

2. Модель Джулии (Julia set)

 

Модель фрактала Джулии имеет то же уравнение, что и модель Мандельброта: Z=Z²+c, только здесь переменным параметром является не c, a z.

Соответственно, меняется вся структура фрактала, так как теперь на начальное положение не накладывается никаких ограничений. Между моделями Мандельброта и Джулии существует такое различие: если модель Мандельброта является статической (так как z начальное всегда равно нулю), то модель Джулии является динамической моделью фрактала. На рис. 4 показано графическое представление фрактала Джулии.

 

 

Рис. 4 Модель Джулии

 

 

Как видно из рисунка фрактала, он симметричную относительно центральной точки форму, тогда как фрактал Мандельброта имеет форму, симметричную относительно оси.

 

3. Ковер Серпинского

 

Ковер Серпинского считается еще одной моделью фрактала. Строится он следующим образом: берется квадрат, делится на девять квадратов, вырезается центральный квадрат. Затем с каждым из восьми оставшихся квадратов проделывается подобная процедура. И так до бесконечности. В результате вместо целого квадрата мы получаем ковер со своеобразным симметричным рисунком. Впервые данную модель предложил математик Серпинский, в честь которого он и получил свое название. Пример ковра Серпинского можно увидеть на рис. 4d.

 

 

Рис.4 Построение ковра Серпинского

 

 

4. Кривая Коха

 

В начале ХХ века математики искали такие кривые, которые ни в одной точке не имеют касательной. Это означало, что кривая резко меняет свое направление, и притом с колоссально большой скоростью (производная равна бесконечности). Поиски данных кривых были вызваны не просто праздным интересом математиков. Дело в том, что в начале ХХ века очень бурно развивалась квантовая механика. Исследователь М.Броун зарисовал траекторию движения взвешенных частиц в воде и объяснил это явление так: беспорядочно движущиеся атомы жидкости ударяются о взвешенные частицы и тем самым приводят их в движение. После такого объяснения броуновского движения перед учеными встала задача найти такую кривую, которая бы наилучшим образом аппроксимировала движение броуновских частиц. Для этого кривая должна была отвечать следующим свойствам: не иметь касательной ни в одной точке. Математик Кох предложил одну такую кривую. Мы не будем вдаваться в объяснения правила ее построения, а просто приведем ее изображение, из которого все станет ясно (рис.5).

 

Рис.5 Этапы построения кривой Коха

 

Кривая Коха является еще одним примером фрактала, так как каждая ее часть является уменьшенным изображением всей кривой.

 

 

6. Графические изображения различных фракталов

 

 

В данном пункте мы решили поместить графические изображения различных фракталов, которые мы получили из сети Internet. К сожалению, мы не смогли найти математическое описание этих фракталов, но для того, чтобы понять их красоту, достаточно только рисунков.

 

 

Рис. 6 Примеры графического представления фракталов