Конечные разности. Пусть известны значения некоторой функции  для равноотстоящих значений аргумента
для равноотстоящих значений аргумента 
 . Конечными разностями первого порядка называются следующие величины:
. Конечными разностями первого порядка называются следующие величины:
 ;
;  ; …;
; …;  ; ….
; ….
Aналогично определяются конечные разности второго порядка:
 ;
;  ; …;
; …;  ; …
; …
и т.д.
Конечные разности 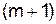 -го порядка выражаем через конечные разности
-го порядка выражаем через конечные разности  -го порядка:
-го порядка:  ;
; 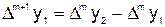 ; …;
; …;  ; ….
; ….
Вычисление конечных разностей можно оформить в виде
табл. 7.1, которая называется диагональной таблицей конечных разностей.
Таблица 7.1
Первая интерполяционная формула Ньютона. Интерполяционный полином Ньютона – форма записи интерполяционного полинома Pn(x), которая допускает уточнения результатов интерполирования последовательным прибавлением новых узлов.
Первая интерполяционная формула Ньютона имеет вид
 ,
,
где  .
.
Формула используется для интерполирования в точках 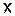 , близких к началу таблицы
, близких к началу таблицы  , поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей.
, поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей.
Погрешность первой интерполяционной формулы Ньютона записывается в виде
 ,
,
где  – некоторая точка интервала, содержащего узлы интерполяции.
– некоторая точка интервала, содержащего узлы интерполяции.
Вторая интерполяционная формула Ньютона. Пусть точка интерполирования 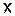 лежит вблизи конечной точки таблицы
лежит вблизи конечной точки таблицы  . В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона
. В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона
 ,
,
где  .
.
Вторая интерполяционная формула Ньютона содержит конечные разности, расположенные в нижней косой строке таблицы конечных разностей.
Погрешность второй формулы
 ,
,
где  – некоторая точка интервала, содержащего узлы интерполяции
– некоторая точка интервала, содержащего узлы интерполяции 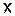 .
.
Интерполяционная формула Гаусса. Пусть точка интерполирования 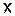 лежит в середине таблицы между узлами интерполяции
лежит в середине таблицы между узлами интерполяции  и
и 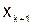 , т.е.
, т.е.  . В этом случае для интерполирования применяется интерполяционная формула Гаусса
. В этом случае для интерполирования применяется интерполяционная формула Гаусса


 ,
,
где  ;
;  – целая часть числа
– целая часть числа  .
.
Погрешность интерполяционной формулы Гаусса имеет вид
 ,
,
где  – некоторая точка интервала, содержащего узлы интерполирования.
– некоторая точка интервала, содержащего узлы интерполирования.
Численное дифференцирование. Пусть функция  задана таблицей своих значений
задана таблицей своих значений 
 . Требуется вычислить производную в некоторой точке
. Требуется вычислить производную в некоторой точке 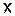 .
.
Пусть для определенности точка 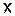 находится в начале таблицы. Построим интерполяционный многочлен по первой формуле Ньютона
находится в начале таблицы. Построим интерполяционный многочлен по первой формуле Ньютона

 ,
,
где  .
.
Производную  приближённо можно вычислить следующим образом:
приближённо можно вычислить следующим образом:
 ,
,
т.е.
 Если требуется найти производную в точке
Если требуется найти производную в точке  , лежащей в середине или в конце таблицы, то формулу для её вычисления получаем, исходя из формулы Гаусса или второй интерполяционной формулы Ньютона.
, лежащей в середине или в конце таблицы, то формулу для её вычисления получаем, исходя из формулы Гаусса или второй интерполяционной формулы Ньютона.
Обратное интерполирование. Задача обратного интерполирования заключается в определении по заданному значению функции  , соответствующего значения
, соответствующего значения  . Если
. Если  – монотонная непрерывная функция на интервале
– монотонная непрерывная функция на интервале  , причем
, причем  , то функция
, то функция  в этом случае имеет обратную функцию.
в этом случае имеет обратную функцию.
Пусть задана функция  :
:
Для многочлена Лагранжа нужно просто перевернуть таблицу:
 .
.
Рассмотрим случай равноотстоящих узлов. Для определенности полагаем, что  содержится между
содержится между  и
и  (для 1-й формулы Ньютона). Этот метод называется методом последовательных приближений:
(для 1-й формулы Ньютона). Этот метод называется методом последовательных приближений:
 .
.
Используем метод итерации. Для этого необходимо уравнение привести к виду  :
:
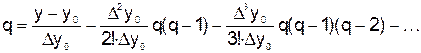 .
.
После приведения уравнения к виду, пригодному для метода итерации, в качестве начального приближения выбираем
 .
.
Доказано, что при 
 . В случае получения расходящегося процесса необходимо уменьшить h. Продолжая процесс итерации, получаем
. В случае получения расходящегося процесса необходимо уменьшить h. Продолжая процесс итерации, получаем

 .
.
Процесс итерации на практике продолжается до тех пор, пока не установятся цифры, соответствующие требуемой точности:

 .
.
Для нахождения корня уравнения  методом обратной интерполяции нужно рассмотреть функцию
методом обратной интерполяции нужно рассмотреть функцию  и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.
и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.

 для равноотстоящих значений аргумента
для равноотстоящих значений аргумента 
 . Конечными разностями первого порядка называются следующие величины:
. Конечными разностями первого порядка называются следующие величины: ;
;  ; …;
; …;  ; ….
; …. ;
;  ; …;
; …;  ; …
; …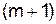 -го порядка выражаем через конечные разности
-го порядка выражаем через конечные разности  -го порядка:
-го порядка:  ;
; 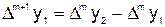 ; …;
; …;  ; ….
; ….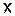
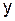








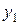

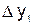
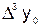












 ,
, .
. , поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей.
, поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей. ,
, – некоторая точка интервала, содержащего узлы интерполяции.
– некоторая точка интервала, содержащего узлы интерполяции. . В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона
. В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона ,
, .
. ,
, и
и 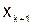 , т.е.
, т.е.  . В этом случае для интерполирования применяется интерполяционная формула Гаусса
. В этом случае для интерполирования применяется интерполяционная формула Гаусса

 ,
, ;
;  – целая часть числа
– целая часть числа  .
. ,
,

 ,
, приближённо можно вычислить следующим образом:
приближённо можно вычислить следующим образом: ,
, Если требуется найти производную в точке
Если требуется найти производную в точке  , лежащей в середине или в конце таблицы, то формулу для её вычисления получаем, исходя из формулы Гаусса или второй интерполяционной формулы Ньютона.
, лежащей в середине или в конце таблицы, то формулу для её вычисления получаем, исходя из формулы Гаусса или второй интерполяционной формулы Ньютона. , соответствующего значения
, соответствующего значения  . Если
. Если  – монотонная непрерывная функция на интервале
– монотонная непрерывная функция на интервале  , причем
, причем  , то функция
, то функция 






 .
. .
. :
: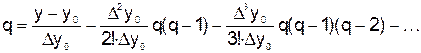 .
. .
.
 . В случае получения расходящегося процесса необходимо уменьшить h. Продолжая процесс итерации, получаем
. В случае получения расходящегося процесса необходимо уменьшить h. Продолжая процесс итерации, получаем
 .
.
 .
. методом обратной интерполяции нужно рассмотреть функцию
методом обратной интерполяции нужно рассмотреть функцию  и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.
и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.


