На минимум. 78.Одномерная безусловная оптимизация методом случайного поиска8 Да Z1< Z2
Нет 9 10
a = xc b = xc Рисунок 3.3. Схема алгоритма программы по методу дихотомии
78.Одномерная безусловная оптимизация методом случайного поиска Методы случайного поиска основаны на формировании на отрезке поиска случайным образом расчетных точек, вычислении в этих точках значений функции и выборе из них экстремального. Точность определяется числом точек поиска n. Повторение испытаний описывается формулой Бернулли (биноминальным распределением)
где k – число благоприятных случаев; n – общее число испытаний; p – вероятность благоприятного исхода при одном испытании; q – вероятность, противоположная p (q=1-p). Вероятность, что событие наступит n раз
что не наступит ни разу
наступит хотя бы один раз
Если абсолютную точность поиска решения на участке (b - a) обозначить через ε, то вероятность решения при одном испытании p = ε/(b - a). При этом вероятности Р1 получения решения в зависимости от числа испытаний n при различных p приведены в таблице 3.1.
Таблица 3.1 – Оценка точности поиска
Например, если p = ε /(b - a)=0.01, то вероятность получения решения с точностью ε при числе испытаний n = 100 равна 0.634; при n =200 – 0.866; при n = 500 – 0.993; при n = 1000 – 0.99996, т.е. требуется 10 (b - a) /ε испытаний для надежного решения (Р1> 0.9999) с заданной точностью ε. Аналогичная зависимость, как видно из таблицы, имеет место и при других точностях решения. Имеется большое множество методов оптимизации на основе случайного поиска и их разновидностей. Ниже приведена иллюстрация простейшего метода поиска, состоящая в последовательном формировании на отрезке от a до b случайным образом расчетной точки xт, расчете в ней целевой функции f(xт), сравнении значения функции f(xт) и ранее найденного "лучшего" значения функции f(xп), присвоении xп =xт и f(xп) =f(xт), если текущая точка "лучше". Формирование случайной точки производится по выражению xт = a + r (b-a), где r – случайное число, равномерно распределенное в интервале от 0 до 1.0.
f(x)
f(xт)
f(xп)
a xп xт b x Рисунок 3.10 – Графическая интепретация метода случайного поиска (на минимум)
Более эффективным является метод случайного поиска с пересчетом, алгоритм которого приведен на рисунке 3.11. Принимаемые значения показателей aш, bш, h и L должны находится в определенном соотношении, например начальные значения могут быть приняты bш = 2; h= bш /5; aш = 0.25; L=10. Формирование случайной расчетной точки xт (блок 9) производится относительно текущего приближения xп на основе использования случайных чисел r, равномерно распределенных в интервале от 0 до 1.0. Произведение sh определяет отрезок, в пределах которого формируется случайная точка. 79.Одномерная безусловная оптимизация методом квадратичной интерполяции-экстраполяции Метод квадратичной интерполяции-экстраполяции является одним из методов аппроксимации кривыми и базируется на приближении целевой функции квадратичной параболой по трем точкам – текущее приближение x1= xп и точки, лежащие от нее слева x0 и справа x2 на удалении h и нахождении экстремума аналитически. Процесс проводится до тех пор, пока предыдущее и последующее приближения различаются более, чем на заданную точность поиска. Алгоритм метода следующий (рисунок 3.8, 3.9): 1. находим x0 = xп - h; y0 = f(x0); x1 = xп; y1 = f(x1); x2 = xп + h; y2 = f(x2); 2. находим параметры параболы, проходящей через три выбранных точки a = (yo- 2y1 + y2) / (2h2); b = (-yo (2x1 + h) + 4y1 x1 - y2 (2x1 - h)) / (2h2); Тогда очередное приближение x на основе аналитической оптимизации аппроксимирующей функции равно xп = - b/(2a); 3. проверяем условие: abs(xп - x1) < e. Если выполняется, то оптимум найден. Иначе переходим к 1-му пункту алгоритма.
На минимум: f(x)
f(x)=ax2+bx+c
f(xп+h) f(xп-h) f(xп)
xп-h xп xп+h x Рисунок 3.8 – Графическая интепретация метода на основе квадратичной аппроксимации
1 Пуск
Ввод xп, h, e xп – текущее значение приближения к решению; h – параметр интервала
9 аппроксимации; e – точность поиска 4 7
b =...
xi = xп +(i-1) h xп = -b/(2a)
6 9 Нет abs(x1- xп)<e 4 yi= f(xi) Да
Zп= f(xп)
11 Рисунок 3.9 – Алгоритм на основе Вывод xп, Zп квадратичной аппроксимации
Останов
80.Модель транспортной сети Транспортная сеть района (региона) представляет собой систему путей сообщения, предназначенную для передвижения транспортных средств. Модель транспортной сети – это описание местонахождения ее вершин (пунктов), а также длин и других параметров (характеристик) соединяющих вершины звеньев. Может быть задана в графическом или табличном виде. Звеном транспортной сети является ее часть, соединяющая две смежные вершины. Длина звеньев может быть выражена в единицах длины, приведенных единицах длины, единицах времени и стоимостном выражении (в дальнейшем длина). В качестве других параметров звеньев может быть задана техническая категория пути сообщения и др. Вершины (пункты) транспортной сети соответствуют местонахождению ресурсообразующих и ресурсопоглащающих точек, терминалов, пересечений путей. Длина звеньев транспортной сети определяется по справочным таблицам, атласам дорог, с помощью курвиметра по масштабным картам и планам, а также непосредственным замером на местности, например по показаниям одометра (счетчика пройденного пути) автомобиля. 81.Многомерная безусловная оптимизация. Схемы методов Розенброка и Пауэлла Метод вращающихся координат (метод Розенброка) имеет следующий алгоритм (рисунок 3.13): 1) принимается начальное (текущее) приближение к решению – точка Xп1 и начальный (текущий) шаг поиска; 2) находится одним из известных методов при текущем значении шага следующее приближение – точка Xп2; 3) по линии Xп1 - Xп2 принимается новое направление поиска (производят поворот осей); 4) модифицируется шаг поиска и вдоль новых осей Z1 и Z2 находится следующее текущее приближение; 5) если результат с заданной точностью получен, то решение закончено или иначе по последнему и предпоследнему приближениям находится новое направление поиска и делается переход на пункт 4.
Метод Пауэлла основан на определении направлений поиска путем проведения касательных к изолиниям (изоповерхностям), параллельных друг другу. Линия, соединяющая точки касания определяет текущее направление поиска Z1. Графическое представление метода приведено на рисунке 3.14.
Рисунок 3.14 – Графическая интерпретация метода Пауэлла 82.Оценка оптимальности решения задачи линейного программирования симплекс-методом Основные шаги решения задачи (после представления исходной системы в стандартном виде): 21) формируется первоначальное базисное решение; 22) выражается Z через небазисные переменные; 23) проверяется базисное решение на оптимальность. Если оптимально, то на п.10; 24) проверяется задача на наличие решения. Если решения нет, то выход; 25) выбирается из небазисных переменных та, которая способна при введении ее в базис в большей степени улучшить значение целевой функции, и вводится в базис; 26) определяется базисная переменная, которая выводится из базиса; 27) алгебраически выражается вводимая в базис переменная через переменную, выводимую из базиса и другие небазисные переменные; 28) алгебраически выражаются другие базисные переменные через небазисные; 29) переход на п. 2; 30) определяются значения базисных переменных. Они являются решением задачи. Итерационный процесс (шаги 2–9) повторяются до тех пор, пока не произойдет выход на шаге 3 или 4. Алгоритм реализации отдельных шагов при решении задачи на максимум и ограничениях типа £ следующий: Шаг 1 состоит в назначении базисных переменных по числу ограничений в задаче. Базисные переменные xu выражаются через небазисные xp из равенств, в которые они входят через значимые коэффициенты. При этом небазисные переменные принимаются нулевыми. На первом шаге в качестве базисных принимаются дополнительные переменные, а в качестве небазисных – основные, т.е. xm+1 = b1; xm+2 = b2; ... xM = bn; x1 = 0; x2 = 0; ... xm = 0. Шаг 2 – алгебраически выражается целевая функция Z через небазисные переменные
Шаг 3 – проверяется все ли сp≤0. Если да, то решение оптимально. Шаг 4 – оценка наличия решения. Если при хp, имеющем сp >0, во всех уравнениях apj<0 (j =1, 2,..., n), то решение отсутствует (выход из программы с соответствующим сообщением). Шаг 5 – определяется та небазисная переменная, которую наиболее целесообразно ввести в базис, по максимуму положительного коэффициента в текущем выражении для целевой функции Шаг 6 – определяется одна из базисных переменных для вывода ее из базиса. Для этого во всех j-х равенствах для хs вычисляется отношение свободного члена bj к соответствующему коэффициенту asj (asj >0), т.е. bj/asj. Минимальное из отношений указывает на j-е равенство и соответственно на выводимую переменную из базиса. Шаг 10 – формируется окончательное решение в виде численных значений искомых переменных, которые входят в базис. Вычисляются из последних выражений для них при значениях небазисных переменных, равных нулю. С практической точки зрения определение численных значений базисных переменных, которые являются дополнительными, не требуется. Основные переменные, которые не входят в базис, равны нулю. 83.Одномерная безусловная оптимизация по методу поразрядного приближения Графическая интепретация и алгоритм поиска экстремума функции на основе поразрядного приближения приведены на рисунках 3.6, 3.7. f(x)
f(xп+h) f(xп) На минимум
xп xп+h x Рисунок 3.6 – Графическая интепретация метода поразрядного приближения
1 Пуск
xп, h, a,e xп и h – текущие значения соответственно приближения к решению и шага поиска; a – коэффициент изменения шага поиска; e – точность поиска решения
Z = f(xп)
Zп = Z
xп = xп + h
Z= f(xп)
|

 , k = 0, 1, 2,..., n,
, k = 0, 1, 2,..., n, ;
; ;
; .
. a =...
a =...
 и
и 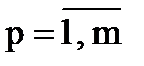 . Тогда первое базисное решение
. Тогда первое базисное решение .
.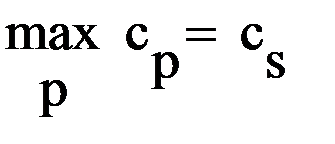 , где s– номер переменной, вводимой в базис.
, где s– номер переменной, вводимой в базис.


