no1. Определение комплексных чисел
Определение 1. Комплексными числами называются всевозможные упорядоченные пары 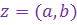 вещественных чисел вещественных чисел 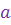 и и 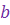 , при этом для этих пар понятия равенства, суммы, произведения и отождествления некоторых пар с вещественными числами вводятся по следующим правилам (аксиомам):
I. , при этом для этих пар понятия равенства, суммы, произведения и отождествления некоторых пар с вещественными числами вводятся по следующим правилам (аксиомам):
I.  (равенство к.ч.)
II. (равенство к.ч.)
II.  (сумма к.ч)
III. (сумма к.ч)
III. 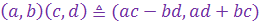 (произведение к.ч.)
IV. (произведение к.ч.)
IV. 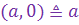 (отождествление некоторых к.ч с в.ч.)
Множество всех комплексных чисел обозначается буквой (отождествление некоторых к.ч с в.ч.)
Множество всех комплексных чисел обозначается буквой 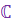 .
Свойства операций сложения и умножения к.ч.
Легко проверить, что операции сложения
коммутативна: .
Свойства операций сложения и умножения к.ч.
Легко проверить, что операции сложения
коммутативна: 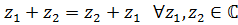 и
ассоциативна:
и
ассоциативна: 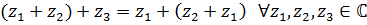 Комплексное и, в соответствии с IV, одновременно вещественное число
Комплексное и, в соответствии с IV, одновременно вещественное число 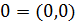 очевидно обладает тем свойством, что очевидно обладает тем свойством, что
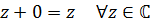 Комплексное число
Комплексное число
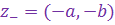 называется противоположным к.ч.
называется противоположным к.ч. 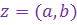 , при этом очевидно , при этом очевидно
 Нетрудно убедиться, что операция умножения комплексных чисел.
коммутативна:
Нетрудно убедиться, что операция умножения комплексных чисел.
коммутативна:  ассоциативна:
ассоциативна: 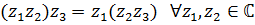 дистрибутивна по отношению к сложению:
дистрибутивна по отношению к сложению:
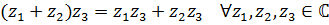 Отметим, что для любого к.ч.
Отметим, что для любого к.ч. 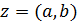 в соответствии с определением операции умножения в соответствии с определением операции умножения
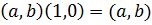 и, следовательно пара
и, следовательно пара 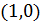 играет роль единицы при умножении к.ч., что согласуется с тем, что комплексное число играет роль единицы при умножении к.ч., что согласуется с тем, что комплексное число 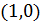 отождествляется с вещественным числом 1.
Вообще отметим, что в соответствии с аксиомами III и IV отождествляется с вещественным числом 1.
Вообще отметим, что в соответствии с аксиомами III и IV
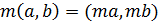 Действительно,
Действительно,
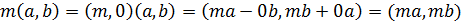 Вычитание и деление к.ч.
Разность к.ч. вводится на основе операции сложения и понятия противоположного к.ч. по следующему правилу:
Вычитание и деление к.ч.
Разность к.ч. вводится на основе операции сложения и понятия противоположного к.ч. по следующему правилу:
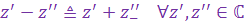 Пусть к.ч.
Пусть к.ч. 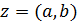 отлично от нуля, т.е. отлично от нуля хотя бы одно из вещественных чисел отлично от нуля, т.е. отлично от нуля хотя бы одно из вещественных чисел  и и  . Тогда к.ч. . Тогда к.ч.
 называется обратным к к.ч.
называется обратным к к.ч. 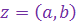 .
Очевидно, .
Очевидно,
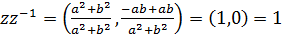 .
Операция деления к.ч. вводится на основе операции умножения и введенного выше понятия обратного к.ч. А именно, частным от деления к.ч. .
Операция деления к.ч. вводится на основе операции умножения и введенного выше понятия обратного к.ч. А именно, частным от деления к.ч.  на к.ч. на к.ч. 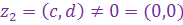 называется к.ч. называется к.ч.
 Замечание1. Нетрудно показать, что при умножении числителя и знаменателя дроби
Замечание1. Нетрудно показать, что при умножении числителя и знаменателя дроби  на одно и то же к.ч. на одно и то же к.ч. 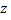 она не изменится, т.е она не изменится, т.е
 Комплексное число
Комплексное число
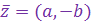 называется комплексно сопряженным к (для) к.ч.
называется комплексно сопряженным к (для) к.ч.
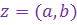 .
Ясно, что к.ч. .
Ясно, что к.ч.
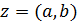 ,
в свою очередь, является комплексно сопряженным к к.ч. ,
в свою очередь, является комплексно сопряженным к к.ч.
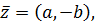 т.е. комплексно сопряженное к комплексно сопряженному для к.ч.
т.е. комплексно сопряженное к комплексно сопряженному для к.ч. 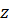 есть само к.ч. есть само к.ч. 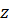 .
Для любой пары комплексно сопряженных чисел .
Для любой пары комплексно сопряженных чисел
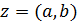 и и 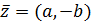 ,
очевидно, ,
очевидно,
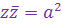 + + 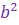 .
Действительно, .
Действительно,
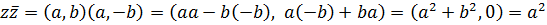 + + 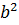 Таким образом произведение
Таким образом произведение 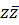 к.ч. на ему комплексно сопряженное является вещественным числом.
no2. Алгебраическая форма к.ч.
К.ч. к.ч. на ему комплексно сопряженное является вещественным числом.
no2. Алгебраическая форма к.ч.
К.ч. 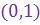 называется мнимой единицей и обозначается буквой называется мнимой единицей и обозначается буквой 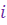 .
Таким образом, .
Таким образом, 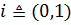 .
По определению умножения к.ч. имеем .
По определению умножения к.ч. имеем
 Следовательно,
Следовательно,
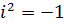 Для любого комплексного числа
Для любого комплексного числа 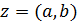 , очевидно, что , очевидно, что
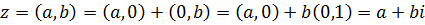 (здесь нужно учесть, что
(здесь нужно учесть, что  а по аксиоме IV а по аксиоме IV  ).
Запись к.ч. ).
Запись к.ч. 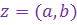 в виде в виде
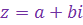 называется алгебраической формой записи этого к.ч., при этом вещественное число
называется алгебраической формой записи этого к.ч., при этом вещественное число  называют вещественной частью к.ч. называют вещественной частью к.ч.  и обозначают и обозначают 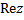 , а в.ч. , а в.ч.  называют его мнимой частью и обозначают называют его мнимой частью и обозначают 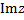 ( (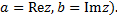 Ясно, что число, комплексно сопряженное к к.ч.
Ясно, что число, комплексно сопряженное к к.ч. 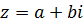 в алгебраической форме записи имеет вид в алгебраической форме записи имеет вид
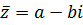 ,
а операции сложения, умножения, вычитания и деления при использовании алгебраической форме записи к.ч. производятся по формулам: ,
а операции сложения, умножения, вычитания и деления при использовании алгебраической форме записи к.ч. производятся по формулам:
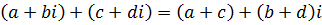 , ,
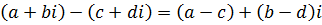 , ,
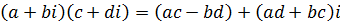 , ,
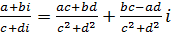 .
Необходимости запоминать две последние формулы нет. Для того, чтобы получить третью из этих формул достаточно перемножить выражения, стоящие в ней слева по обычным правилам действия с алгебраическими выражениями, затем привести подобные члены и учесть, что .
Необходимости запоминать две последние формулы нет. Для того, чтобы получить третью из этих формул достаточно перемножить выражения, стоящие в ней слева по обычным правилам действия с алгебраическими выражениями, затем привести подобные члены и учесть, что 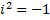 . В свою очередь, что бы получить последнюю из них, с учетом замечания 1, достаточно умножить числитель и знаменатель дроби на к.ч. сопряженное знаменателю и затем произвести умножение к.ч. в числителе и знаменателе полученной дроби.
Примеры
1. . В свою очередь, что бы получить последнюю из них, с учетом замечания 1, достаточно умножить числитель и знаменатель дроби на к.ч. сопряженное знаменателю и затем произвести умножение к.ч. в числителе и знаменателе полученной дроби.
Примеры
1. 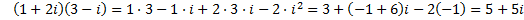 2.
2.  no3 .Тригонометрическая форма к.ч.
Пусть на плоскости введена декартова прямоугольная система координат
no3 .Тригонометрическая форма к.ч.
Пусть на плоскости введена декартова прямоугольная система координат  . Тогда каждому к.ч. . Тогда каждому к.ч. 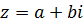 можно сопоставить точку на этой плоскости с координатами можно сопоставить точку на этой плоскости с координатами  и и  по осям по осям  и и 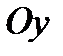 , соответственно. При этом каждому к.ч. соответствует точка на этой плоскости, а каждой точке на ней - определенное к.ч.
Таким образом, к.ч. , соответственно. При этом каждому к.ч. соответствует точка на этой плоскости, а каждой точке на ней - определенное к.ч.
Таким образом, к.ч. 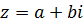 соответствует точка соответствует точка 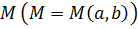 . Длину ее радиус-вектора . Длину ее радиус-вектора 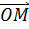 обозначим обозначим 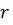 , ,
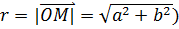 ,
Предполагая, что ,
Предполагая, что  (т.е., что (т.е., что 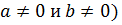 угол между радиус-вектором угол между радиус-вектором 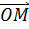 и положительным направлением оси и положительным направлением оси  , отсчитываемым от нее против часовой стрелки, обозначим через , отсчитываемым от нее против часовой стрелки, обозначим через 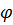 . Тогда для координат точки . Тогда для координат точки 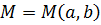 будем иметь формулы будем иметь формулы
 и, следовательно, к.ч.
и, следовательно, к.ч. 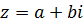 можно записать в виде можно записать в виде
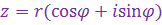 Такая форма записи к.ч.
Такая форма записи к.ч. 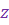 называется тригонометрической формой записи этого к.ч., при этом (заведомо неотрицательное) вещественное число называется тригонометрической формой записи этого к.ч., при этом (заведомо неотрицательное) вещественное число  называют модулем к.ч. называют модулем к.ч. 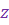 и обозначают и обозначают 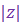 , а число , а число 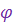 называют аргументом к.ч. называют аргументом к.ч. 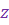 и обозначают и обозначают  .
Модуль к.ч. .
Модуль к.ч. 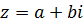 определяется однозначно, определяется однозначно,
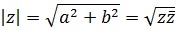 а аргумент
а аргумент 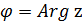 , - с точностью до слагаемого, кратного , - с точностью до слагаемого, кратного  , исходя из уравнений , исходя из уравнений
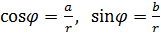 .
Подчеркнем здесь еще раз, что аргумент не определен для к.ч. .
Подчеркнем здесь еще раз, что аргумент не определен для к.ч.  .
Примеры
3. .
Примеры
3. 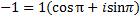 4.
4. 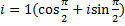 5.
5.  6.
6. 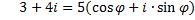 , где , где 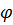 -угол первой четверти, косинус которого равен -угол первой четверти, косинус которого равен  .
Умножение комплексных чисел в тригонометрической форме записи.
Пусть .
Умножение комплексных чисел в тригонометрической форме записи.
Пусть
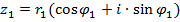 и
и
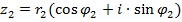 Тогда
Тогда

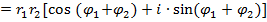
|
(1)
|
Таким образом,
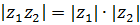 , ,
| (2)
|
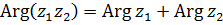 , ,
| (3)
|
т.е. при умножении к.ч. их модули перемножаются, а аргументы складываются (модуль произведения равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей).
Исходя из формулы (1) индукцией по  легко устанавливается, что для любых к.ч. легко устанавливается, что для любых к.ч.
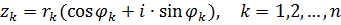
имеет место формула
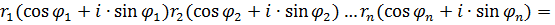
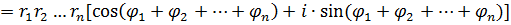
|
(4)
|
а следовательно имеют место и формулы
 , ,
| (5)
| и
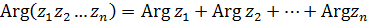 , ,
| (6)
|
no4 .Извлечение корня 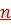 -ой степени из комплексного числа. -ой степени из комплексного числа. Положим в (4)
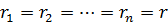 , ,
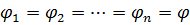 . .
получим формулу 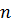 -ой степени к.ч. -ой степени к.ч.
.
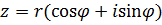
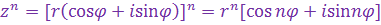 . .
| (7)
|
При 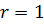 отсюда следует формула Муавра: отсюда следует формула Муавра:
 . .
| (8)
| Предыдущую формулу (7) также иногда называют формулой Муавра.
Нетрудно убедиться, что формула Муавра (8) справедлива не только для целых положительных 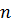 , но и при неположительных целых , но и при неположительных целых 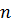 . .
Определение 1. Пусть 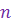 - натуральное число. Корнем - натуральное число. Корнем 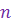 -ой степени из к.ч. -ой степени из к.ч. 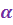 называется к.ч. называется к.ч. 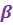 такое, что такое, что 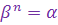 . . Корень 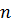 -ой степени из к.ч. -ой степени из к.ч. 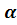 обозначается обозначается 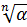 . .
Найдем все корни 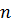 -ой степени из к.ч. -ой степени из к.ч. 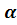 . Если . Если 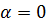 , то единственным значением , то единственным значением 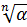 является число 0. Поэтому пусть является число 0. Поэтому пусть 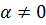 . Запишем . Запишем  в тригонометрической форме в тригонометрической форме
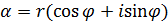
и будем искать 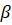 также в тригонометрической форме также в тригонометрической форме
 . .
С учетом формулы (7) запишем равенство 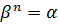 в виде в виде
 . .
Но данное равенство равносильно следующим равенствам:
 , ,
и
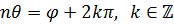 , ,
(здесь учитывается многозначность аргумента к.ч.).
Следовательно,
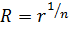 , ,
а
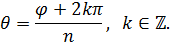
Таким образом, всевозможные корни 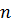 -ой степени и -ой степени и |