Порядок выполнения и защиты типового расчета
Еще один закон, предложенный Торндайком, касался врожденного комплекса движений. Если действия, совершенные в определенной ситуации, приводят к успешным результатам, то их можно назвать удовлетворяющими, в противном случае они будут нарушающими. Понятие успешного результата Торндайк дает на уровне нейронов. При успешном действии система нейронов, приведенная в готовность, на самом деле функционирует, а не бездействует.
Его вклад в науку оценен по достоинству многими учеными и исследователями, к примеру, основателем бихевиоризма Джоном Уотсоном и русским ученым И. П. Павловым.
Объективность и точность сделали труды Торндайка классическими. Своими работами Торндайк показал, что психология как наука выходит далеко за рамки простой механики и биологии. В ее основании лежат совсем другие начала, а сфера исследования распространяется помимо самого организма и на область его взаимодействия с внешней средой. Хотя биопсихические схемы Торндайка были довольно ограниченными, он проложил новый путь в развитии науки психологии, подготовив почву для возникновения бихевиоризма. Разрабатывал впоследствии проблемы поведенческой психологии. Написал учебник по психологии образования. Ему принадлежит серия работ по психологии обучения арифметике, алгебре, языку, чтению. Для количественного определения уровня психического развития он разработал систему ментиметрических приемов (тестов), Внес существенный вклад в область измерения интеллекта и способов отбора персонала.
Еще один закон, предложенный Торндайком, касался врожденного комплекса движений. Если действия, совершенные в определенной ситуации, приводят к успешным результатам, то их можно назвать удовлетворяющими, в противном случае они будут нарушающими. Понятие успешного результата Торндайк дает на уровне нейронов. При успешном действии система нейронов, приведенная в готовность, на самом деле функционирует, а не бездействует.
Его вклад в науку оценен по достоинству многими учеными и исследователями, к примеру, основателем бихевиоризма Джоном Уотсоном и русским ученым И. П. Павловым.
Объективность и точность сделали труды Торндайка классическими. Своими работами Торндайк показал, что психология как наука выходит далеко за рамки простой механики и биологии. В ее основании лежат совсем другие начала, а сфера исследования распространяется помимо самого организма и на область его взаимодействия с внешней средой. Хотя биопсихические схемы Торндайка были довольно ограниченными, он проложил новый путь в развитии науки психологии, подготовив почву для возникновения бихевиоризма. МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ МАРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ НЕОПРЕДЕЛЁННЫЙ И ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛЫ Типовой расчет для студентов Специальностей 060800, 061000, 061100, 061500 Йошкар-Ола УДК 51.517.3 (07)
Неопределённый и определённый интегралы: Типовой расчет / Сост. Ю.А.Фомина, Л.Н.Шарафутдинова. - Йошкар-Ола: МарГТУ, 2004.- 84с.
Приведены 40 вариантов заданий, составленных в соответствии с учебным планом по разделу «Неопределённые и определённые интегралы». Для студентов 1 курса факультета управления и права дневной формы обучения
Печатается по решению редакционно-издательского совета МарГТУ
Рецензент: заведующий кафедрой математического анализа и теории функции МарГУ, кандидат физ.-мат. наук, доцент В.П. Микка
© МарГТУ, 2004
Порядок выполнения и защиты типового расчета
1. Выполнение и защита типового расчета проводится по графику самостоятельной работы студентов. 2. Все задачи должны быть решены письменно и подробно. Нумерация задач должна совпадать с их номером в типовом расчете. 3. Во время защиты типового расчета студент должен уметь отвечать на теоретические вопросы, пояснять решения задач, решать задачи аналогичного типа. 4. Типовой расчет следует выполнять в отдельной тетради. Первая страница оформляется по следующему образцу:
Вариант 1.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислите определённый интеграл:
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
10. Вычислите определённый интеграл, используя указанную замену переменной:
11. Вычислите несобственные интегралы либо докажите их расходимость:
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 2.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислите определённый интеграл:
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
10. Вычислите определённый интеграл, используя указанную замену переменной:
11. Вычислите несобственные интегралы либо докажите их расходимость:
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 3.
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 4.
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 5.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислите определённый интеграл:
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
10. Вычислите определённый интеграл, используя указанную замену переменной:
11. Вычислите несобственные интегралы либо докажите их расходимость:
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 6.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислите определённый интеграл:
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
10. Вычислите определённый интеграл, используя указанную замену переменной:
11. Вычислите несобственные интегралы либо докажите их расходимость:
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 7.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислите определённый интеграл:
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
10. Вычислите определённый интеграл, используя указанную замену переменной:
11. Вычислите несобственные интегралы либо докажите их расходимость:
12. Вычислите площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 8.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислите определённый интеграл:
9. Вычислите определённый интеграл, используя формулу интегрирования по частям:
10. Вычислитe определённый интеграл, используя указанную замену переменной:
11. Вычислитe несобственные интегралы либо докажите их расходимость:
12. Вычислитe площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 9.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислитe определённый интеграл:
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
10. Вычислитe определённый интеграл, используя указанную замену переменной:
11. Вычислитe несобственные интегралы либо докажите их расходимость:
12. Вычислитe площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 10.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислитe определённый интеграл:
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
10. Вычислитe определённый интеграл, используя указанную замену переменной:
11. Вычислитe несобственные интегралы либо докажите их расходимость:
12. Вычислитe площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 11.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислитe определённый интеграл:
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
10. Вычислитe определённый интеграл, используя указанную замену переменной:
11. Вычислитe несобственные интегралы либо докажите их расходимость:
12. Вычислитe площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 12.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислитe определённый интеграл:
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
10. Вычислитe определённый интеграл, используя указанную замену переменной:
11. Вычислитe несобственные интегралы либо докажите их расходимость:
12. Вычислитe площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 13.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
4. Найдите неопределённые интегралы от тригонометрических функций:
5. Найдите неопределённые интегралы:
6. Найдите неопределённые интегралы от дробно-рациональных функций:
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
8. Вычислитe определённый интеграл:
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
10. Вычислитe определённый интеграл, используя указанную замену переменной:
11. Вычислитe несобственные интегралы либо докажите их расходимость:
12. Вычислитe площадь фигуры, ограниченной линиями: а)
б) прямыми
Вариант 14.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
|

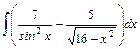 ;
;
 .
.
 ;
;
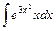 .
.
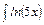 dx;
dx;
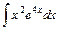 .
.
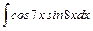 ;
;
 .
.
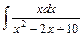 ;
;
 .
.
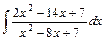 ;
;
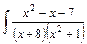 dx.
dx.
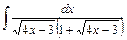 ;
;
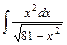 .
.
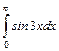 ;
;
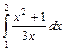 .
.
 .
. ,
, 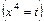 .
. ;
;
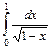 .
.
 ,
, 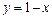 ;
;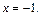
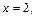
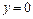 и графиком функции
и графиком функции .
.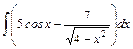 ;
;
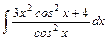 .
.
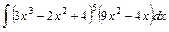 ;
;
 .
.
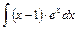 ;
;
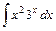 .
.
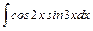 ;
;
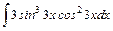 .
.
 ;
;
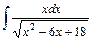 .
.
 ;
;
 dx.
dx.
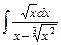 ;
;
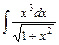 .
.
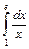 ;
;
 .
.
 .
.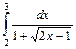 ,
,  .
. ;
;
 .
.
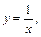
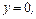
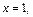
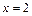 ,
, .
.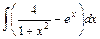 ;
;
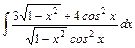 .
.
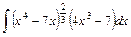 ;
;
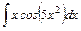 .
.
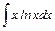 ;
;
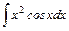 .
.
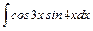 ;
;
 .
.
 ;
;
 .
.
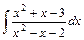 ;
;
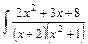 dx.
dx.
 ;
;
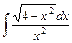 .
.
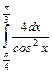 ;
;
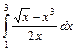 .
.
 .
.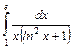 ,
, 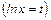 .
.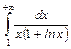 ;
;
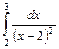 .
.
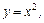
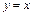 ,
,
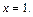
 ;
;
 .
.
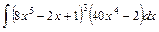 ;
;
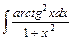 .
.
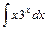 ;
;
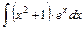 .
.
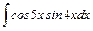 ;
;
 .
.
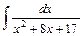 ;
;
 .
.
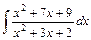 ;
;
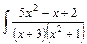 dx.
dx.
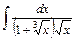 ;
;
 .
.
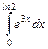 ;
;
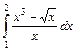 .
.
 .
.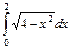 ,
,  .
. ;
;
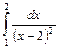 .
.
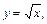

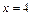 ,
,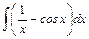 ;
;
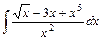 .
.
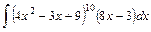 ;
;
 .
.
 ;
;
 .
.
 ;
;
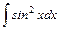 .
.
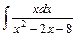 ;
;
 .
.
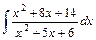 ;
;
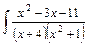 dx.
dx.
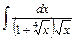 ;
;
 .
.
 ;
;
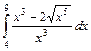 .
.
 .
. ,
,  .
. ;
;
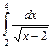 .
.
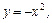
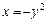 ,
, ;
;
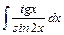 .
.
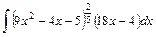 ;
;
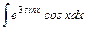 .
.
 ;
;
 .
.
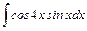 ;
;
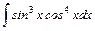 .
.
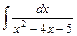 ;
;
 .
.
 ;
;
 dx.
dx.
 ;
;
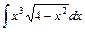 .
.
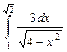 ;
;
 .
.
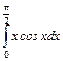 .
.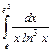 ,
,  ;
;
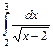 .
.
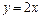 ,
,
 .
. ;
;
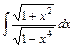 .
.
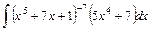 ;
;
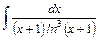 .
.
 ;
;
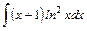 .
.
 ;
;
 .
.
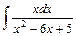 ;
;
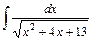 .
.
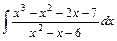 ;
;
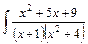 dx.
dx.
 ;
;
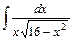 .
.
 ;
;
 .
.
 .
. ,
, 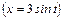
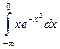 ;
;
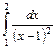 .
.
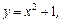
 ,
, .
.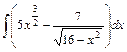 ;
;
 .
.
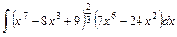 ;
;
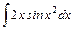 .
.
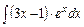 ;
;
 .
.
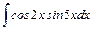 ;
;
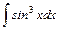 .
.
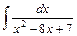 ;
;
 .
.
 ;
;
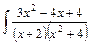 dx.
dx.
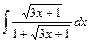 ;
;
 .
.
 ;
;
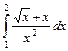 .
.
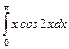 .
. ,
, 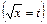 .
.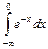 ;
;
 .
.
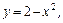
 ,
, ;
;
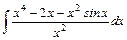 .
.
 ;
;
 .
.
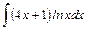 ;
;
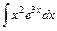 .
.
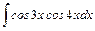 ;
;
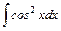 .
.
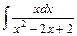 ;
;
 .
.
 ;
;
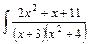 dx.
dx.
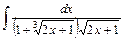 ;
;
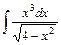 .
.
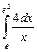 ;
;
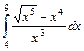 .
.
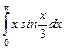 .
.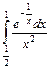 ,
,  .
.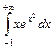 ;
;
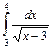 .
.
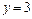 ,
, ;
;
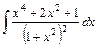 .
.
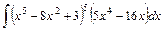 ;
;
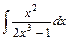 .
.
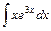 ;
;
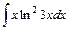 .
.
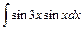 ;
;
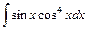 .
.
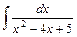 ;
;
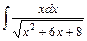 .
.
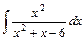 ;
;
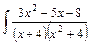 dx.
dx.
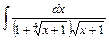 ;
;
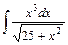 .
.
 ;
;
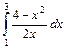 .
.
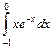 .
.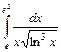 ,
,  .
.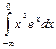 ;
;
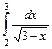 .
.
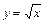 ,
,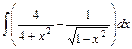 ;
;
 .
.
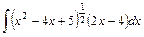 ;
;
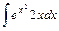 .
.
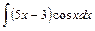 ;
;
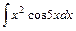 .
.
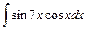 ;
;
 .
.
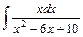 ;
;
 .
.
 ;
;
 dx.
dx.
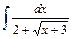 ;
;
 .
.
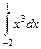 ;
;
 .
.
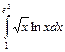 .
.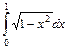 ,
,  .
. ;
;
 .
.

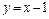 ,
, ;
;
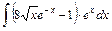 .
.
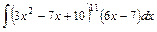 ;
;
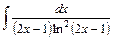 .
.
 ;
;
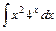 .
.
 ;
;
 .
.
 ;
;
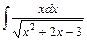 .
.
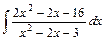 ;
;
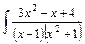 dx.
dx.
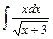 ;
;
 .
.
 ;
;
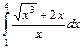 .
.
 .
. ,
,  ;
;
 .
.
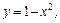
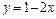 ,
, ;
;
 .
.
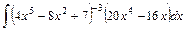 ;
;
 .
.
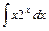 ;
;
 .
.
 ;
;
 .
.
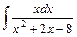 ;
;
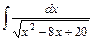 .
.
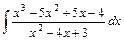 ;
;
 dx.
dx.
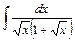 ;
;
 .
.
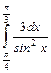 ;
;
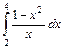 .
.
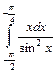 .
.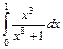 ,
,  .
.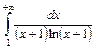 ;
;
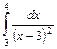 .
.
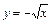 ,
, ;
;
 .
.



