ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
1. Найти координаты вектора x в базисе {a,b,c}:
Указание: при решении системы применить правило Крамера.
1.1. x ={ -2, 4, 7 }, a ={ 0, 1, 2 }, b ={ 1, 0, 1 }, c ={ -1, 2, 4 }.
1.2. x ={ 6, 12, -1 }, a ={ 1, 3, 0 }, b ={ 2, -1, 1 }, c ={ 0, -1, 2 }.
1.3. x ={ 1, -4, 4 }, a ={ 2, 1, -1 }, b ={ 0, 3, 2 }, c ={ 1, -1, 1 }.
1.4. x ={ -9, 5, 5 }, a ={ 4, 1, 1 }, b ={ 2, 0, -3 }, c ={ -1, 2, 1 }.
1.5. x ={ -5, -5, 5 }, a ={ -2, 0, 1 }, b ={ 1, 3, -1 }, c ={ 0, 4, 1 }.
1.6. x ={ 13, 2, 7 }, a ={ 5, 1, 0 }, b ={ 2, -1, 3 }, c ={ 1, 0, -1 }.
1.7. x ={-19, -1, 7 }, a ={ 0, 1, 1 }, b ={ -2, 0, 1 }, c ={ 3, 1, 0 }.
1.8. x ={ 3, -3, 4 }, a ={ 1, 0, 2 }, b ={ 0, 1, 1 }, c ={ 2, -1, 4 }.
1.9. x ={ 3, 3, -1 }, a ={ 3, 1, 0 }, b ={ -1, 2, 1 }, c ={ -1, 0, 2 }.
1.10. x ={ -1, 7, -4 }, a ={ -1, 2, 1 }, b ={ 2, 0, 3 }, c ={ 1, 1, -1 }. 1.11. x ={ 6, 5, -14 }, a ={ 1, 1, 4 }, b ={ 0, -3, 2 }, c ={ 2, 1, -1 }.
1.12. x ={ 6, -1, 7 }, a ={ 1, -2, 0 }, b ={ -1, 1, 3 }, c ={ 1, 0, 4 }.
1.13. x ={ 5, 15, 0 }, a ={ 1, 0, 5 }, b ={ -1, 3, 2 }, c ={ 0, -1, 1 }.
1.14. x ={ 2, -1, 11 }, a ={ 1, 1, 0 }, b ={ 0, 1, -2 }, c ={ 1, 0, 3 }.
1.15. x ={ 11, 5, -3 }, a ={ 1, 0, 2 }, b ={ -1, 0, 1 }, c ={ 2, 5, -3 }.
1.16. x ={ 8, 0, 5 }, a ={ 2, 0, 1 }, b ={ 1, 1, 0 }, c ={ 4, 1, 2 }.
1.17. x ={ 3, 1, 8 }, a ={ 0, 1, 3 }, b ={ 1, 2, -1 }, c ={ 2, 0, -1 }.
1.18. x ={ 8, 1, 12 }, a ={ 1, 2, -1 }, b ={ 3, 0, 2 }, c ={ -1, 1, 1 }.
1.19. x ={ -9, -8, -3 }, a ={ 1, 4, 1 }, b ={ -3, 2, 0 }, c ={ 1, -1, 2 }.
1.20. x ={ -5, 9, -13 }, a ={ 0, 1, -2 }, b ={ 3, -1, 1 }, c ={ 4, 1, 0 }.
1.21. x ={ 2, 7, 5 }, a ={ 1, 0, 1 }, b ={ 1, -2, 0 }, c ={ 0, 3, 1 }.
1.22. x ={ 15, -20, -1 }, a ={ 0, 2, 1 }, b ={ 0, 1, -1 }, c ={ 5, -3, 2 }.
1.23 х= { 10, 1, 11 }, a = { 3, 1, -1}, b ={ 1, -1, 4}, c= { 2, 1, 5}
1.24 x= { 0, 6, -1}, a ={ -1, 2, 1}, b ={ 2, 1, -1}, c= { 1, 2, 2}
2. Даны координаты вершин тетраэдра А1 А2 А3 А4. Найти: 1) длину ребра А1 А2; 2) угол между ребрами А1 А2 и А1 А4; 3) угол между ребром А1 А4 и гранью А1 А2 А3; 4) площадь грани А1 А2 А3; 5) объем тетраэдра; 6) уравнения прямой А1А2; 7) уравнение плоскости А1 А2 А3; 8) уравнения высоты, опущенной из вершины А4 на грань А1 А2 А3; 9) расстояние вершины А4 до грани А1 А2 А3; 10) расстояние вершины А4 до ребра А1 А2.
Указание: все результаты представить точно в виде радикалов, а затем привести их приближенные значения.
А 1 А 2 А 3 А 4 2.1. (1, 3, 6) (2, 2, 1) (-1, 0, 1) (-4, 6, -3) 2.2. (-4, 2, 6) (2, -3, 0) (-10, 5, 8) (-5, 2, -4) 2.3. (7, 2, 4) (7, -1, -2) (3, 3, 1) (-4, 2, 1) 2.4. (2, 1, 4) (-1, 5, -2) (-7, -3, 2) (-6, -3, 6) 2.5. (-1, -5, 2) (-6, 0, -3) (3, 6, -3) (-10, 6, 7) 2.6. (0, -1, -1) (-2, 3, 5) (1, -5, -9) (-1, -6, 3) 2.7. (5, 2, 0) (2, 5, 0) (1, 2, 4) (-1, 1, 1) 2.8. (2, -1, -2) (1, 2, 1) (5, 0, -6) (-10, 9, -7) 2.9. (-2, 0, -4) (-1, 7, 1) (4, -8, - 4) (1, - 4, 6) 2.10. (14, 4, 5) (-5, -3, 2) (-2, -6, -3) (-2, 2, -1) 2.11. (1, 2, 0) (3, 0, -3) (5, 2, 6) (8, 4, -9) 2.12. (2, -1, 2) (1, 2, -1) (3, 2, 1) (-4, 2, 5) 2.13. (1, 1, 2) (-1, 1, 3) (2, -2, 4) (-1, 0, -2) 2.14. (2, 3, 1) (4, 1, -2) (6, 3, 7) (7, 5, -3) 2.15. (1, 1, -1) (2, 3, 1) (3, 2, 1) (5, 9, -8) 2.16. (1, 5, -7) (-3, 6, 3) (-2, 7, 3) (-4, 8, -12) 2.17. (-3, 4, -7) (1, 5, -4) (-5, -2, 0) (2, 5, 4) 2.18. (-1, 2, -3) (4, -1, 0) (2, 1, -2) (3, 4, 5) 2.19. (4, -1, 3) (-2, 1, 0) (0, -5, 1) (3, 2, -6) 2.20. (1, -1, 1) (-2, 0, 3) (2, 1, -1) (2, -2, -4) 2.21. (2, -4, -3) (5, -6, 0) (-1, 3, -3) (-10, -8, 7) 2.22. (1, -1, 2) (2, 1, 2) (1, 1, 4) (6, -3, 8) 2.23. (-1, 2, 4) (-1, -2, -4) (3, 0, -1) (7, -3, 1) 2.24. (0, -3, 1) (-4, 1, 2) (2, -1, 5) (3, 1, -4) 3. Линия задана уравнением 1) построить линию по точкам, начиная от 2) найти уравнение данной линии в декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по уравнению в декартовых координатах определить, какая это линия.
3.1. r =2/(1+cos 3.4. r =10/(2+cos 3.7. r =5/(2-cos 3.10. r =5/(1-2cos 3.13. r =2/(2+5cos 3.16. r =3/(5-2cos 3.19. r =1/(4-cos 3.22. r =2/(5-3cos
4. Решить систему уравнений: 1) методом Гаусса; 2) средствами матричного исчисления (x=A_-1 B); Указание: вычисления проводить с обычными дробями, не используя десятичных приближений.
5. Найти какой-нибудь базис и определить размерность линейного пространства решений системы:
5.1. 3x1 + x2 - 8x3 + 2x4 + x5 = 0 5.2. 7x1 + 2x2 - x3 - 2x4 + 2x5 = 0 2x1 - 2x2 - 3x3 - 7x4 + 2x5 = 0 x1 - 3x2 + x3 - x4 - x5 = 0 x1 + 11x2 - 12x3 + 34x4 - 5x5 = 0 2x1 + 5x2 + 2x3 + x4 + x5 = 0
5.3. x1 + x2 + 10x3 + x4 - x5 = 0 5.4. 6x1 - 9x2 + 21x3 - 3x4 - 12x5 = 0 5x1 - x2 + 8x3 - 2x4 + 2x5 = 0 -4x1 + 6x2 - 14x3 + 2x4 + 8x5 = 0 3x1 - 3x2 - 12x3 - 4x4 + 4x5 = 0 2x1 - 3x2 + 7x3 - x4 - 4x5 = 0
5.5. 2x1 - x2 + 2x3 - x4 + x5 = 0 5.6. 5x1 - 2x2 + 3x3 - 4x4 - x5 = 0 x1 + 10x2 - 3x3 - 2x4 - x5 = 0 x1 + 4x2 - 3x3 + 2x4 - 5x5 = 0 4x1 + 19x2 - 4x3 - 5x4 - x5 = 0 6x1 + 2x2 - 2x4 - 6x5 = 0
5.7. 12x1 - x2 + 7x3 + 11x4 - x5 = 0 5.8. x1 + 2x2 + x3 + 4x4 + x5 = 0 24x1- 2 x2 + 14x3 + 22x4 -2x5 = 0 2x1 - x2 + 3x3 + x4 - 5x5 = 0 x1 + x2 + x3 - x4 + x5 = 0 x1 + 3x2 - x3 - 6x4 - x5 = 0
5.9. 2x1 - x2 + 3x3 - x4 - x5 = 0 5.10. x1 + x2 + x3 + 2x4 + x5 = 0 x1 + 5x2 - x3 + x4 + 2x5 = 0 x1 - 2x2 - 3x3 + x4 - x5 = 0 x1 + 16x2 - 6x3 + 4x4 + 7x5 = 0 2x1 - x2 - 2x3 + 3x4 = 0
5.11. 8x1 + x2 + x3 - x4 + 2x5 = 0 5.12. x1 + 3x2 - x3 + 12x4 - x5 = 0 3x1 - 3x2 - 2x3 + x4 - 3x5 = 0 2x1 - 2x2 + x3 - 10x4 + x5 = 0 5x1 + 4x2 + 3x3 - 2x4 + 5x5 = 0 3x1 + x2 + 2x4 = 0
5.13. 7x1 - 14x2 + 3x3 - x4 + x5 = 0 5.14. x1 + 2x2 + 3x3 + x4 - x5 = 0 x1 - 2x2 + x3 - 3x4 + 7x5 = 0 2x1 - 2x2 - 5x3 - 3x4 + x5 = 0 5x1 - 10x2 + x3 + 5x4 - 13x5 = 0 3x1 - 2x2 + 3x3 + 2x4 - x5 = 0
5.15. x1 + x2 + x3 - x4 - x5 = 0 5.16. 2x1 + x2 - 3x3 + x4 - x5 = 0 2x1 + x2 - 2x3 - x4 - 2x5 = 0 3x1 - x2 + 2x3 - x4 + 2x5 = 0 x1 + 2x2 + 5x3 - 2x4 - x5 = 0 x1 - 2x2 + 5x3 - 2x4 + 3x5 = 0
5.17. x1 + 2x2 - 3x3 + 10x4 -x5 = 0 5.18. 2x1 + x2 - x3 + 7x4 + 5x5 = 0 x1 - 2x2 + 3x3 - 10x4 + x5 = 0 x1 - 2x2 + 3x3 - 5x4 - 7x5 = 0 x1 + 6x2 - 9x3 + 30x4 - 3x5 = 0 3x1 - x2 + 2x3 + 2x4 - 2x5 = 0
5.19. 2x1 - 2x2 - 3x3 - 7x4 + 2x5 = 0 5.20. 3x1 + x2 - 8x3 + 2x4 + x5 = 0 x1 + 11x2 - 12x3+ 34x4 - 5x5 = 0 x1 + 11x2 -12x3 - 34x4 - 5x5 = 0 x1 - 5x2 + 2x3 - 16x4 + 3x5 = 0 x1 - 5x2 + 2x3 - 16x4 + 3x5 = 0
5.21. 3x1 + 2x2 - 2x3 - x4 + 4x5 = 0 5.22 x1 + x2 +3x3 - 2x4 +3x5 = 0 7x1 + 5x2 - 3x3 - 2x4 + x5 = 0 2x1 + 2x2 + 4x3 – x4 +3x5 = 0 x1 + x2 + x3 - 7x5 = 0 x1 + x2 + 5x3 – 5x4 + 6x5 = 0
5.23 x1 + 2x2 + 3x3 – 2x4 +x5 = 0 5.24 x1 + x2 + x3 + 2x4 +x5 = 0 x1 + 2x2 + 7x3 – 4x4 +x5 = 0 x1 – 2x2 – 3x3 +x4 – x5 = 0 x1 + 2x2 + 11x3 – 6x4 + x5 = 0 2x1 – x2 – 2x3 + 3x4 = 0
Пример решения: 5x1 + 2x2 - x3 + 3x4 + 4x5 = 0 3x1 + x2 - 2x3 + 3x4 + 5x5 = 0 6x1 + 3x2 - 2x3 + 4x4 + 7x5 = 0
Выпишем матрицу системы, нумеруя столбцы (нумеровать строки необязательно):
5 2 -1 3 4 3 1 -2 3 5 6 3 -2 4 7 (1) (2) (3) (4) (5)
и приведем ее к каноническому виду, применяя элементарные преобразования: умножение строки на число, перестановку строк, сложение строк, те же операции со столбцами. При этом следим за переставляемыми столбцами по их номерам.
1) Расположим в левом верхнем углу элемент, равный 1. (Если такого элемента в матрице нет, то следует поделить любой столбец на любой отличный от 0 его элемент). Для этого поменяем местами строки (1) и (2):
3 1 -2 3 5 5 2 -1 3 4 6 3 -2 4 7 (1) (2) (3) (4) (5)
Теперь поменяем столбцы (1) и (2):
1 3 -2 3 5 [-2], [-3] 2 5 -1 3 4 3 6 -2 4 7 (2) (1) (3) (4) (5)
В дальнейшем 1-я строка не подлежит изменению!
2) Сформируем нули во 2-й и 3-й строках первого столбца. Для этого умножим 1-ю строку на 1-й элемент 2-й строки и вычтем из 2-й строки. Так же поступим с 3-й строкой. (Множители указаны в [ ].)
1 3 -2 3 5 0 -1 3 -3 - 6 [ -1] 0 -3 4 -5 -8 (2) (1) (3) (4) (5)
В дальнейшем 1-й столбец не подлежит изменению!
3) Превратим в «1» 2-й элемент на главной диагонали, то есть стоящий во 2-й строке и 2-ом столбце. В нашем примере достаточно умножить на (-1) вторую строку. (В общем случае следует поделить 2-ю строку на этот элемент. Если же он равен 0, то предварительно переставляют строки не трогая 1-й (!), или столбцы не трогая 1-й (!).)
1 3 -2 3 5 0 1 - 3 3 6 [ 3 ] 0 -3 4 -5 -8 (2) (1) (3) (4) (5) В дальнейшем 2-я строка не подлежит изменению!
4) Превратим в «0» 3-й элемент 2-го столбца. Для этого умножим 2-ю строку на (+3) и сложим с 3-ей. [ 1 3 -2 ] 3 5 [ 0 1 - 3 ] 3 6 [ 0 0 - 5 ] 4 10 (2) (1) (3) (4) (5)
Под главной диагональю стоят нули, а на самой главной диагонали их нет. Этот вид и является каноническим. (В других вариантах 3-я строка, или даже 2-я и 3-я вместе, могут состоять из одних нулей.) Минор, содержащий ненулевые элементы главной диагонали, является базисным, (здесь он указан скобками [ ]), а исходные номера входящих в него столбцов: (2) (1) (3) -- определяют номера базисных неизвестных; остальные неизвестные – свободные, и члены уравнений, содержащие их, переносят в правую часть.
5) Полученный вид матрицы и деление неизвестных на базисные и свободные позволяют переписать систему так:
x2 + 3x1 -- 2x3 = -- 3x4 -- 5x5 x1 -- 3x3 = -- 3x4 -- 6x5 -- 5x3 = -- 4x4 -- 10x5
и выразить базисные неизвестные через свободные:
x3 = (4/5) x4 + 2x5 x1 = 3x3 – 3x4 – 6x5 = (- 3/5) x4 x2 = -- 3x1 + 2x3 – 3x4 – 5x5 = (2/5) x4 – x5
6) Полученное решение представим в виде линейной комбинации столбцов фундаментальной системы решений, образующей базис в линейном пространстве решений. Таких столбцов столько, сколько свободных неизвестных (здесь = 2).Проще всего последовательно придать одной из свободных неизвестных произвольное ненулевое значение, а остальные свободные неизвестные принять нулями. В нашем примере удобно взять
1. x4 (1) = 5, x5 (1) = 0. Тогда x1 (1) = - 3, x2 (1) = 2, x3 (1) = 4 2. x4 (2) = 0, x5 (2) = 1. Тогда x1 (2) = 0, x2 (2) = - 1, x3 (2) = 2
Теперь общее решение можно записать так: x = C1 x (1) + C2 x (2). (Здесь С1, С2 – произвольные постоянные), или развернуто:
[x1] = [ - 3 ] [ 0 ] [x2] = [ 2 ] [ - 1 ] [x3] = C1 [ 4 ] + C2 [ 2 ] [x4] = [ 5 ] [ 0 ] [x5] = [ 0 ] [ 1 ]
Полезно проверить, что столбцы x (1), x (2) являются частными решениями исходной системы, то есть сделать прямую подстановку.
Сформулируем ответ на вопрос задачи: размерность пространства решений равна числу свободных неизвестных, (т.е. 2), а базисом в этом пространстве могут служить два найденных частных решения: x (1), x (2). 6. Дано уравнение кривой 2-го порядка. Найти собственные значения и собственные векторы матрицы соответствующей квадратичной формы и использовать их для приведения уравнения кривой к каноническому виду. Указать тип кривой.
6.1. –x2 – y2 +4xy + 2x – 4y + 1 = 0 6.2. 2x2 + 2y2 -- 2xy -- 2x – 2y + 1 = 0 6.3. 2xy + 2x – 2y = 0 6.4. -- 2x2 -- 2y2 +2xy -- 6x + 6y + 3 = 0 6.5. – 3x2 –3y2+4xy-- 6x+ 4y+2= 0 6.6. -- 2xy -- 2x – 2y + 1 = 0 6.7. –x2 – y2 -- 4xy -- 4x – 2y +2= 0 6.8. --4x2 -- 4y2 +2xy +10x--10y +1=0 6.9. 2xy + 2x – 2y -- 1 = 0 6.10. x2 + y2 + 2xy -- 8x – 8y + 1 = 0 6.11. x2 + y2 + 4xy -- 8x – 4y +1 = 0 6.12. x2 + y2 -- 2xy -- 2x + 2y -- 7 = 0 6.13. 2xy + 2x + 2y -- 3 = 0 6.14. 4x2 + 4y2 +2xy+12x + 12y +1 = 0 6.15. 3x2+3y2+4xy +8x +12y + 1 = 0 6.16. x2 + y2-- 8xy -- 20x + 20y + 1 = 0 6.17. 3x2+3y2-- 2xy--6x + 2y + 1 = 0 6.18. 4xy + 4x + 4y + 1 = 0 6.19. 3x2+3y2--4xy + 6 –4y -- 7 = 0 6.20. -- 2xy -- 2x + 2y + 3 = 0 6.21. 2x2 + 2y2 +4xy +8x +8y +1 =0 6.22 x2 + y2 – 4xy +4x – 2y +1 = 0 6.23 3x2 + 3y2 – 4xy +4x +4y +1 = 0 6.24 -4xy + 8x +8y +1 = 0
Рассмотрим пример 5x2 + 5y2 -- 2xy + 10x – 2y + 1 = 0 1) Выпишем симметричную матрицу квадратичной формы
5x2 + 5y2 -- 2xy: A= [ 5 -1] [-1 5 ]
2) Находим собственные значения:
Корни характеристического уравнения
3) Найдем собственные векторы матрицы А, рассматривая однородную систему: (5 – – u1 + (5 – При u (1) = (1; 1)T. (Знак (Т) означает транспонирование.) Нормируем его:
(Напомним: если u = (u1, u2)T, то | u | = При e (2)= u (2) / | u (2) |=(1; -1)T /
4) Сделаем замену координат
В новых координатах квадратичная форма примет вид
5x2 + 5y2 -- 2xy = l1x12 + l2 y12 = 4x12 + 6y12. Это следует из общей теории, но полезно использовать равенство (A x, x) = (AS x 1, S x 1) = (S TAS x 1, x 1) = ( A 1 x 1, x 1), откуда A1 =S TAS = diag(l1 , l2) = и проверить результат непосредственным матричным умножением. В новых координатах уравнение кривой примет вид: 4x12 + 6y12 + 5
7) Параллельным переносом осей координат устраним линейные члены. Соберем члены, содержащие x 1 и выделим полный квадрат: Аналогично поcтупим с членами, содержащими y1: Делаем замену переменных: x2 = x1 + в результате которой уравнение кривой принимает вид 4x2 2 + 6y2 2 – 4 = 0, и после деления на свободный член получаем
|

 в полярной системе координат. Требуется:
в полярной системе координат. Требуется: =0 до
=0 до  с шагом
с шагом  Det (A –
Det (A –  E) =
E) = 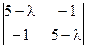 = (5 – l)2 – 1 = 0
= (5 – l)2 – 1 = 0 =(1; 1)T /
=(1; 1)T /  .
. .)
.)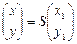 , где матрица перехода S имеет столбцами нормированные собственные векторы e (1), e (2) , то есть
, где матрица перехода S имеет столбцами нормированные собственные векторы e (1), e (2) , то есть  .
. .
.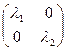 ,
, -- каноническое уравнение эллипса.
-- каноническое уравнение эллипса.


