Розспівався! - сердиться ватаг і наново перелічує карби.

Дата добавления: 2015-10-15; просмотров: 809

Метод интегрирования по частям базируется на следующей теореме:

Теорема 2. Пусть функция U = U(x) и V = V(x) дифференцируемы на некотором интервале (a;b). Пусть на (a;b) функция V(x)×U’(x) имеет первообразную. Тогда на (a;b) функция U(x)×V’(x) также имеет первообразную. При этом справедливо равенство:

.

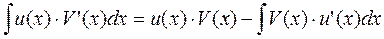Доказательство. По форме дифференцирования:

(U(x)×V(x))’ = U’(x)×V(x) + U(x)×V’(x).

По свойству неопределенного интеграла:

.

Тогда можно записать:

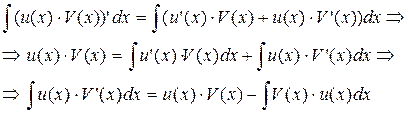
Замечание 1. Определение дифференциала и свойства инвариантности его формы позволяют переписать формулу интегрирования по частям в более короткой форме:

.

Замечание 2. Для успешного вычисления интеграла необходимо разумно разбить подинтегральное выражение на два множителя u(x) и dV(x) так, чтобы интеграл 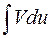оказался легко интегрируемым.

Практика показывает, что большая часть интегралов, берущихся с помощью метода интегрирования по частям может быть разбита на следующие три группы.

1) К первой группе относятся интегралы, у которых подынтегральная функция содержит в качестве множителя одну из следующих функций:

Ln x; arcsin x; arcos x; arctg x; arcctg x; ln²x; lnj(x); arcsin²x;…

при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции.

Тогда за функцию u(x) берут соответствующую из перечисленных.

2) Ко второй группе относятся интегралы вида

, ,

, ,

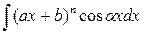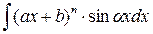где a,b,a, ,A – некоторые постоянные числа, A > 0, n Î N.

При этом в качестве u(x) следует брать (ax +b)ⁿ и интегрировать по частям n раз.

3) К третьей группе относятся интегралы вида:

, , ,

, , ,

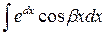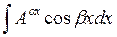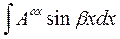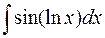где a, b, A – постоянные числа, A > 0, A # 1.

Такие интегралы берутся двукратным интегрированием по частям при любом выборе u(x). Это приводит к линейному уравнению относительно предложенного интеграла, откуда его и находят.

Замечание. Указанные три группы не исчерпывают всех без исключения интегралов, берущихся методом интегрирования по частям.