МЕТОДИКА ВИВЧЕННЯ ГРАМАТИКИ І ЛЕКСИКИ

Дата добавления: 2015-10-19; просмотров: 1583

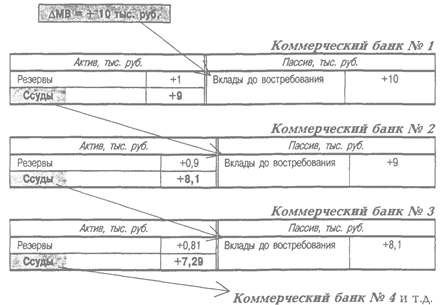
Рис.7.1. Изменение балансов банковской системы в процессе мультипликации вкладов (случай 1)

Ø Случай1.

Предположим, что:

а) население настолько ценит удобства, связанные с владением чековой книжкой, что все попадающие к нему наличные деньги стремится сразу же положить на счет до востребования;

б) коммерческие банки полагают минимальную резервную норму достаточной для поддержания необходимого уровня платежеспособности и не стремятся держать избыточных резервов, используя весь свой ссудный потенциал полностью для выдачи кредитов.

Пусть центральный банк расширил денежную базу, осуществив дополнительную эмиссию средств в размере 10 тыс. руб. (рис. 7.1). При этом наличная составляющая денежной массы возросла на ту же величину. Значит, первое расширение предложения денег будет произведено центральным банком на сумму.

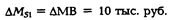
Предположим для простоты, что все получатели этих денег вносят их на вклады до востребования в один и тот же коммерческий банк №1. При норме обязательного резервирования, равной 10% от суммы вкладов, коммерческий банк №1 может выдать дополнительную ссуду на сумму 10тыс.руб.х(1 – 0,1)= 9 тыс. руб. Именно на эту величину расширит денежную массу данный банк:

Получатель ссуды в 9 тыс. руб. в коммерческом банке №1 скорее всего потратит эти деньги на покупку или на возврат долга. Получатель платежа, в свою очередь, вложит полученные средства в коммерческий банк №2. Объем вкладов до востребования в банке №2 увеличится на 9 тыс. руб., и он сможет выдать дополнительную ссуду в размере 9 тыс. руб. х (1 – 0,1) = 8,1 тыс. руб. На эту величину и расширит денежную массу банк №2:

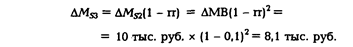
Аналогичным путем полученная в коммерческом банке №2 ссуда попадет на вклад до востребования в коммерческий банк №3. Объем вкладов до востребования в банке №3 увеличится на 8,1 тыс. руб., и он сможет выдать дополнительную ссуду в размере 8,1 тыс. руб. х (1 – 0,1) = 7,29 тыс. руб. На эту величину расширит денежную массу банк №3:

и т.д. до тех пор, пока все дополнительно выпущенные центральным банком 10 тыс. руб. не вернутся в центральный банк в виде обязательных резервов участвующих в этом процессе коммерческих банков.

В общем виде:

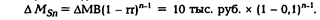
По окончании процесса суммарный прирост предложения денег составит:

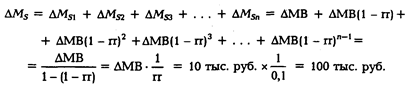
Следовательно, по окончании процесса 10 тыс. руб. наличных денег, созданных центральным банком, будут выведены из обращения и окажутся в фонде обязательных резервов банковской системы, а в обращении останется 100 тыс. руб. кредитных денег (вкладов до востребования).

Таким образом, увеличение денежной базы приводит к многократному (мультипликационному) расширению вкладов в коммерческих банках и денежной массы.

Депозитный (кредитный) мультипликатор показывает, во сколько раз конечный прирост денежной массы (предложения денег) превосходит первоначальный прирост денежной базы при отсутствии наличных денег в обращении и избыточных резервов.

Так как rr < 1, то депозитный мультипликатор всегда больше единицы.

Поскольку любое расширение денежной массы всегда является следствием расширения денежной базы, то

Однако такое определение предложения денег основано на малореалистичных предпосылках.

Ø Случай 2.

В более реалистичном виде:

1. Население обычно не вносит все попадающие к нему наличные деньги на банковский вклад, а часть их оставляет на руках в наличной форме (в форме кассовых остатков). Пропорция, в которой денежная масса распределена на кассовые остатки и вклады до востребования, описываетсякоэффициентом «наличность-депозиты»:

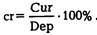
Тогда любой прирост денежной массы будет распределен между приростом кассовых остатков и приростом вкладов в определенной пропорции.

Поскольку и , то ;

Следовательно, если общий прирост денежной массы составил 1 рубль, то 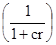копеек приходится на прирост вкладов до востребования и копеек — на прирост кассовых остатков.

2. Коммерческие банки обычно считают минимальную норму резервирования вкладов чересчур низкой для поддержания нормальной платежеспособности. К тому же обязательные резервы хранятся в центральном банке. Поэтому коммерческие банки, как правило, предпочитают часть своих избыточных резервов не отдавать в ссуду, а хранить в самом банке. Та доля вкладов, которую коммерческие банки в среднем считают необходимым хранить в виде избыточных резервов, называетсянормой избыточного резервирования вкладов:

где ERes — объем избыточных резервов.

При наличии избыточных резервов коммерческие банки используют для выдачи ссуд не весь свой ссудный потенциал, а за вычетом суммы хранящихся в банке избыточных резервов:

Тогда процесс мультипликации вкладов будет протекать по-другому. На каждом этапе из него будут исключаться не только обязательные, но и избыточные резервы, а также кассовые остатки. Поэтому итоговое расширение денежной массы будет меньше, чем в предыдущем случае.

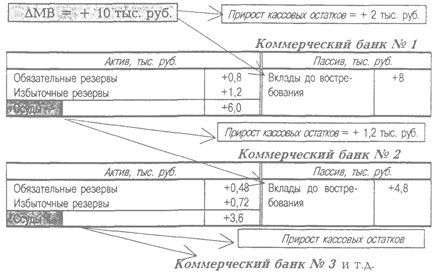
Рис. 7.2. Изменение балансов банковской системы в процессе мультипликации вкладов (случай 2)

Например (рис. 7.2), если сr = 0,25, еr = 0,15 и по-прежнему rr = 0,1, то при эмиссии дополнительных 10 тыс. руб. первое расширение денежной массы центральным банком будет таким же, как и в предыдущем случае:

Но теперь получатели этих денег оставят у себя 20% от полученной суммы в наличной форме:

и только 80%, т.е.

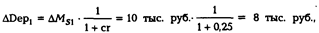будут внесены на вклады до востребования в коммерческий банк № 1.

Банк №1 поступит с этими деньгами следующим образом:

• 10%, т.е. DRRres = DDер • rr = 8 тыс. руб. • 0,1 = 0,8 тыс. руб., отправит в центральный банк для пополнения своих обязательных резервов;

• 15%, т.е. DERres = DDер • еr = 8 тыс. руб. • 0,15 = 1,2 тыс. руб., оставит в наличной форме для формирования избыточных резервов;

• оставшиеся после формирования резервного фонда 75% от суммы вклада выдаст в ссуду:

Прирост объема ссуд = DDер (1 – rr – cr) = 8 тыс. руб. (1 – 0,1 – 0,15) = 6 тыс. руб.

Следовательно, банк №1 увеличит денежную массу на 6 тыс. руб. (а не на 9 тыс. руб., как в предыдущем случае):

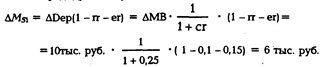
Из общей суммы ссуды банка №1 в коммерческий банк №2 попадет только 80% ее, и всего 75% от этого вклада будут выданы в кредит. Следовательно, банк №2 увеличит денежную массу на 3,6 тыс. руб. (а не на 8,1 тыс. руб., как в предыдущем случае):

и т.д. до тех пор, пока все дополнительно выпущенные центральным банком 10 тыс. руб. постепенно не выпадут из процесса мультипликации вкладов в виде кассовых остатков, обязательных резервов и избыточных резервов участвующих в этом процессе коммерческих банков.

В общем виде:

По окончании процесса суммарный прирост предложения денег составит:

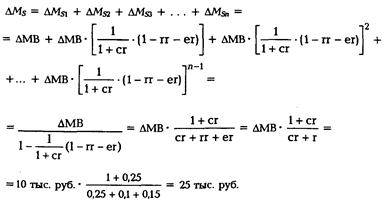
Суммарная норма резервирования вкладов, т.е. доля суммарных резервов (обязательных и избыточных) в объеме вкладов до востребования:

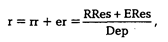
где r — суммарная норма резервирования вкладов.

Следовательно, по окончании процесса прирост денежной базы на 10 тыс. руб. приведет к увеличению денежной массы на 25 тыс. руб., а не на 100 тыс. руб., как в предыдущем случае.

Таким образом, наличие кассовых остатков у населения и избыточных резервов у коммерческих банков уменьшает масштаб мультипликативного расширения банковских вкладов и денежной массы (в нашем примере в 4 раза).

Денежный мультипликатор 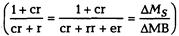показывает, во сколько раз конечный прирост денежной массы (предложения денег) превосходит первоначальный прирост денежной базы при наличии кассовых остатков у населения и избыточных резервов у коммерческих банков.

Так как (сr + r) < 1, то денежный мультипликатор всегда больше единицы.

Поскольку любое расширение денежной массы всегда является следствием расширения денежной базы, то при наличии кассовых остатков у населения и избыточных резервов у коммерческих банков:

<== предыдущая лекция | следующая лекция ==>

В МАЛОКОМПЛЕКТНІИ ШКОЛІ | МЕТОДИКА ФОРМУВАННЯ ГРАМАТИЧНИХ ПОНЯТЬ
1 | 2 | 3 | 4 | <== 5 ==> | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |