Будова формули
Будь-яка формула обов’язково починається зі знака “=”. Якщо про цей знак забути, то введене буде сприйнято як звичайний текст. Зрозуміло, що така формула працювати не буде. Основні правила для побудови формул такі: q формула записується тільки в рядок; q аргументи функцій обов’язково беруться в дужки; q дужки у формулах можуть бути тільки круглими; q аргументи функції відокремлюються один від другого комою; q знак множення у формулах пропускати не можна; q якщо у формулі використовується текст, то він має бути взятий у подвійні лапки. У таблиці в порядку спадання приорітету наведено знаки операцій, які можна використовувати у формулах.
До складу ЕТ входить надзвичайно велика кількість різноманітних стандартних функцій. Для ознайомлення з ними можна скористуватись спеціальним засобом, який називається Мастер функций. Основні стандартні елементарні математичні функції представлено в таблиці.
В наведених тригонометричних функціях використовується радіан як одиниця вимірювання величин кутів. Для знаходження логарифма числа за довільною основою використовується функція LOG(число, основание_логарифма). Досить часто у формулах ЕТ використовуються спеціальні функції, призначені для розв’язування типових розрахункових задач, зокрема, бухгалтерських. Щоб всі ці функції стали доступними в ЕТ, необхідно установити надбудову ЕТ, яка називається Пакет аналіза. Для цього треба виконати команду Сервис-Надстройки..., у діалоговому вікні Надстройки прокрутити Список надстроек: і відмітити в ньому пункт Пакет анализа. Наведемо найпростіші із спеціальних функцій. q Функція ЦЕЛОЕ (x) заокруглює число до найближчого меншого цілого. Наприклад, формула «= ЦЕЛОЕ (5.7)» дає результат 5, а формула «= ЦЕЛОЕ (-5.7)» дає результат 6. За допомогою цієї функції можна обчислити частку від ділення націло. Для цього спочатку треба виконати звичайне ділення, а потім заокруглити результат. Наприклад, формула «= ЦЕЛОЕ (23/3)» дає результат 7. q Функція ОСТАТ (число, делитель) обчислює остачу від ділення націло. Наприклад, формула «= ОСТАТ (23, 3)» дає результат 2. За допомогою розглянутих функцій можна записати загальне правило обчислення частки і остачі від ділення націло числа N на число D: N=D* ЦЕЛОЕ (N/D)+ ОСТАТ (N, D). q Розглянуті функції можна використовувати і для нецілих аргументів. Наприклад, формула «= ЦЕЛОЕ (8.6/2.3)» дає результат 3, а формула «= ОСТАТ (8.6, 2.3)» дає результат 1.7. Ці результати теж підпорядковані загальному правилу обчислення частки і остачі від ділення націло, тобто 8.6=3*2.3+1.7. q Функція заокруглення ОКРУГЛ(число, число_разрядов). Заокруглюється число, яке указано першим серед аргументів, за звичайним арифметичним правилом заокруглення (якщо цифра, яка відкидається, менша 5, то попередня цифра залишається без змін, у протилежному випадку попередня цифра збільшується на одиницю). Якщо число_разрядов більше нуля, то число заокруглюється до указаної кількості десяткових розрядів справа від десяткової крапки. Наприклад, якщо x=143.3184, то формула «= ОКРУГЛ (x, 2)» дає результат 143.32. Якщо число_разрядов дорівнює нулю, то число заокруглюється до найближчого цілого. Наприклад, якщо x=143.3184, то формула «= ОКРУГЛ (x, 0)» дає результат 143. Якщо число_разрядов менше нуля, то число заокруглюється до указаної кількості десяткових розрядів зліва від десяткової крапки. Наприклад, якщо x=143.3184, то формула «= ОКРУГЛ (x, -1)» дає результат 140. q Функції заокруглення ОКРУГЛВНИЗ(число, число_разрядов) і ОКРУГЛВВЕРХ(число, число_разрядов). Ці функції працюють, як і попередня, але заокруглюють тільки в ту сторону, яка указана в їх назві, тобто попередня цифра або тільки зменшується, або тільки збільшується. Наприклад, якщо x=143.3184, то формула «= ОКРУГЛВНИЗ (x, 2)» дає результат 143.31, а формула «= ОКРУГЛВВЕРХ (x, 1)» дає результат 143.4. q Функції заокруглення ОКРУГЛТ(число, множитель), ОКРВНИЗ(число, множитель) і ОКРВВЕРХ(число, множитель). Ці функції більш універсальні за попередні, оскільки дають можливість заокруглювати не тільки до степеня десяти, а по відношенню до довільного числа множитель. Внаслідок такого заокруглення число стає кратним множителю. Наприклад, формула «= ОКРУГЛТ (x, 1.2)» дає результат 4.8 при x=5.3, результат 6 при x=5.4 і результат 6 при x=5.5. Формула «= ОКРВНИЗ (x, 1.2)» дає результат 4.8 при всіх указаних x. Формула «= ОКРВВЕРХ (x, 1.2)» дає результат 6 при всіх указаних x. Аргументи цих функцій обов’язково повинні мати однаковий знак. Тут розглянуто лише деякі функції. Описи решти функцій треба шукати у вікні Справочная система, яке з’являється внаслідок виконання команди Справка-Вызов справки. В цьому вікні є вкладинка Предметный указатель, де спочатку треба ввести термін «функция», потім прокрутити отриманий список, вибрати потрібну функцію і натиснути клавішу < Enter>;. Крім арифметичних виразів, важливим компонентом формул є логічні вирази, зокрема, логічні функції. Логічний вираз – це є спільна назва для висловлювання та предиката. Висловлюванням називається твердження, відносно якого відразу можна зробити висновок, вірне воно чи ні. Наприклад, значенням висловлювання «7> 5» буде ИСТИНА. Значенням висловлювання «3> 5» буде ЛОЖЬ. Висловлювання, яке містить змінні величина, називається предикатом. В залежності від значень змінних предикат може набувати значення ИСТИНА або ЛОЖЬ. Наприклад, результатом порівняння «x> 3» буде ЛОЖЬ при x=2 і ИСТИНА — при x=6. Предикат утворюється внаслідок порівняння двох арифметичних виразів, з яких хоча б один містить змінні. У логічних виразах можуть використовуватись такі операції порівняння: «>» – більше, «> =» – більше або дорівнює, «<» – менше, «< =» – менше або дорівнює, «=» – дорівнює, «< >» – не дорівнює. Треба пам’ятати, що операції порівняння мають нижчий пріоритет, ніж арифметичні операції. У логічних виразах можуть використовуватись також логічні операції, реалізовані у вигляді логічних функцій: НЕ(x) - заперечення, И(x, y) - логічне множення, ИЛИ(x, y) - логічне додавання. Завдяки реалізації у вигляді функцій їх пріоритет не має значення. В арифметичних виразах логічне значення ИСТИНА поводить себе як число 1, а ЛОЖЬ – як число 0. І навпаки – в логічних виразах число 1 поводить себе як ИСТИНА, а число 0 – як ЛОЖЬ. Більше того, замість ИСТИНА можна указувати будь-яке число, відмінне від нуля. Логічні вирази найчастіше застосовуються як перший аргумент логічної функції ЕСЛИ: ЕСЛИ(лог_выражение, значение_если_истина, значение_если_ложь). Ця функція має три аргументи, зміст яких такий: якщо лог_выражение дорівнює ИСТИНА, то значення функції обчислюється як значення другого аргументу, а якщо лог_выражение дорівнює ЛОЖЬ, то значення функції обчислюється як значення третього аргументу. Специфіка функції ЕСЛИ полягає в тому, що її тип наперед не визначений і співпадає з типом або другого, або третього свого аргумента. Приклад 1. Задано число z. Побудувати формулу, яка дає результат z+1, якщо z> 1, і дає результат z у протилежному випадку. Розв’язок: «=ЕСЛИ(z> 1, z+1, z)». Приклад 2. Задано число z. Побудувати формулу, результатом якої є повідомлення «Перевищено порогове значення», якщо z> 100, і яка дає результат z у протилежному випадку. Розв’язок: «=ЕСЛИ(z> 100, “Перевищено порогове значення”, z)». Приклад 3. Задано число z. Побудувати формулу, яка дає результат z, якщо Розв’язок: «=ЕСЛИ(z< 10, 10, ЕСЛИ(z> 25, 25, z))». Основні повідомлення про помилки у формулах такі: q #ДЕЛ/0! – ділення на нуль. Таке повідомлення виникає в тих випадках, коли значення дільника операції ділення виявляється рівним нулю. q «Ошибка во введённом выражении». При цьому ЕТ пропонує варіант виправлення формули. Якщо ві погоджуєтесь із запропонованим, то натискуєте кнопку Да. Якщо ви натискуєте кнопку Нет, то це означає, що виправлення ви збираєтесь внести самостійно. q «Ошибка в формуле». Таке повідомлення може виникати в багатьох випадках. Наприклад, при введенні помилкової формули «=10+*2», в якій указано дві операції підряд. q «Несоответствие скобок». Таке повідомлення виникає в тих випадках, коли у введеній формулі порушено баланс між відкриваючими та закриваючими дужками. Наприклад: «=(2+3*4». q #ЗНАЧ! – помилка значення, що входить до складу формули. Може виникати, наприклад, тоді, коли вжито непрвильний відокремлювач між цілою та дробовою частинами числа. q #ИМЯ? – помилка в імені. Може виникати тоді, коли при обчисленні виразу q #ЧИСЛО! – помилка в аргументі функції. Наприклад, аргументи функції ОКРУГЛТ(число, множитель) обов’язково повинні мати однаковий знак. q #Н/Д – стандартне помилкове значення, яке означає НеДоступно. Правило тут таке: якщо хоча б один аргумент будь-якої функції або виразу дорівнює #Н/Д, то і значення цієї функції або виразу теж дорівнює #Н/Д. Розглянемо приклад обчислення за формулою. Відомо, що радіус описаного кола трикутника обчислюється за формулою Вправа 3.4.5. Обчислення за формулами. Ø Введіть у комірку A1 текст “Початкові дані: ”, а в комірку A5 — текст “Результати обчислень: ”. Ø Введіть у комірки A2, A3 і A4 тексти “a =”, “b =” і “c =” відповідно. Вирівнювання тексту в цих комірках установіть По правому краю. Таким чином, значення сторін трикутника будемо розташовувати в сусідніх комірках B2, B3 і B4 відповідно. Ø Введіть у комірки A6, A7 і A8 тексти “p =”, “S =” і “R =” відповідно. Вирівнювання тексту і в цих комірках установіть По правому краю. Отже, півпериметр, площу і радіус описаного кола будемо отримувати в сусідніх комірках B6, B7 і B8 відповідно. Ø Введіть у комірку B6 формулу “=(B2+B3+B4)/2”. Ø Введіть у комірку B7 формулу “=КОРЕНЬ(B6*(B6-B2)*(B6-B3)*(B6-B4))”. Ø Введіть у комірку B8 формулу “=B2*B3*B4/(4*B7)”. Ø Установіть для комірок B2, B3 і B4, а також для комірок B6, B7 і B8 вирівнювання По левому краю. Ø Виділіть всі ці комірки, клацніть по ним ПКМ, а в отриманому контекстному меню клацніть ЛКМ по пункту Формат ячеек.... В діалоговому вікні Формат ячеек виберіть вкладнику Число, в списку Числовые форматы: виділіть пункт Числовой, в лічильнику Число десятичных знаков: установіть значення 2 і натисніть кнопку OK. Ø У комірки B2, B3 і B4 введіть значення 3, 4 і 5 відповідно. В комірках B6, B7 і B8 ви повинні отримати значення 6.00, 6.00 і 2.50 відповідно. У розглянутій вправі ми з вами розв’язали пряму задачу. Дійсно, якщо зафіксувати, наприклад, значення сторін b, c, то можна сказати, що радіус описаного кола R є функцією сторони a, тобто R=f(a). Це означає, що змінюючи значення a, ми отримуємо різні значення результату R. Тепер подивимось на ту ж саму задачу з іншого боку: чи не можна, знаючи наперед значення результату R підібрати для нього відповідне значення сторони a. Така задача буде оберненою до даної. При цьому суттєво, що вивести формулу залежності a=f(R) практично неможливо. В ЕТ подібні задачі називаються задачами підбору параметра. Розв’язування задачі підбору параметра дозволяє знайти таке значення аргумента даної функції, при якому ця функція набуває заданого значення. Вправа 3.4.6. Підбір параметра. Знаходження значення сторони трикутника a для заданого радіуса R=3. Ø Установити курсор ЕТ на комірку B8, яка містить формулу для обчислення R. Ø Виконати команду Сервис-Подбор параметра.... Внаслідок цього на екрані з’являється діалогове вікно Подбор параметра. Ø Поле Установить в ячейке: цього вікна вже містить адресу B8 змінної R. Переконайтесь, що на відповідній комірці автоматично установився додатковий штриховий селектор. Якщо випадково він знаходиться в іншому місці, то його можна перемістити або за допомогою миші, або за допомогою курсорних клавіш. Ø Натискуючи клавішу < Tab>, перемістити текстовий курсор діалогового вікна в поле Значение:. Це можна зробити також, клацнувши в цьому полі ЛКМ. Ввести в це поле задане значення 3. Ø Натискуючи клавішу < Tab>, перемістити текстовий курсор діалогового вікна в поле Изменяя значение ячейки:. Це можна зробити також, клацнувши в цьому полі ЛКМ. Ø Ввести в це поле адресу комірки B2, яка містить значення сторони a. Це можна зробити також, клацнувши по цій комірці ЛКМ, або перемістивши в неї штриховий селектор курсорними клавішами. Ø Натиснути кнопку OK діалогового вікна. З’являється нове вікно Результат подбора параметра, в якому охарактеризовано процес пошуку рішення. Потрібне значення сторони a видно в самій комірці. Якщо користувача не задовольняє точність знайденого значення, то він може її змінити. Для цього треба виконати команду Сервис-Параметры..., у діалоговому вікні Параметры вибрати вкладинку Вычисления, а полі Относительная погрешность: цієї вкладинки ввести інше значення (наприклад, 0.00001 замість 0.001). Якими б універсальними та досконалими не були стандартні функції ЕТ, але вони не спроможні повністю вичерпати всі потреби користувача у розв’язуванні різноманітних задач. Саме тому табличний процесор має у своєму складі засоби для визначення користувачем власних функцій. Функції, визначені користувачем, створюються на об’єктно-орієнтованій мові програмування VBA (Visual Basic for Applications).
|


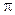
 , дає результат 10, якщо z< 10, і дає результат 25, якщо z> 25.
, дає результат 10, якщо z< 10, і дає результат 25, якщо z> 25. вжито неправильне найменування функції. Наприклад: «=КОРЕНЬ(tg(x)+1)». Правильне рішення: «=КОРЕНЬ(TAN(x)+1)».
вжито неправильне найменування функції. Наприклад: «=КОРЕНЬ(tg(x)+1)». Правильне рішення: «=КОРЕНЬ(TAN(x)+1)». , де a, b, c — його сторони, а площа трикутника
, де a, b, c — його сторони, а площа трикутника  при
при  .
.


