Закон Джоуля-ЛенцаДо кінця вільного пробігу електрони набувають під дією поля кінетичну енергію:
Згідно із зробленими припущеннями, уся ця енергія передається гратам при зіткненні і переходить в тепло. За час Δ t кожен електрон виконує Δ t/τ зіткнень. У провіднику перерізом S і довжини l знаходиться nS l електронів. Звідси витікає, що в провіднику за час Δ t виділяється кількість теплоти:
Кількість теплоти, що виділяється за одиницю часу в одиниці об'єму
Це співвідношення виражає закон Джоуля-Ленца. Таким чином, класична електронна теорія пояснює існування електричного опору металів, закони Ома і Джоуля-Ленца. Проте у ряді питань класична електронна теорія призводить до виводів, що знаходяться в протиріччі з дослідом. Ця теорія не може, наприклад, пояснити, чому молярна теплоємність металів, також як і молярна теплоємність діелектричних кристалів, дорівнює 3R, де R - універсальна газова стала (закон Дюлонга і Пти). Класична електронна теорія не може також пояснити температурну залежність питомого опору металів. Теорія дає ρ ~√ Т тоді як з експерименту виходить залежність ρ ~ T. Проте найбільш яскравим прикладом розбіжності теорії і дослідів є надпровідність. Згідно класичної електронної теорії, питомий опір металів повинен монотонно зменшуватися при охолодженні, залишаючись кінцевим при усіх температурах. Така залежність дійсно спостерігається на досліді при порівняно високих температурах. При нижчих температурах близько декількох кельвінів питомий опір багатьох металів перестає залежати від температури і досягає деякого граничного значення. Проте найбільший інтерес представляє явище надпровідності, відкрите данським фізиком Х. Каммерлинг-Оннесом в 1911 році. При деякій певній температурі Tкр, різній для різних речовин, питомий опір стрибком зменшується до нуля (рис. 3.32). Критична температура у ртуті дорівнює 4, 1 К, у алюмінію
Рисунок 3.32. Залежність питомого опору ρ від абсолютної температури T при низьких температурах: a - нормальний метал; b - надпровідник. Речовини в надпровідному стані мають виняткові властивості. Практично найбільш важливою з них є здатність тривалий час (багато років) підтримувати без загасання електричний струм, збуджений в надпровідному ланцюзі. Класична електронна теорія не здатна пояснити явище надпровідності. Пояснення механізму цього явища було дане тільки через 60 років після його відкриття на основі квантово-механічних представлень. Науковий інтерес до надпровідності зростав у міру відкриття нових матеріалів з вищими критичними температурами. Значний крок в цьому напрямі стався в 1986 році, коли було виявлено, що у одного складного керамічного з'єднання Tкр = 35 K. Вже в наступному 1987 року фізики зуміли створити нову кераміку з критичною температурою 98 К, що перевищує температуру рідкого азоту (77 К). Явище переходу речовин в надпровідний стан при температурах, що перевищують температуру кипіння рідкого азоту, було названо високотемпературною надпровідністю. У 1988 році було створено керамічне з'єднання на основі елементів Tl - Ca - Ba - Cu - O з критичною температурою 125 К. На 1 січня 2006 року рекорд критичної температури при нормальному тиску складає 138 К (з'єднання Hg - Ba - Ca - Cu - O(F), кераміка з частковим заміщенням кисню фтором, 2003 рік). При підвищенні тиску до 400000 атмосфер критична температура становила 166 К в тому ж з'єднанні. Нині ведуться інтенсивні роботи по пошуку нових речовин з ще вищими значеннями Tкр. Питання і завдання 1. Назвіть умови виникнення і існування електричного струму. 2. Що таке сторонні сили? Яка їх природа? 3. Що є причиною високої електропровідності металів? 4. Від чого залежить опір металевого провідника? 5. Запишіть закон Ома для однорідної і неоднорідної ділянки кола і для повного електричного кола? 6. У чому різниця між напругою і різницею потенціалів на ділянці електричного кола? 7. Визначите опір золотого дроту завдовжки 50 см і площею поперечного перерізу 0, 1мм2. Питомий опір золота 2, 2.10-8Ом.м. (11·10-4Ом). 8. Акумулятор, електрорушійна сила якого дорівнює 1, 5 В, замкнутий провідником, що має опір 3, 5 Ом. Знайти силу струму в колі, якщо внутрішній опір акумулятора 0, 5 Ом.(0, 375 А). 9. По провідникові, до кінців якого прикладена напруга 4 В, за 2 хв. Пройшов заряд 15 Кл. Знайти опір провідника.(32 Ом). 10. Два провідники опором 5 і 10 Ом підключені послідовно до джерела постійної напруги 100 В. Яка напруга на кожному провіднику? (33, 3 В, 66, 7 В). 11. Сила струму в провіднику рівномірно зростає от1 до 3 А, за 10с. Визначити заряд що пройшов через поперечний переріз провідника за цей час. (20 Кл). 12. Сила струму в провіднику рівномірно убуває від 3 А до 0, за 10с. Визначити заряд що пройшов через поперечний переріз провідника за цей час. (15 Кл). 13. 10 однакових ламп опором 400 Ом включені паралельно в мережу з напругою 220 В. Визначити силу струму в загальній частині кола. (5, 5 А). 14. На скільки рівних частин потрібно розділити провідник опором 100 Ом, щоб при паралельному з'єднанні цих частин отримати загальний опір 1 Ом? (10 частин). 15. Розрахувати струми I1, I2, I3 які течуть електричному колі (рис. 3.26), якщо 16. Знайти силу струму короткого замикання батареї, якщо при силі струму 2 А в зовнішньому колі виділяється потужність 24 Вт, а при силі струму 5 А - потужність 17. Заряд, що пройшов через поперечний переріз провідника опором 50 Ом за 2 секунди дорівнює 10 Кл. Яка кількість теплоти виділиться в провіднику за цей час? (2500 Дж). 18. Сила струму в провіднику опором 30 Ом міняється за лінійним законом від 0 до 10 А за 5 с. Яка кількість тепла виділиться в провіднику за цей час? (5000 Дж). 19. ЕРС батареї 12 В. При силі струму 4 А ККД батареї 50%. Визначити внутрішній опір джерела.(1, 5 Ом).
Магнітне поле і його характеристики. Магнітні явища були відомі ще у стародавньому світі. Компас був винайдений більше 4500 років тому. Він з'явився в Європі приблизно в XII столітті нової ери. Проте тільки в XIX столітті був виявлений зв'язок між електрикою і магнетизмом, і виникло уявлення про магнітне поле. Першими експериментами, що показали, що між електричними і магнітними явищами є глибокий зв'язок, були досліди данського фізика Х. Ерстеда (1820 р.). Ці досліди показали, що на магнітну стрілку, розташовану поблизу провідника із струмом, діють сили, які прагнуть повернути стрілку. У тому ж році французький фізик А. Ампер спостерігав силову взаємодію двох провідників із струмами і встановив закон взаємодії струмів. §49. Закон Ампера. Взаємодія паралельних струмів За сучасними уявленнями, провідники із струмом чинять силову дію один на одного не безпосередньо, а через магнітні поля, що оточують їх. Джерелами магнітного поля є рухомі електричні заряди (струми). Магнітне поле виникає в просторі, що оточує провідники із струмом, подібно до того, як в просторі, що оточує нерухомі електричні заряди, виникає електричне поле. Магнітне поле постійних магнітів також створюється електричними мікрострумами, циркулюючими усередині молекул речовини (гіпотеза Ампера). Магнітне поле струмів принципово відрізняється від електричного поля. Магнітне поле, на відміну від електричного, чинить силову дію тільки на рухомі заряди (струми). Для опису магнітного поля необхідно ввести силову характеристику поля, аналогічну вектору напруженості Е електричного поля. Такою характеристикою є вектор магнітної індукції В. Вектор магнітної індукції визначає сили, діючі на струми або заряди, що рухаються, в магнітному полі. За позитивний напрям вектора В приймається напрям від південного полюса S до північного полюса N магнітної стрілки, що вільно встановлюється в магнітному полі. Таким чином, досліджуючи магнітне поле, що створюється струмом або постійним магнітом, за допомогою маленької магнітної стрілки, можна в кожній точці простору визначити напрям вектора В.
Рисунок 3.33. Лінії магнітної індукції полів постійного магніту і котушки із струмом. Індикаторні магнітні стрілки орієнтуються по напряму дотичних до ліній індукції. Таке дослідження дозволяє представити просторову структуру магнітного поля. Аналогічно силовим лініям в електростатиці можна побудувати лінії магнітної індукції, в кожній точці яких вектор В спрямований по дотичній. Приклад ліній магнітної індукції полів постійного магніту і котушки із струмом приведений на рисунку 3.33. Зверніть увагу на аналогію магнітних полів постійного магніту і котушки із струмом. Лінії магнітної індукції завжди замкнуті, вони ніде не обриваються. Це означає, що магнітне поле не має джерел - магнітних зарядів. Силові поля, що мають цю властивість, називаються вихровими. Картину магнітної індукції можна спостерігати за допомогою дрібної залізної тирси, яка в магнітному полі намагнічується і, подібно до маленьких магнітних стрілок, орієнтуються уздовж ліній індукції. Для того, щоб кількісно описати магнітне поле, треба вказати спосіб визначення не лише напряму вектору але і його модуля. Найпростіше це зробити, вносячи в досліджуване магнітне поле провідник із струмом і вимірюючи силу, діючу на окрему прямолінійну ділянку цього провідника. Ця ділянка провідника повинна мати довжину Δ l, досить малу в порівнянні з розмірами областей неоднорідності магнітного поля. Як показали досліди Ампера, сила, діюча на ділянку провідника, пропорційна силі струму I, довжині Δ l цієї ділянки і синусу кута α між напрямами струму і вектора магнітної індукції: F = IBΔ l sin α. (3.48) Ця сила називається силою Ампера. Вона досягає максимального по модулю значення Fmax, коли провідник із струмом орієнтований перпендикулярно лініям магнітної індукції. Модуль вектора В дорівнює відношенню максимального значення сили Ампера, діючої на прямій провідник із струмом, до сили струму I в провіднику і його довжині Δ l:
У СІ за одиницю магнітної індукції прийнята індукція такого магнітного поля, в якому на кожен метр довжини провідника при силі струму 1 А діє максимальна сила Ампера 1 Н. Ця одиниця називається тесла (Тл).
Тесла - дуже велика одиниця. Індукція магнітного поля Землі приблизно дорівнює 0, 5·10-4 Тл. Великий лабораторний електромагніт може створити поле не більше 5 Тл.
Рисунок 3.34. Сила Ампера спрямована перпендикулярно вектору магнітної індукції В і напряму струму, що протікає по провіднику. Для визначення напряму сили Ампера використовують правило лівої руки: якщо розташувати ліву руку так, щоб лінії індукції В входили в долоню, а витягнуті пальці були спрямовані уздовж струму, то відведений великий палець вкаже напрям сили, діючої на провідник (рис. 3.34). Якщо кут α між напрямами вектора В і струму в провіднику відмінний від 90°, то для визначення напряму сили Ампера F зручніше користуватися правилом буравчика: уявний буравчик розташовується перпендикулярно площині, що містить вектор В і провідник із струмом, потім його руків'я обертається від напряму струму до напряму вектора В Поступальне переміщення буравчика показуватиме напрям сили Ампера (рис. 3.34). Одним з важливих прикладів магнітної взаємодії струмів є взаємодія паралельних струмів. Закономірності цього явища були експериментально встановлені Ампером. Якщо по двох паралельних провідниках електричні струми течуть в одну і ту ж сторону, то спостерігається взаємне притягання провідників. У разі, коли струми течуть в протилежних напрямах, провідники відштовхуються. Взаємодія струмів викликається їх магнітними полями: магнітне поле одного струму діє силою Ампера на інший струм і навпаки. Досліди показали, що модуль сили, діючої на відрізок завдовжки Δ l кожного з провідників, прямо пропорційний силам струму I1 і I2 в провідниках, довжині відрізку Δ l і обернено пропорційний до відстані R між ними:
У Міжнародній системі одиниць коефіцієнт пропорційності k дорівнює: k = μ 0/2π, де μ 0 - постійна величина, яку називають магнітною постійною. Її чисельне значення становить: μ 0 = 4π ·10-7 H/A2 ≈ 1, 26·10-6 H/A2. Для того, щоб при магнітній взаємодії паралельні струми притягувалися, а антипаралельні відштовхувалися, лінії магнітної індукції поля прямого провідника мають бути спрямовані за годинниковою стрілкою, якщо дивитися уздовж провідника по напряму струму. Для визначення напряму вектора В магнітного поля прямолінійного провідника також можна користуватися правилом буравчика: напрям обертання руків'я буравчика співпадає з напрямом вектору В якщо при обертанні буравчик переміщається у напрямі струму (рис. 3.35).
Рисунок 3.35. Рисунок 3.36. Рисунок 3.36 пояснює закон взаємодії паралельних струмів. Магнітна взаємодія паралельних провідників із струмом використовується в Міжнародній системі одиниць (СІ) для визначення одиниці сили струму - ампера: Ампер – сила постійного струму, який при проходженні по двом паралельним провідникам нескінченної довжини і малого кругового перерізу, розташованих на відстані 1 м один від одного у вакуумі, викликав би між цими провідниками силу магнітної взаємодії, рівну 2·10-7 H на кожен метр довжини. § 50. Закон Біо - Савара - Лапласа Магнітне поле постійних струмів різної конфігурації вивчалося експериментально французькими ученими Ж. Біо і Ф. Саваром (1820 р.). Результати цих дослідів були узагальнені французьким математиком і фізиком П. Лапласом. Вони дійшли висновку, що індукція магнітного поля струмів, що протікають по провіднику, визначається спільною дією усіх окремих ділянок провідника. Магнітне поле підпорядковується принципу суперпозиції: Якщо магнітне поле створюється декількома провідниками із струмом, то результуюча індукція є векторна сума індукцій полів, що створюються кожним провідником окремо. Індукцію B провідника із струмом можна представити як векторну суму елементарних індукцій dB створюваних окремими ділянками провідника. На досліді неможливо виділити окрему ділянку провідника із струмом, оскільки постійні струми завжди замкнуті. Можна виміряти тільки сумарну індукцію магнітного поля, що створюється усіма елементами струму. Закон Біо - Савара - Лапласа визначає вклад елементарної індукції dB в магнітну індукцію B результуючого магнітного поля в заданій точці, яке створюється малою ділянкою Δ l провідника із струмом I.
, бо в скалярному виді. (3.51)
Тут r - відстань від цієї ділянки d l до точки спостереження, α - кут між напрямом на точку спостереження і напрямом струму на цій ділянці. Напрям вектора dB визначається правилом буравчика.
Рисунок 3.37. Рисунок 3.37 ілюструє закон Біо-Савара- Лапласа на прикладі магнітного поля прямолінійного провідника із струмом. Якщо скласти (проінтегрувати) вклади в магнітне поле усіх окремих ділянок прямолінійного провідника із струмом, то вийде формула для магнітної індукції поля прямого струму:
(3.53) де R - радіус кругового провідника. Для визначення напряму вектора B також можна використовувати правило буравчика, тільки тепер його руків'я треба обертати у напрямі кругового струму, а поступальне переміщення буравчика вкаже напрям вектору магнітної індукції. § 51. Теорема про циркуляцію вектора індукції магнітного поля Розрахунки магнітного поля струмів часто спрощуються при врахуванні симетрії в конфігурації струмів, що створюють поле. В цьому випадку розрахунки можна виконувати за допомогою теореми про циркуляцію вектора магнітної індукції, яка в теорії магнітного поля струмів грає ту ж роль, що і теорема Гауса в електростатиці. Пояснимо поняття циркуляції вектора B. Нехай в просторі, де створено магнітне поле, вибраний деякий умовний замкнутий контур і вказаний позитивний напрям обходу контуру. На кожній окремій малій ділянці Δ l цього контуру можна визначити дотичну складову B l вектора B в цьому місці, тобто визначити проекцію вектора B на напрям дотичної до цієї ділянки контуру (рис. 3.38). Циркуляцією вектора B називають суму добутків B l ·Δ l, узяту по усьому контуру L, або інтеграл:
Рисунок 3.38. Замкнутий контур (L) із заданим напрямом обходу. Зображені струми I1, I2 і I3, що створюють магнітне поле. Деякі струми, що створюють магнітне поле, можуть пронизувати вибраний контур L в той час, як інші струми можуть знаходитися в стороні від контуру.
. (3.55)
В якості прикладу на рисунку 4.37 зображено декілька провідників із струмами, що створюють магнітне поле. Струми I2 і I3 пронизують контур L в протилежних напрямах, тому знаки у струмів повинні бути різні - позитивними вважаються струми, які пов'язані з вибраним напрямом обходу контуру правилом правого гвинта. Отже, I3 > 0, а I2 < 0. Струм I1 не пронизує контур L.
.
,
. Ця формула співпадає з виразом (3.52), отриманим із закону Біо-Савара-Лапласа. Цей приклад показує, що теорема про циркуляцію вектора магнітної індукції може бути використана для розрахунку магнітних полів, створюваних симетричним розподілом струмів, коли з міркувань симетрії можна " вгадати" загальну структуру поля. Є немало практично важливих прикладів розрахунку магнітних полів за допомогою теореми про циркуляцію. Одним з таких прикладів є завдання обчислення поля тороїдальної котушки (рис. 3.39).
Рисунок 3.39. Передбачається, що котушка щільна, тобто провід виток до витка намотаний на немагнітний тороїдальний сердечник. У такій котушці лінії магнітної індукції замикаються усередині котушки і є концентричними колами. Вони спрямовані так, що дивлячись уздовж них, ми побачили б струм у витках, циркулюючим за годинниковою стрілкою. Одна з ліній індукції деякого радіусу r1 ≤ r < r2 зображена на рисунку 3.39. Застосуємо теорему про циркуляцію до контуру L у вигляді кола, співпадаючого із зображеною на рисунку 3.39 з лінією індукції магнітного поля. З міркувань симетрії ясно, що модуль вектору В однаковий уздовж усієї цієї лінії. По теоремі про циркуляцію можна записати: B · 2 π r = μ 0IN, B · 2π r = μ 0IN,
. (3.56)
Таким чином, модуль вектора магнітної індукції в тороїдальній котушці залежить від радіусу r. Якщо сердечник котушки тонкий, тобто r2 - r1 < < r, то магнітне поле усередині котушки практично однорідне. Величина n = N/2π r є числом витків на одиницю довжини котушки. В цьому випадку B = μ 0In. (3.57) У цей вираз не входить радіус тора, тому воно справедливе і в граничному випадку На рисунку 3.40 зображено магнітне поле котушки кінцевої довжини. Слід звернути увагу на те, що в центральній частині котушки магнітне поле практично однорідне і значно сильніше, ніж поза котушкою. На це вказує густина ліній магнітної індукції. У граничному випадку нескінченно довгого соленоїда однорідне магнітне поле цілком зосереджене усередині соленоїда.
Рисунок 3.40. У разі нескінченно довгого соленоїда вираз для модуля магнітної індукції можна отримати безпосередньо за допомогою теореми про циркуляцію, застосувавши її до прямокутного контуру, показаного на рисунку 3.41.
Рисунок 3.41. Вектор магнітної індукції має відмінну від нуля проекцію на напрям обходу контуру abcd тільки на стороні ab. Отже, циркуляція вектора В по контуру рівна B l, де l - довжина сторони ab. Число витків соленоїда, що пронизують контур abcd, дорівнює n · l, де n - число витків на одиницю довжини соленоїда, а повний струм, що пронизує контур, рівний In l. Згідно з теоремою про циркуляцію, Bl = μ 0Inl, звідки B = μ 0In.
|


 .
. . (3. 47)
. (3. 47)
 1 =
1 = 
 . (3.49)
. (3.49)

 (3.50)
(3.50)



 . (3.52)
. (3.52)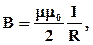 Закон Біо-Савара-Лапласа дозволяє розраховувати магнітні поля струмів різних конфігурацій. Неважко, наприклад, виконати розрахунок магнітного поля в центрі кругового витка із струмом. Цей розрахунок призводить до формули:
Закон Біо-Савара-Лапласа дозволяє розраховувати магнітні поля струмів різних конфігурацій. Неважко, наприклад, виконати розрахунок магнітного поля в центрі кругового витка із струмом. Цей розрахунок призводить до формули: . (3.54)
. (3.54)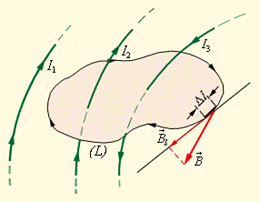
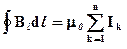 Теорема про циркуляцію стверджує, що циркуляція вектора B магнітного поля постійних струмів у вакуумі по будь-якому контуру L завжди дорівнює добутку магнітної сталої μ 0 на суму усіх струмів, що пронизують контур:
Теорема про циркуляцію стверджує, що циркуляція вектора B магнітного поля постійних струмів у вакуумі по будь-якому контуру L завжди дорівнює добутку магнітної сталої μ 0 на суму усіх струмів, що пронизують контур: Теорема про циркуляцію в цьому прикладі виражається співвідношенням:
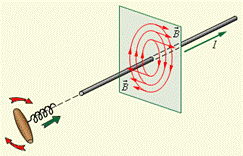
Теорема про циркуляцію в цьому прикладі виражається співвідношенням: Простим прикладом застосування теореми про циркуляцію є визначення магнітної індукції поля прямолінійного провідника із струмом. Враховуючи симетрію в цьому завданні, контур L доцільно вибрати у вигляді кола деякого радіусу R, що лежить в перпендикулярній провідникові площині. Центр кола знаходиться в деякій точці провідника. В силу симетрії вектор B спрямований по дотичній (B l · = B), а його модуль однаковий в усіх точках кола. Застосування теореми про циркуляцію призводить до співвідношення:
Простим прикладом застосування теореми про циркуляцію є визначення магнітної індукції поля прямолінійного провідника із струмом. Враховуючи симетрію в цьому завданні, контур L доцільно вибрати у вигляді кола деякого радіусу R, що лежить в перпендикулярній провідникові площині. Центр кола знаходиться в деякій точці провідника. В силу симетрії вектор B спрямований по дотичній (B l · = B), а його модуль однаковий в усіх точках кола. Застосування теореми про циркуляцію призводить до співвідношення: звідки слідує формула для модуля магнітної індукції поля прямолінійного провідника із струмом
звідки слідує формула для модуля магнітної індукції поля прямолінійного провідника із струмом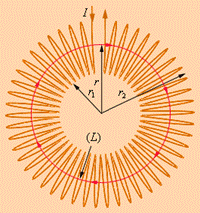
 де N - повне число витків, а I – сила струму, що протікає по витках котушки. Отже,
де N - повне число витків, а I – сила струму, що протікає по витках котушки. Отже,




