Пусть дана задача:  (1)
(1)
Определение. Пусть  – некоторый план задачи (1). Будем называть его обыкновенным, если вектора
– некоторый план задачи (1). Будем называть его обыкновенным, если вектора
 (6)
(6)
линейно независимы.
Теорема 3. Пусть  – обыкновенный локально-оптимальный план задачи (1). Тогда необходимо найдётся такой классический вектор Лагранжа
– обыкновенный локально-оптимальный план задачи (1). Тогда необходимо найдётся такой классический вектор Лагранжа 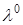 , причём единственный (он может быть нулевым), что выполняется условие:
, причём единственный (он может быть нулевым), что выполняется условие:
1. 
2. 
3.  .
.
Доказательство. Пусть  – обыкновенный локально-оптимальный план. В силу локальной оптимальности для него выполняется условие теорема 2, в частности, условия (4)-(5). Докажем, что в силу обыкновенности множитель
– обыкновенный локально-оптимальный план. В силу локальной оптимальности для него выполняется условие теорема 2, в частности, условия (4)-(5). Докажем, что в силу обыкновенности множитель  . Предположим противное, то есть
. Предположим противное, то есть  . Тогда из условия (4) получаем
. Тогда из условия (4) получаем
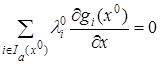 ,
,
в котором не все множители  нулевые. Тогда это означает линейную зависимость векторов (6) и противоречит обыкновенности
нулевые. Тогда это означает линейную зависимость векторов (6) и противоречит обыкновенности  .
.
Итак, 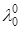 положительно. Разделим тогда выражение (5) на
положительно. Разделим тогда выражение (5) на 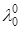 и переобозначим:
и переобозначим:  , тогда придём к условию
, тогда придём к условию  .
.
Условия 2 и 3 теоремы следуют из теоремы 2.
Докажем единственность 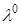 . Предположим противное. Найдётся ещё один вектор Лагранжа
. Предположим противное. Найдётся ещё один вектор Лагранжа  такой что
такой что 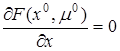 . Вычитая из этого равенства
. Вычитая из этого равенства 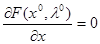 , придём к
, придём к 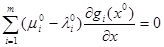 , причём не все коэффициенты
, причём не все коэффициенты  . Это означает линейную зависимость векторов (6) и снова противоречит обыкновенности
. Это означает линейную зависимость векторов (6) и снова противоречит обыкновенности  .
.
Ч.т.д.
Обсуждение. Теорема 2 и теорема 3 вместе приводят к принципу Лагранжа снятия ограничений в задаче (1), согласно которому и оптимальный план, и все локально оптимальные планы находятся среди решений систем
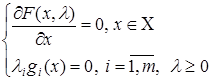 (7)
(7)
если они обыкновенные и
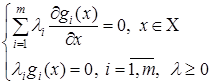 (8)
(8)
если  не является обыкновенным.
не является обыкновенным.
Каждая из систем (7) и (8) представляет собой систему  уравнений относительно неизвестных
уравнений относительно неизвестных 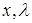 , то есть задача оптимизации сводится к алгебраической задаче.
, то есть задача оптимизации сводится к алгебраической задаче.
Определение. Задачу (1) будем называть нормальной, если оптимальный план у неё обыкновенный.
Большинство задач вида (1) являются нормальными. Более того, у большинства задач вида (1) все планы обыкновенные. В частности, ясно, что любой внутренний план является обыкновенным.
Определение. Решение системы (7) будем называть условно-стационарной точкой задачи (1).
Для нормальных задач принцип Лагранжа можно переформулировать:
Если  – локально-оптимальный план, то его нужно искать среди условно-стационарных точек задачи (1).
– локально-оптимальный план, то его нужно искать среди условно-стационарных точек задачи (1).
В случае линейных ограничений, то есть когда 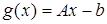 нетрудно доказать, что всегда справедливо классическое правило множителей Лагранжа без предположения обыкновенности
нетрудно доказать, что всегда справедливо классическое правило множителей Лагранжа без предположения обыкновенности  .
.

 (1)
(1) – некоторый план задачи (1). Будем называть его обыкновенным, если вектора
– некоторый план задачи (1). Будем называть его обыкновенным, если вектора (6)
(6)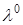 , причём единственный (он может быть нулевым), что выполняется условие:
, причём единственный (он может быть нулевым), что выполняется условие:

 .
. . Предположим противное, то есть
. Предположим противное, то есть  . Тогда из условия (4) получаем
. Тогда из условия (4) получаем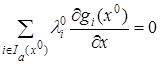 ,
, нулевые. Тогда это означает линейную зависимость векторов (6) и противоречит обыкновенности
нулевые. Тогда это означает линейную зависимость векторов (6) и противоречит обыкновенности 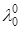 положительно. Разделим тогда выражение (5) на
положительно. Разделим тогда выражение (5) на  , тогда придём к условию
, тогда придём к условию 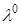 . Предположим противное. Найдётся ещё один вектор Лагранжа
. Предположим противное. Найдётся ещё один вектор Лагранжа  такой что
такой что 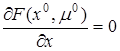 . Вычитая из этого равенства
. Вычитая из этого равенства 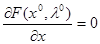 , придём к
, придём к 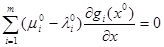 , причём не все коэффициенты
, причём не все коэффициенты  . Это означает линейную зависимость векторов (6) и снова противоречит обыкновенности
. Это означает линейную зависимость векторов (6) и снова противоречит обыкновенности 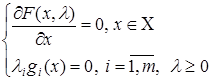 (7)
(7)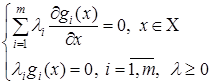 (8)
(8) уравнений относительно неизвестных
уравнений относительно неизвестных 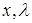 , то есть задача оптимизации сводится к алгебраической задаче.
, то есть задача оптимизации сводится к алгебраической задаче.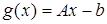 нетрудно доказать, что всегда справедливо классическое правило множителей Лагранжа без предположения обыкновенности
нетрудно доказать, что всегда справедливо классическое правило множителей Лагранжа без предположения обыкновенности 


