Пусть дана задача:  (1)
(1)
Определение. Пусть пара  – условно-стационарная точка задачи (1). Тогда
– условно-стационарная точка задачи (1). Тогда  ое ограничение задачи активное на
ое ограничение задачи активное на  будем называть жёстким, если
будем называть жёстким, если  и мягким или нежёстким, если
и мягким или нежёстким, если  .
.
Обозначим  ,
,  .
.
Ясно, что  .
.
Теорема 4 (Необходимое условие оптимальности второго порядка). Пусть  −обыкновенный локально-оптимальный план задачи (1),
−обыкновенный локально-оптимальный план задачи (1),  − соответствующий ему классический вектор Лагранжа. Тогда для любого вектора
− соответствующий ему классический вектор Лагранжа. Тогда для любого вектора  , удовлетворяющего системе
, удовлетворяющего системе
 (9)
(9)
квадратичная форма  .
.
Теорема 5 (Достаточное условие оптимальности второго порядка). Пусть  – условно-стационарная точка задачи (1), то есть решение системы (7). Тогда, если для любого вектора
– условно-стационарная точка задачи (1), то есть решение системы (7). Тогда, если для любого вектора  ,
,  и удовлетворяющего системе (9) квадратичная форма
и удовлетворяющего системе (9) квадратичная форма  , то
, то  – локально-оптимальный план задачи(1).
– локально-оптимальный план задачи(1).
Доказательство. Пусть выполнятся условия теоремы. Пусть  – компонента условно-стационарной точки, и для всякого допустимого направления квадратичная форма положительна. Предположим противное. Тем не менее,
– компонента условно-стационарной точки, и для всякого допустимого направления квадратичная форма положительна. Предположим противное. Тем не менее,  не является локально оптимальным планом. Это значит, для любой сколь угодно малой его окрестности найдутся планы лучшие, чем
не является локально оптимальным планом. Это значит, для любой сколь угодно малой его окрестности найдутся планы лучшие, чем  . Другими словами, существует последовательность
. Другими словами, существует последовательность  такая, что
такая, что  , где
, где  при
при  . Представим компоненты последовательности
. Представим компоненты последовательности  в виде
в виде  , причём
, причём  ,
,  при
при  . Так
. Так  представить нетрудно. Возьмём теперь вектор
представить нетрудно. Возьмём теперь вектор 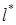 – предельный вектор последовательности
– предельный вектор последовательности  . Этот вектор существует, поскольку
. Этот вектор существует, поскольку  лежат на единичной сфере, то есть на компакте.
лежат на единичной сфере, то есть на компакте.
Рассмотрим разложение. Для 
 (10)
(10)
 (11)
(11)
Разделим выражения (10) и (11) справа на  и устремим
и устремим  к бесконечности. Тогда
к бесконечности. Тогда  и получим неравенства
и получим неравенства
 (12)
(12)
 (13)
(13)
Докажем, что наш вектор 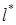 удовлетворяет системе (9), то есть является допустимым направлением. Из неравенства (12) следует, что неравенства из системы (9) на
удовлетворяет системе (9), то есть является допустимым направлением. Из неравенства (12) следует, что неравенства из системы (9) на 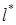 выполняются. Докажем, что выполняются и равенства из системы (9). Предположим противное, что найдётся такой номер
выполняются. Докажем, что выполняются и равенства из системы (9). Предположим противное, что найдётся такой номер  , что
, что  следовательно, соотношения
следовательно, соотношения  . Поскольку
. Поскольку  – условно-стационарная точка, то выполняется условие
– условно-стационарная точка, то выполняется условие  или можно записать так
или можно записать так  , так как
, так как  =0,
=0,  и
и  =0,
=0,  , то
, то  . Умножим это равенство скалярно на
. Умножим это равенство скалярно на 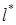 и сумму перенесём вправо, получим
и сумму перенесём вправо, получим
 .
.
Получили противоречие, следовательно, 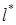 удовлетворяет всей системе (9).
удовлетворяет всей системе (9).
Рассмотрим равенства (10), (11). Умножим равенство (10) на множитель Лагранжа  , прибавим к (11) и добавим разложение
, прибавим к (11) и добавим разложение 
 , умноженное на
, умноженное на  =0. Если при этом сгруппировать множители при одинаковых степенях
=0. Если при этом сгруппировать множители при одинаковых степенях  , то получим
, то получим
 .
.
Разделим полученное неравенство на 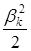 и устремим
и устремим 
 ,
,
то есть  . Это противоречит условиям теоремы.
. Это противоречит условиям теоремы.
Ч.т.д.
Теорема 4 и теорема 5 носят конструктивный характер. Их можно использовать для исключения точек, подозрительных на решение задачи (1), но не являющихся оптимальными. Для этого, как и в предыдущем параграфе, строятся некоторые задачи оптимизации (квадратичные).
Замечание. Если рассмотреть задачу  , то для неё теорема 4 и теорема 5 справедливы без предположения обыкновенности
, то для неё теорема 4 и теорема 5 справедливы без предположения обыкновенности  .
.
Если рассмотреть задачу со смешанными ограничениями  , то можно сформулировать принцип Лагранжа и условия оптимальности второго порядка простым совмещением результатов последних двух параграфов.
, то можно сформулировать принцип Лагранжа и условия оптимальности второго порядка простым совмещением результатов последних двух параграфов.
Векторная оптимизация. Эффективные планы. Усреднение целевых функций.
Мы рассматривали случай скалярной оптимизации, то есть целевая функция – скалярная величина. Однако на практике распространена ситуация, когда на одном и том же множестве требуется найти экстремум сразу нескольких целевых функций. Например, в производственной задаче наряду с максимизацией прибыли требуется минимизировать себестоимость продукции, максимизировать рентабельность производства, минимизировать расход некоторого важного ресурса и т.д.
Следовательно, возникает задача
 (1)
(1)
В задаче (1) требуется найти план, доставляющий минимум сразу  целевым функциям. Однако в описанной постановке эта задача является неопределённой, некорректной в том смысле, что для неё нельзя ввести определение оптимального плана. Суть в том, что в отличие от скалярного случая, когда два плана можно сравнивать между собой по целевой функции (какой лучше, какой хуже), в векторном случае это сделать не всегда возможно.
целевым функциям. Однако в описанной постановке эта задача является неопределённой, некорректной в том смысле, что для неё нельзя ввести определение оптимального плана. Суть в том, что в отличие от скалярного случая, когда два плана можно сравнивать между собой по целевой функции (какой лучше, какой хуже), в векторном случае это сделать не всегда возможно.
Пусть  =2 и даны два плана
=2 и даны два плана  такие что
такие что

По первой целевой функции лучше план  , а по второй –
, а по второй –  . А в целом эти планы не сравнимы в (1). Ситуация осложняется в том случае, когда целевые функции измеряются в различных масштабах, и в различных величинах (одна в килограммах, вторая в метрах, третья в рублях). Однако решить задачу каким-то образом нужно.
. А в целом эти планы не сравнимы в (1). Ситуация осложняется в том случае, когда целевые функции измеряются в различных масштабах, и в различных величинах (одна в килограммах, вторая в метрах, третья в рублях). Однако решить задачу каким-то образом нужно.
Определение. Скалярно-оптимальным планом задачи (1) по  ой целевой функции называется решение задачи
ой целевой функции называется решение задачи
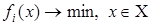 (2)
(2)
и будем его обозначать  .
.
Исключим из дальнейшего рассмотрения случай, когда  , то есть когда каждая из целевых функций задачи (1) достигает минимум на одном плане (в одной точке).
, то есть когда каждая из целевых функций задачи (1) достигает минимум на одном плане (в одной точке).
Определение. Говорят, что план  доминирует план
доминирует план  задачи (1), если выполняется неравенство
задачи (1), если выполняется неравенство  и существует хотя бы один номер
и существует хотя бы один номер  .
.
То есть один план доминирует другой, если он не хуже другого по всем целевым функциям и строго лучше хотя бы по одной.
Определение. План  называется эффективным или оптимальным по Парето, или не улучшаемым, если он не доминируется никаким другим планом задачи (1).
называется эффективным или оптимальным по Парето, или не улучшаемым, если он не доминируется никаким другим планом задачи (1).
Множество всех эффективных планов обозначим  . Ясно, какое определение не вкладывается в решение задачи (1), то есть в векторно-оптимальный план (его обозначают
. Ясно, какое определение не вкладывается в решение задачи (1), то есть в векторно-оптимальный план (его обозначают  ), он должен находиться среди эффективных, то есть задача (1) эквивалентна задаче:
), он должен находиться среди эффективных, то есть задача (1) эквивалентна задаче:
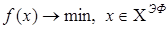 (3)
(3)
Но на практике множество  является достаточно широким, трудно строится для конкретной задачи. Лишь для задач линейно – векторной оптимизации существует алгоритм построения множества
является достаточно широким, трудно строится для конкретной задачи. Лишь для задач линейно – векторной оптимизации существует алгоритм построения множества  .
.
Рассмотрим следующие примеры.

 (1)
(1) – условно-стационарная точка задачи (1). Тогда
– условно-стационарная точка задачи (1). Тогда  ое ограничение задачи активное на
ое ограничение задачи активное на  будем называть жёстким, если
будем называть жёстким, если  и мягким или нежёстким, если
и мягким или нежёстким, если  .
. ,
,  .
. .
. − соответствующий ему классический вектор Лагранжа. Тогда для любого вектора
− соответствующий ему классический вектор Лагранжа. Тогда для любого вектора  , удовлетворяющего системе
, удовлетворяющего системе (9)
(9) .
. и удовлетворяющего системе (9) квадратичная форма
и удовлетворяющего системе (9) квадратичная форма  , то
, то  такая, что
такая, что  , где
, где  при
при  . Представим компоненты последовательности
. Представим компоненты последовательности  , причём
, причём  ,
,  при
при  представить нетрудно. Возьмём теперь вектор
представить нетрудно. Возьмём теперь вектор 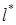 – предельный вектор последовательности
– предельный вектор последовательности  . Этот вектор существует, поскольку
. Этот вектор существует, поскольку  лежат на единичной сфере, то есть на компакте.
лежат на единичной сфере, то есть на компакте.
 (10)
(10) (11)
(11) и устремим
и устремим  к бесконечности. Тогда
к бесконечности. Тогда  и получим неравенства
и получим неравенства (12)
(12) (13)
(13) , что
, что  следовательно, соотношения
следовательно, соотношения  . Поскольку
. Поскольку  или можно записать так
или можно записать так  , так как
, так как  =0,
=0,  и
и  =0,
=0,  , то
, то  . Умножим это равенство скалярно на
. Умножим это равенство скалярно на  .
.
 .
.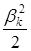 и устремим
и устремим  ,
, . Это противоречит условиям теоремы.
. Это противоречит условиям теоремы. , то для неё теорема 4 и теорема 5 справедливы без предположения обыкновенности
, то для неё теорема 4 и теорема 5 справедливы без предположения обыкновенности  .
. , то можно сформулировать принцип Лагранжа и условия оптимальности второго порядка простым совмещением результатов последних двух параграфов.
, то можно сформулировать принцип Лагранжа и условия оптимальности второго порядка простым совмещением результатов последних двух параграфов. (1)
(1) целевым функциям. Однако в описанной постановке эта задача является неопределённой, некорректной в том смысле, что для неё нельзя ввести определение оптимального плана. Суть в том, что в отличие от скалярного случая, когда два плана можно сравнивать между собой по целевой функции (какой лучше, какой хуже), в векторном случае это сделать не всегда возможно.
целевым функциям. Однако в описанной постановке эта задача является неопределённой, некорректной в том смысле, что для неё нельзя ввести определение оптимального плана. Суть в том, что в отличие от скалярного случая, когда два плана можно сравнивать между собой по целевой функции (какой лучше, какой хуже), в векторном случае это сделать не всегда возможно. такие что
такие что
 , а по второй –
, а по второй –  . А в целом эти планы не сравнимы в (1). Ситуация осложняется в том случае, когда целевые функции измеряются в различных масштабах, и в различных величинах (одна в килограммах, вторая в метрах, третья в рублях). Однако решить задачу каким-то образом нужно.
. А в целом эти планы не сравнимы в (1). Ситуация осложняется в том случае, когда целевые функции измеряются в различных масштабах, и в различных величинах (одна в килограммах, вторая в метрах, третья в рублях). Однако решить задачу каким-то образом нужно.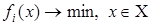 (2)
(2) .
. , то есть когда каждая из целевых функций задачи (1) достигает минимум на одном плане (в одной точке).
, то есть когда каждая из целевых функций задачи (1) достигает минимум на одном плане (в одной точке). доминирует план
доминирует план  задачи (1), если выполняется неравенство
задачи (1), если выполняется неравенство  и существует хотя бы один номер
и существует хотя бы один номер  .
. называется эффективным или оптимальным по Парето, или не улучшаемым, если он не доминируется никаким другим планом задачи (1).
называется эффективным или оптимальным по Парето, или не улучшаемым, если он не доминируется никаким другим планом задачи (1). . Ясно, какое определение не вкладывается в решение задачи (1), то есть в векторно-оптимальный план (его обозначают
. Ясно, какое определение не вкладывается в решение задачи (1), то есть в векторно-оптимальный план (его обозначают  ), он должен находиться среди эффективных, то есть задача (1) эквивалентна задаче:
), он должен находиться среди эффективных, то есть задача (1) эквивалентна задаче: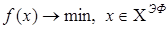 (3)
(3) .
.


