ЛИЗ Мера количества информации ТЕМА 5. ИНФОРМАЦИЯ И ЭНТРОПИЯ
Основные понятия и определения:
Ансамбль сообщений. Энтропия. Избыточность источника. Коэффициент сжатия.
6. Способы измерения информации Понятие количества информации естественно возникает, например, в следующих типовых случаях: 1. Равенство вещественных переменных a = b, заключает в себе информацию о том, что a равно b. Про равенство a2 = b2 можно сказать, что оно несет меньшую информацию, чем первое, т.к. из первого следует второе, но не наоборот. Равенство a3 = b3 несет в себе информацию по объему такую же, как и первое; 2. Пусть происходят некоторые измерения с некоторой погрешностью. Тогда чем больше будет проведено изме- рений, тем больше информации об измеряемой сущности будет получено; 3. М. о. некоторой сл. в. содержит в себе информацию о самой сл. в. Для сл. в., распределенной по нормальному закону, с известной дисперсией знание м.о. дает полную информацию 4. Рассмотрим схему передачи информации. Пусть передатчик описывается сл.в. X, тогда из-за помех в канале связи на приемник будет приходить сл.в. Y = X + Z, где Z | это сл.в., описывающая помехи. В этой схеме можно говорить о количестве информации, содержащейся в сл.в. Y, относительно X. Чем ниже уровень помех (дисперсия Z мала), тем больше информации можно получить из Y. При отсутствии помех Y содержит в себе всю информацию об X. В 1865 г. немецкий физик Рудольф Клаузиус ввел в статистическую физику понятие энтропии или меры уравно- вешенности системы. В 1921 г. английский математик Рональд Фишер впервые ввел термин \информация" в математическую стати- стику, но полученные им формулы носят очень специальный характер. В 1948 г. Клод Шеннон в своих работах по теории связи выписывает формулы для вычисления количества инфор- мация и энтропии. Термин энтропия используется Шенноном по совету патриарха компьютерной эры фон Неймана, отметившего, что полученные Шенноном для теории связи формулы для ее расчета совпали с соответствующими формулами статистической физики, а также то, что \точно никто не знает", что же такое энтропия. I Упражнение 4 Какое из соотношений несет в себе больше информации x = 5 или x > 3? 7. Вероятностный подход к измерению дискретной и непрерывной информации В основе теории информации лежит предложенный Шенноном способ измерения количества информации, содер- жащейся в одной сл.в. относительно другой сл.в. Этот способ приводит к выражению количества информации числом. Для д. с.в. X и Y, заданных законами распределения P(X = Xi) = pi, P(Y = Yj) = qj и совместным распределе- нием P(X = Xi; Y = Yj) = pij, количество информации, содержащейся в X относительно Y, равно I(X; Y) = X i;j pij log2 pij piqj : Для непрерывных сл. в. X и Y, заданных плотностями распределения вероятностей pX(t1), pY (t2) и pXY (t1; t2), аналогичная формула имеет вид I(X; Y) = Z R2 Z pXY (t1; t2) log2 pXY (t1; t2) pX(t1)pY (t2) dt1dt2: Очевидно, что P(X = Xi;X = Xj) = _ 0; при i 6= j P(X = Xi); при i = j и, следовательно, I(X;X) = X i pi log2 pi pipi = X i pi log2 pi: Энтропия д.с.в. X в теории информации определяется формулой H(X) = HX = I(X;X): Свойства меры информации и энтропии: 1) I(X; Y) > 0, I(X; Y) = 0, X и Y независимы; 2) I(X; Y) = I(Y;X); 3) HX = 0, X | константа; 4) I(X; Y) = HX + HY H(X; Y), где H(X; Y) = P i;j pij log2 pij; 5) I(X; Y) 6 I(X;X). Если I(X; Y) = I(X;X), то X | функция от Y.
8. Смысл энтропии Шеннона Энтропия д.с.в. | это минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной д.с.в. Рассмотрим пример (скачки). В заезде участвуют 4 лошади с равными шансами на победу, т. е. вероятность победы каждой лошади равна 1/4. Введем д.с.в. X, равную номеру победившей лошади. Здесь HX = 2. После каждого заезда по каналам связи достаточно будет передавать два бита информации о номере победившей лошади. Кодируем номер лошади следующим образом: 1|00, 2|01, 3|10, 4|11. Если ввести функцию L(X), которая возвращает длину сообщения, кодирующего заданное значение X, то м. о. ML(X) | это средняя длина сообщения, кодирующего X. Можно формально определить L через две функции L(X) = len(code(X)), где code(X) каждому значению X ставит в соответствие некоторый битовый код, причем, взаимно однозначно, а len возвращает длину в битах для любого конкретного кода. В этом примере ML(X) = HX. Пусть теперь д.с.в. X имеет следующее распределение P(X = 1) = ; P(X = 2) = ; P(X = 3) = P(X = 4) = ; т.е. лошадь с номером 1 | это фаворит. Тогда HX = log2 + log2 8 + log2 16 = log2 3 _ 1:186 бит/сим: Закодируем номера лошадей: 1|0, 2|10, 3|110, 4|111, | т. е. так, чтобы каждой код не был префиксом другого кода (подобное кодирование называют префиксным). В среднем в 16 заездах 1-я лошадь должна победить в 12 из них, 2-я | в 2-х, 3-я | в 1-м и 4-я | в 1-м. Таким образом, средняя длина сообщения о победителе равна (1 _ 12 + 2 _ 2 + 3 _ 1 + 3 _ 1)=16 = 1:375 бит/сим или м.о. L(X). Действительно, L(X) сейчас задается следующим распределением вероятностей: P(L(X) = 1) = 3=4, P(L(X) = 2) = 1=8, P(L(X) = 3) = 1=8. Следовательно, ML(X) = + + = = 1:375 бит/сим: Итак, ML(X) > HX. Можно доказать, что более эффективного кодирования для двух рассмотренных случаев не существует. То, что энтропия Шеннона соответствует интуитивному представлению о мере информации, может быть проде- монстрировано в опыте по определению среднего времени психических реакций. Опыт заключается в том, что перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия ис- пытаний, в которых каждая лампочка зажигается с определенной вероятностью pi ( PN i pi = 1), где i | это номер лампочки. Оказывается, среднее время, необходимое для правильного ответа испытуемого, пропорционально величине энтропии PN i=1 pi log2 pi, а не числу лампочек N, как можно было бы подумать. В этом опыте предполагается, что чем больше информации будет получено человеком, тем дольше будет время ее обработки и, соответственно, реакции на нее. I Упражнение 13 Найти энтропию д.с.в. X и среднюю длину каждого из приведенных кодов для этой д.с.в. X 1 3 4 5 6 p 0.4 0.2 0.1 0.2 0.1 code1(X) 000 001 010 011 111 code2(X) 0 100 101 110 111 code3(X) 00 01 110 10 111 code4(X) 0 10 1110 110 1111.
НОВ Теория информации и ее многочисленные приложения базируются на универсальной количественной мере информации, пригодной для сообщений любой природы. Получение информации о событиях, процессах или объектах, как правило, изменяет уровень наших знаний и понимания. Сообщение Предположение о том, что количество информации в сообщении
где Важнейшим свойством информации является аддитивность, т.е. ее количество в нескольких независимых сообщениях равно сумме количеств информации в каждом из них. Это легко показать, используя известное свойство вероятности произведения независимых событий. Так как совместная вероятность
то количество информации в этих сообщениях
Основание логарифма
В двоичных системах передачи информации используется лишь два символа, условно обозначаемых как 0 и 1. При независимых и равновероятных символах, когда
В случае ограниченного числа дискретных сообщений вводится понятие ансамблясообщений, - совокупности возможных сообщений и их вероятностей
Так как ансамбль сообщений образует полную группу событий, то
Если все сообщения равновероятны:
то количество информации в каждом из них равно
Имеющаяся до передачи сообщения неопределенность относительно того, какое конкретно из Пример. Пусть при передаче сообщений используется алфавит из
В связи с тем, что все буквы равновероятны
В простейшем случае двоичного кода ансамбль элементарных сообщений включает лишь два элемента: 0 и 1 (m = 2) и сообщение из n символов несет информацию
На практике при передаче сообщений неопределенность обычно снимается не полностью из-за шумов в канале передачи информации и связанных с ними ошибок. По принятому сигналу
|


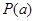 - вероятность сообщения. Так как
- вероятность сообщения. Так как  , то величина
, то величина  положительна и конечна. В случае
положительна и конечна. В случае 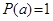 количество информации равно нулю.
количество информации равно нулю. независимых сообщений
независимых сообщений

 обычно принимают равным 2, и тогда количество информации выражается в двоичных единицах (“binary digit” - битах).
обычно принимают равным 2, и тогда количество информации выражается в двоичных единицах (“binary digit” - битах).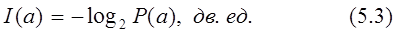
 , каждый из них несет одну двоичную единицу информации
, каждый из них несет одну двоичную единицу информации




 сообщений будет передаваться, после его приема исчезает. При этом, чем больше величина
сообщений будет передаваться, после его приема исчезает. При этом, чем больше величина  букв, если вероятности их появления одинаковы и они следуют независимо друг от друга. Количество информации при передаче одной буквы равно
букв, если вероятности их появления одинаковы и они следуют независимо друг от друга. Количество информации при передаче одной буквы равно
 и количество информации в каждой букве
и количество информации в каждой букве  . При независимом появлении букв количество информации в слове определяется соотношением
. При независимом появлении букв количество информации в слове определяется соотношением

 лишь с некоторой вероятностью
лишь с некоторой вероятностью  можно судить о том, что передавалось сообщение
можно судить о том, что передавалось сообщение  , т.е. после получения сообщения остается некоторая неопределенность.
, т.е. после получения сообщения остается некоторая неопределенность.


