Доверительные интервалы и доверительная вероятность, уровень значимости
Симплексный - передача данных только в одном направлении (телевидение, радио); Полудуплексный - прием и передача информации осуществляется поочередно (рация); Дуплексный - одновременные передача и прием данных (телефон). Дуплексный режим является наиболее скоростным режимом работы и позволяет эффективно использовать вычислительные возможности быстродействующих ЭВМ в сочетании с высокой скоростью передачи данных по каналам связи.
ЛЕКЦИЯ 5 Доверительные интервалы и доверительная вероятность, уровень значимости. Проверка статистических гипотез, критерии значимости, ошибки первого и второго рода. Построение доверительного интервала для математического ожидания непосредственно измеряемой величины. Распределение Стьюдента
Доверительные интервалы и доверительная вероятность, уровень значимости. Выборочные параметры распределения, определяемые по серии измерений, являются случайными величинами, следовательно, и их отклонения от генеральных параметров также будут случайными. Оценка этих отклонений носит вероятностный характер — при статистическом анализе можно лишь указать вероятность той или иной погрешности. Пусть для генерального параметра
Диапазон практически возможных значений ошибки, возникающей при замене
p = 1− β, (4.2) называемой уровнем значимости. Иначе выражение (4.1) можно интерпретировать как вероятность того, что истинное значение параметра а лежит в пределах
Вероятность β называется доверительной вероятностью и характеризует надежность полученной оценки. Интервал На практике обычно фиксируют значение доверительной вероятности (0,9; 0,95 или 0,99) и затем определяют доверительный интервал результата
Таким образом, если бы был известен закон распределения оценки Рассмотрим построение доверительного интервала для математического ожидания нормально распределенной случайной величины
Используя функцию Лапласа, получаем
Задавшись доверительной вероятностью β, определим по таблице функции Лапласа величину
Тогда доверительный интервал для математического ожидания принимает вид
или
Из (4.7) видно, что уменьшение доверительного интервала обратно пропорционально корню квадратному из числа опытов. Знание генеральной дисперсии позволяет оценивать математическое ожидание даже по одному наблюдению. Если для нормально распределенной случайной величины
где Закон распределения оценки 1) приближенный — при n ≥ 50 заменяют в выражении для
2) от случайной величины
|


 получена из опыта несмещенная оценка
получена из опыта несмещенная оценка  . Назначим достаточно большую вероятность
. Назначим достаточно большую вероятность  (такую, что событие с вероятностью
(такую, что событие с вероятностью  , для которого
, для которого
 . Большие по абсолютной величине ошибки будут появляться только с малой вероятностью
. Большие по абсолютной величине ошибки будут появляться только с малой вероятностью

 называется доверительным интервалом. Границы интервала
называется доверительным интервалом. Границы интервала  и
и  называются доверительными границами. Доверительный интервал при данной доверительной вероятности определяет точность оценки. Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра а внутри доверительного интервала: чем больше величина β, тем больше интервал
называются доверительными границами. Доверительный интервал при данной доверительной вероятности определяет точность оценки. Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра а внутри доверительного интервала: чем больше величина β, тем больше интервал  (и величина
(и величина  ). Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.
). Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.
 с известным генеральным стандартом
с известным генеральным стандартом  по выборке объемом
по выборке объемом 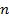 . Наилучшей оценкой для математического ожидания
. Наилучшей оценкой для математического ожидания  является среднее выборки x со стандартным отклонением среднего
является среднее выборки x со стандартным отклонением среднего


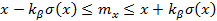

 , то доверительный интервал для математического ожидания при выбранной β имеет вид
, то доверительный интервал для математического ожидания при выбранной β имеет вид
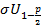 — квантиль стандартного нормального распределения.
— квантиль стандартного нормального распределения. и, в частности, от самого параметра
и, в частности, от самого параметра 
 , закон распределения которой не зависит от оцениваемого параметра
, закон распределения которой не зависит от оцениваемого параметра  и
и  обычно используются симметричные квантили
обычно используются симметричные квантили