Проверка статистических гипотез, критерии значимости, ошибки первого и второго рода
Под статистическими гипотезами понимаются некоторые предположения относительно распределений генеральной совокупности той или иной случайной величины. Под проверкой гипотезы понимают сопоставление некоторых статистических показателей, критериев проверки (критериев значимости), вычисляемых по выборке, с их значениями, определенными в предположении, что данная гипотеза верна. При проверке гипотез обычно подвергается испытанию некоторая гипотеза Чтобы решить вопрос о принятии или непринятии гипотезы, задаются уровнем значимости р. Наиболее часто используются уровни значимости, равные 0.10, 0.05 и 0.01. По этой вероятности, используя гипотезу о распределении оценки
Рис. 12. Критическая область Рис. 13. Проверка статистических гипотезы. гипотез.
Если найденное по выборке Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероятность такой ошибки не больше принятого уровня значимости. Ошибка второго рода состоит в том, что гипотеза принимается, а на самом деле она неверна. Вероятность этой ошибки тем меньше, чем выше уровень значимости, так как при этом увеличивается число отвергаемых гипотез. Если вероятность ошибки второго рода равна α, то величину (1 - α) называют мощностью критерия. На рис. 13 приведены две кривые плотности распределения случайной величины Обычно в качестве оптимального уровня значимости при проверке гипотез используют p = 0,05, так как если проверяемая гипотеза принимается с данным уровнем значимости, то гипотезу, безусловно, следует признать согласующейся с экспериментальными данными; с другой стороны, использование данного уровня значимости не дает оснований для отбрасывания гипотезы. Например, найдены два значения Например, р = 0,05 при двустороннем критерии соответствуют критические значения Θ0.025 и Θ0.975, т. е. значимыми (неслучайными) считаются Θ*, принявшие значения Θ* < Θ0.025 и Θ* > Θ0.975. При одностороннем критерии одно из этих неравенств заведомо невозможно (например, Θ* < Θ0.025) и значимыми будут лишь Θ* > Θ0.975. Вероятность последнего неравенства равна 0,025, и, следовательно, уровень значимости будет равен 0,025. Таким образом, если при одностороннем критерии значимости использовать те же критические числа, что и при двустороннем, этим значениям будет соответствовать вдвое меньший уровень значимости. Обычно для одностороннего критерия берут тот же уровень значимости, что и для двустороннего, так как при этих условиях оба критерия обеспечивают одинаковую ошибку первого рода. Для этого односторонний критерий надо выводить из двустороннего, соответствующего вдвое большему уровню значимости, чем тот, что принят. Чтобы сохранить для одностороннего критерия уровень значимости р = 0,05, для двустороннего необходимо взять р = 0,10, что дает критические значения Θ0.05 и Θ0.95. Из них для одностороннего критерия останется какое-нибудь одно, например, Θ0.95. Уровень значимости для одностороннего критерия равен при этом 0.05. Этому же уровню значимости для двустороннего критерия соответствует критическое значение Θ0.975. Но Θ0.95 < Θ0.975, значит, при одностороннем критерии большее число гипотез будет отвергнуто и, следовательно, меньше будет ошибка второго рода.
|

 в сравнении с альтернативной гипотезой
в сравнении с альтернативной гипотезой 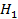 .
. (критерия значимости), находят квантильные доверительные границы, как правило, симметричные
(критерия значимости), находят квантильные доверительные границы, как правило, симметричные  и
и  . Числа
. Числа  и
и  образуют критическую область гипотезы (или область непринятия гипотезы) (рис. 12)
образуют критическую область гипотезы (или область непринятия гипотезы) (рис. 12)  .
.
 попадает между
попадает между  , соответствующие двум гипотезам
, соответствующие двум гипотезам  , то отвергается гипотеза
, то отвергается гипотеза  . Площадь под кривой плотности вероятности, соответствующей справедливости гипотезы Н0 вправо от значения
. Площадь под кривой плотности вероятности, соответствующей справедливости гипотезы Н0 вправо от значения  , равна уровню значимости р, т. е. вероятности ошибки первого рода. Площадь под кривой плотности вероятности, соответствующей справедливости гипотезы
, равна уровню значимости р, т. е. вероятности ошибки первого рода. Площадь под кривой плотности вероятности, соответствующей справедливости гипотезы  и
и  некоторого выборочного параметра, которые можно рассматривать как оценки генеральных параметров
некоторого выборочного параметра, которые можно рассматривать как оценки генеральных параметров  и
и  . Высказывается гипотеза, что различие между
. Высказывается гипотеза, что различие между  . Такая гипотеза называется нулевой, или нуль-гипотезой. Для ее проверки нужно выяснить, значимо ли расхождение между
. Такая гипотеза называется нулевой, или нуль-гипотезой. Для ее проверки нужно выяснить, значимо ли расхождение между  и проверяют, значимо ли ее отличие от нуля. Иногда удобнее рассматривать величину
и проверяют, значимо ли ее отличие от нуля. Иногда удобнее рассматривать величину  , сравнивая ее с единицей. Отвергая нулевую гипотезу, тем самым принимают альтернативную, которая распадается на две:
, сравнивая ее с единицей. Отвергая нулевую гипотезу, тем самым принимают альтернативную, которая распадается на две: 
 . Если одно из этих равенств заведомо невозможно, то альтернативная гипотеза называется односторонней, и для ее проверки применяют односторонние критерии значимости (в отличие от обычных, двусторонних). При этом необходимо рассматривать лишь одну из половин критической области (рис. 12).
. Если одно из этих равенств заведомо невозможно, то альтернативная гипотеза называется односторонней, и для ее проверки применяют односторонние критерии значимости (в отличие от обычных, двусторонних). При этом необходимо рассматривать лишь одну из половин критической области (рис. 12).


