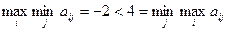Пример 5.3.1 -1.

Две компании А и В продают два вида лекарств против гриппа. Компания А рекламирует продукцию на радио (A1), телевидении (A2) и в газетах (A3). Компания В, в дополнение к использованию радио (В1) телевидения (В2) и газет (В3), рассы­лает также по почте брошюры (В4). В зависимости от умения и интенсивности проведения рекламной кампании, каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица характеризует процент клиентов, привлеченных или потерянных компанией А.

Решение игры основано на обеспечении наилучшего результата из наихудших для каждого игрока. Если компания А выбирает стратегию А1, то, независимо от того, что предпринимает компания В, наихудшим результатом является потеря компанией А 3% рынка в пользу компании В. Это определяется минимумом элементов первой строки матрицы платежей. Аналогично при выборе стратегии А2 наихудшим исходом для компании А является увеличение рынка на 5% за счет компании В. Наконец, наихудшим исходом при выборе стратегии А3 является потеря компанией А 9% рынка в пользу компании В. Эти результаты содержатся в столбце "Минимумы строк". Чтобы достичь наилучшего результата из наихудших компания А выбирает стратегию А2, так как она соответствует наибольшему элементу столбца "Минимумы строк".

Рассмотрим теперь стратегии компании В. Так как элементы матрицы являются платежами компании А, критерий наилучшего результата из наихудших для компании В соответствует выбору минимаксного значения. В результате приходим к выводу, что выбором компании В является стратегия В2.

Оптимальным решением игры является выбор стратегий А2 и В2, т.е. обеим компаниям следует проводить рекламу на телевидении. При этом выигрыш будет в пользу компании А, так как ее рынок увеличится на 5%. В этом случае говорят что цена игры равна 5% и что компании А и В используют стратегии, соответствующие седловой точке.

Решение, соответствующее седловой точке, гарантирует, что ни одной компании нет смысла пытаться выбрать другую стратегию. Действительно, если компания В переходит к другой стратегии (В1, В3 или В4), то компания А может сохранить свой выбор стратегии А2, кто приведет к большей потере рынка компанией B (6% или 8%). По тем же причинам компании А нет резона использовать другую стратегию, ибо если она применит, например, стратегию А3, то компания В может использовать свою стратегию В3 и увеличить свой рынок на 9%. Аналогичные выводы имеют место, если компания А будет использовать стратегию А1.

Однако не все игры двух участников с нулевой суммой являются вполне определенными. В общем случае можно лишь доказать, что максимин среднего платежа не превышает минимакса

.

Игры, в которых выполняется строгое неравенство, называются не полностью определенными играми без седловой точки. Пример такой игры, для которой

приведен на рис. 5.3.1-2.

Если игроки следуют изложенным ранее правилам, то игрок А выберет стратегию 1 и будет ожидать, что игрок В выберет стратегию 2, при которой проигрыш равен -2, в то время как игрок В изберет стра­тегию 3 и будет ожидать, что игрок А выберет стратегию 2 с выигрышем, равным 4. Однако результат а13 = 3 оказывается одинаково неожиданным для обоих игроков. На самом деле, если игрок В выберет свою третью страте­гию, то игрок А поступит правильнее, выбирая вторую, а не первую стратегию. Аналогично, если игрок А выберет первую стратегию, то игроку В выгоднее выбрать вторую стратегию, а не третью. По всей видимости, в играх такого типа принцип решения в той форме, как он изложен выше, оказывается непригодным.

Однако этот принцип решения остается верным, если расширить понятие стратегии за счет смешанных (или случайных) стратегий. Стратегии, рассматривавшиеся до сих пор, являлись чистыми. Смешанная стратегия представляет собой вероятностную комбинацию чистых стратегий, т. е. ряд чистых стратегий, взятых в случайном порядке с некоторыми вероятностями.