Преподаватель: Валентинов В.А.
Специальность: 080100.62 - Экономика
Группа: 1
Дисциплина: Эконометрика
Логин: 05ps1391776
Начало тестирования: 2013-02-18 00:35:27
Завершение тестирования: 2013-02-18 00:35:31
Продолжительность тестирования: 0 мин.
Заданий в тесте: 31
Кол-во правильно выполненных заданий: 0
Процент правильно выполненных заданий: 0 %
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Спецификация эконометрической модели
Для регрессионной модели вида  необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Отбор факторов, включаемых в модель множественной регрессии
При моделировании линейного уравнения множественной регрессии вида  необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

|
| | x1 и x2
|
|
|
| | y и { x1; x2 }
|
|
|
| | a и { b1; b2 }
|
|
|
| | b1 и b2
|
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 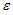 – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
– случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 110–119.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 35–41.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 74–89.
Порядина, О.В. Эконометрическое моделирование линейных уравнений регрессии: учеб. пособие для студентов специальностей 061800 "Мат. методы в экономике" и 351400 "Прикладная информатика (в экономике)" / О. В. Порядина. – Йошкар-Ола: МарГТУ, 2005. – С. 22–26.
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Фиктивные переменные
Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии:  ,
,
где  ,
, 
Частными уравнениями регрессии для кирпичного и монолитного являются …

|
| |  для типа дома кирпичный для типа дома кирпичный
|

|
| |  для типа дома монолитный для типа дома монолитный
|
|
|
| |  для типа дома кирпичный для типа дома кирпичный
|
|
|
| |  для типа дома монолитный для типа дома монолитный
|
Решение:
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие  ,
,  . Уравнение примет вид:
. Уравнение примет вид:  или
или  для типа дома кирпичный.
для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие  ,
,  . Уравнение примет вид
. Уравнение примет вид 
или  для типа дома монолитный.
для типа дома монолитный.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 167–182.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.190–195.
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Линейное уравнение множественной регрессии
Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение  . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

|
| | изменится на (-1,67)
|
|
|
| | увеличится на 1,67
|
|
|
| | уменьшится на (-1,67)
|
|
|
| | изменится на 0,003
|
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид  , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 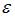 – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 53.
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Оценка параметров линейных уравнений регрессии
Величина  называется …
называется …

|
| | случайной составляющей
|
|
|
| | оценкой параметра
|
|
|
| | значением параметра
|
|
|
| | переменной
|
Решение:
Величина  называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 44.
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Предпосылки МНК, методы их проверки
Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле  , где
, где  – значение коэффициента автокорреляции остатков модели. Минимальная величина значения
– значение коэффициента автокорреляции остатков модели. Минимальная величина значения  будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.

|
| | положительной
|
|
|
| | отрицательной
|
|
|
| | нулевой
|
|
|
| | бесконечно малой
|
Решение:
Значение коэффициента автокорреляции остатков модели 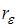 рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если 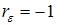 , то
, то  ; если
; если  , то
, то 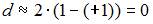 . Поэтому значение
. Поэтому значение  меняется от 0 до 4. Минимальное значение
меняется от 0 до 4. Минимальное значение  равно 0 для случая, когда
равно 0 для случая, когда  , то есть для положительной автокорреляции остатков.
, то есть для положительной автокорреляции остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 436 – 442.
Бывшев, В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008 – С 189 – 194.
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Состоятельность оценок параметров регрессии означает, что …

|
| | точность оценок выборки увеличивается с увеличением объема выборки
|
|
|
| | математическое ожидание остатков равно нулю
|
|
|
| | дисперсия остатков минимальная
|
|
|
| | дисперсия остатков не зависит от величины 
|
Решение:
Состоятельность оценок параметров регрессии означает, что точность оценок выборки увеличивается с увеличением объема выборки.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 60.
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Обобщенный метод наименьших квадратов (ОМНК)
При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.

|
| | обобщенный
|
|
|
| | косвенный
|
|
|
| | двухшаговый
|
|
|
| | трехшаговый
|
Решение:
При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется вместо традиционного метода наименьших квадратов применять обобщенный метод наименьших квадратов.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 150–160.
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Оценка тесноты связи
Коэффициент корреляции  парной линейной регрессии
парной линейной регрессии  нельзя рассчитать по формуле …
нельзя рассчитать по формуле …
Решение:
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции  Имеются разные модификации формулы линейного коэффициента корреляции, например
Имеются разные модификации формулы линейного коэффициента корреляции, например

Формула расчета  является ошибочной.
является ошибочной.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 59.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. С. 10–20.
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Оценка качества подбора уравнения
Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …

|
| | 0,9
|
|
|
| | 0,19
|
|
|
| | 0,81
|
|
|
| | 0,95
|
Решение:
Известно, что доля остаточной регрессии в общей составила 0,19. Значит,  Найдем коэффициент детерминации:
Найдем коэффициент детерминации:  Вычислим коэффициент корреляции:
Вычислим коэффициент корреляции: 
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 137.
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Проверка статистической значимости эконометрической модели
Для регрессионной модели известны следующие величины дисперсий:


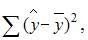 где y – значение зависимой переменной по исходным данным;
где y – значение зависимой переменной по исходным данным;  – значение зависимой переменной, вычисленное по регрессионной модели;
– значение зависимой переменной, вычисленное по регрессионной модели;  – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
Решение:
Назовем приведенные дисперсии:  – общая дисперсия;
– общая дисперсия;  – объясненная дисперсия;
– объясненная дисперсия;  – остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство:
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 
Эконометрика: учеб. / И. И. Елисеева [и др.]; под ред. И. И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 63-64.
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Оценка значимости параметров эконометрической модели
Проверка статистически значимого отличия от нуля оценок коэффициентов  линейной модели
линейной модели

осуществляется путем последовательного сравнения отношений 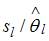 (
( –среднеквадратическая ошибка параметра
–среднеквадратическая ошибка параметра  ) с точкой, имеющей распределение …
) с точкой, имеющей распределение …

|
| | Стьюдента
|
|
|
| | Фишера
|
|
|
| | Дарбина – Уотсона
|
|
|
| | нормальное
|
Решение:
При проверке статистически значимого отличия от нуля оценок коэффициентов  линейной регрессионной модели
линейной регрессионной модели  выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии
выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии  модели рассчитывают отношение его среднеквадратической ошибки к значению оценки
модели рассчитывают отношение его среднеквадратической ошибки к значению оценки  . Полученное значение отношения
. Полученное значение отношения 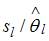 последовательно сравнивается с точкой, имеющей распределение Стьюдента.
последовательно сравнивается с точкой, имеющей распределение Стьюдента.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 73.
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Нелинейные зависимости в экономике
Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …

|
| | степенной функции
|
|
|
| | экспоненциальной функции
|
|
|
| | параболы второй степени
|
|
|
| | равносторонней гиперболы
|
Решение:
Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 89–92.
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Виды нелинейных уравнений регрессии
Степенной моделью не является регрессионная модель …
Решение:
Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: 


В уравнении 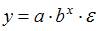 независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.
независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 77.
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной функции  может быть применен метод …
может быть применен метод …

|
| | логарифмирования и замены переменных
|
|
|
| | разложения функции в ряд Тейлора
|
|
|
| | потенцирования и замены переменных
|
|
|
| | обращения и замены переменных
|
Решение:
Функция  является внутренне линейной и с помощью логарифмирования может быть преобразована к виду
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду  , которая является линейной относительно логарифмов переменных. Сделав замену переменных
, которая является линейной относительно логарифмов переменных. Сделав замену переменных  ,
,  ,
, 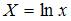 ,
,  , получим линейную функцию
, получим линейную функцию  . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Оценка качества нелинейных уравнений регрессии
Для регрессионной модели  , где
, где  – нелинейная функция,
– нелинейная функция, 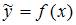 – рассчитанное по модели значение переменной
– рассчитанное по модели значение переменной  , получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной
, получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной  , равная …
, равная …
Решение:
Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R2. Значения индекса детерминации R2 и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением 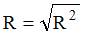 . Следовательно, значение
. Следовательно, значение  .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 99.
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Временные ряды данных: характеристики и общие понятия
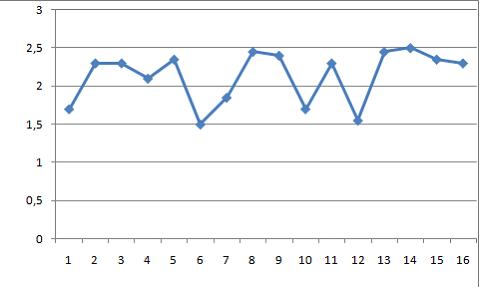
Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Решение:
График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 296–300.
Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.284–290.
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Структура временного ряда
Значение коэффициента автокорреляции первого порядка характеризует …

|
| | тесноту линейной связи
|
|
|
| | качество модели временного ряда
|
|
|
| | тесноту нелинейной связи
|
|
|
| | значимость тренда
|
Решение:
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 132–133.
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Аддитивная и мультипликативная модели временных рядов
Для аддитивной модели временного ряда Y = T + S + E сумма скорректированных сезонных компонент равна …

|
| |
|
|
|
| |
|
|
|
| | лагу
|
|
|
| | половине лага
|
Решение:
Для аддитивной модели временного ряда Y = T + S + E сумма скорректированных сезонных компонент равна нулю.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 312–316.
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для временного ряда известны характеристики:  – среднее и
– среднее и  – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …
Решение:
При моделировании временных рядов рассматривается отдельный класс – стационарные временные ряды. Основные характеристики стационарного временного ряда состоят в том, что среднее  и дисперсия стохастического процесса, сгенерировавшего конкретный временной, не зависят от времени t, то есть
и дисперсия стохастического процесса, сгенерировавшего конкретный временной, не зависят от времени t, то есть  ;
;  .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 335 – 336.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 284–288.
 ЗАДАНИЕ N 21 отправить сообщение разработчикам
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Модель равенства спроса и предложения, в которой предложение  является линейной функцией цены p, а спрос
является линейной функцией цены p, а спрос  является линейной функцией цены p и дохода y, состоит из уравнений …
является линейной функцией цены p и дохода y, состоит из уравнений …
Решение:
В модели предложение  является линейной функцией цены p. Значит, уравнение для предложения
является линейной функцией цены p. Значит, уравнение для предложения  будет иметь вид
будет иметь вид  . Спрос
. Спрос  является линейной функцией цены p и дохода y, значит, уравнение для спроса
является линейной функцией цены p и дохода y, значит, уравнение для спроса  будет иметь вид
будет иметь вид  . Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:
. Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:  .
.
Модель будет иметь вид
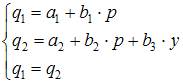
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 22 отправить сообщение разработчикам
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Классификация систем уравнений
Изучаются модели зависимости спроса  и предложения
и предложения  от цены p и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений.
от цены p и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений.
(1) 
(2) 
(3) 
|
|
| | система независимых уравнений
|
|
|
| | система одновременных уравнений
|
|
|
| | система рекурсивных уравнений
|
|
|
| | система приведенных уравнений
|
Решение:
В системе (1) оба уравнения зависят только от независимой переменной p. Это система независимых уравнений, и мы не предполагаем, что спрос  и предложение
и предложение  связаны между собой.
связаны между собой.
В системе (2) зависимые переменные спрос  и предложение
и предложение  содержатся и в правой, и в левой частях уравнения. Это система одновременных уравнений.
содержатся и в правой, и в левой частях уравнения. Это система одновременных уравнений.
В системе (3) первое уравнение содержит в правой части только независимую переменную p, а второе уравнение уже включает в себя и зависимую переменную  , определенную в первом уравнении. Это система рекурсивных уравнений.
, определенную в первом уравнении. Это система рекурсивных уравнений.
Система приведенных уравнений не является классом систем одновременных уравнений.
Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 23 отправить сообщение разработчикам
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Идентификация систем эконометрических уравнений
Дана приведенная форма модели системы одновременных уравнений: 
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 
(3) 
|
|
| | эндогенная переменная
|
|
|
| | экзогенная переменная системы
|
|
|
| | приведенный коэффициент
|
|
|
| | структурный коэффициент
|
Решение:
Рассмотрим каждое из обозначений.
(1)  – эндогенная переменная системы, входит в левую часть первого уравнения.
– эндогенная переменная системы, входит в левую часть первого уравнения.
(2)  – независимая переменная, то есть экзогенная переменная системы, входит в правую часть уравнений приведенной формы системы.
– независимая переменная, то есть экзогенная переменная системы, входит в правую часть уравнений приведенной формы системы.
(3)  – приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели).
– приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели).
Вариант ответа «структурный коэффициент» не является наименованием ни одного из обозначений; кроме этого, структурные коэффициенты содержатся в структурной форме модели, а в задании рассматривается приведенная форма модели.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–347.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–237.
 ЗАДАНИЕ N 24 отправить сообщение разработчикам
ЗАДАНИЕ N 24 отправить сообщение разработчикам
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
Если записать типы эконометрических моделей в следующем порядке:
1) точно идентифицируемая система одновременных уравнений,
2) сверхидентифицируемая система одновременных уравнений,
3) уравнение множественной регрессии,
4) уравнение множественной регрессии при автокорреляции остатков,
то методы, применяемые для нахождения параметров соответствующих типов эконометрических моделей, будут расположены в следующем порядке
|
|
| | косвенный метод наименьших квадратов
|
|
|
| | двухшаговый метод наименьших квадратов
|
|
|
| | метод наименьших квадратов
|
|
|
| | обобщенный метод наименьших квадратов
|
Решение:
Для нахождения структурных коэффициентов точно иденти

 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
 необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между … , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 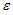 – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
– случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2. ,
, ,
, 
 для типа дома кирпичный
для типа дома кирпичный
 для типа дома монолитный
для типа дома монолитный
 для типа дома кирпичный
для типа дома кирпичный
 для типа дома монолитный
для типа дома монолитный
 ,
,  . Уравнение примет вид:
. Уравнение примет вид:  или
или  ,
,  . Уравнение примет вид
. Уравнение примет вид 
 . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта. , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 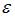 – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта.
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Коэффициентом регрессии является параметр bj. Его величина показывает, на сколько в среднем изменится зависимая переменная y, при изменении соответствующей независимой переменной xj на 1 единицу измерения. Таким образом, при изменении уровня безработицы на 1% среднедушевой денежный доход изменится на (-1,67) рубля при неизменной величине валового регионального продукта. называется …
называется … называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения.
называется случайной составляющей, или возмущением, и включает в себя влияние факторов, неучтенных в модели, ошибок выборки и ошибок измерения. , где
, где  – значение коэффициента автокорреляции остатков модели. Минимальная величина значения
– значение коэффициента автокорреляции остатков модели. Минимальная величина значения  будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.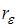 рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если 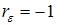 , то
, то  ; если
; если  , то
, то 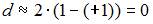 . Поэтому значение
. Поэтому значение  равно 0 для случая, когда
равно 0 для случая, когда  , то есть для положительной автокорреляции остатков.
, то есть для положительной автокорреляции остатков.
 парной линейной регрессии
парной линейной регрессии  нельзя рассчитать по формуле …
нельзя рассчитать по формуле …



 Имеются разные модификации формулы линейного коэффициента корреляции, например
Имеются разные модификации формулы линейного коэффициента корреляции, например
 является ошибочной.
является ошибочной. Найдем коэффициент детерминации:
Найдем коэффициент детерминации:  Вычислим коэффициент корреляции:
Вычислим коэффициент корреляции: 


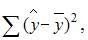 где y – значение зависимой переменной по исходным данным;
где y – значение зависимой переменной по исходным данным;  – значение зависимой переменной, вычисленное по регрессионной модели;
– значение зависимой переменной, вычисленное по регрессионной модели;  – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
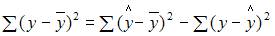
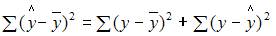

 – общая дисперсия;
– общая дисперсия;  – объясненная дисперсия;
– объясненная дисперсия;  – остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство:
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 
 линейной модели
линейной модели 
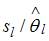 (
( –среднеквадратическая ошибка параметра
–среднеквадратическая ошибка параметра  ) с точкой, имеющей распределение …
) с точкой, имеющей распределение … модели рассчитывают отношение его среднеквадратической ошибки к значению оценки
модели рассчитывают отношение его среднеквадратической ошибки к значению оценки 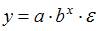






 может быть применен метод …
может быть применен метод … является внутренне линейной и с помощью логарифмирования может быть преобразована к виду
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду  , которая является линейной относительно логарифмов переменных. Сделав замену переменных
, которая является линейной относительно логарифмов переменных. Сделав замену переменных  ,
,  ,
, 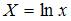 ,
,  , получим линейную функцию
, получим линейную функцию  . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных. , где
, где  – нелинейная функция,
– нелинейная функция, 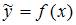 – рассчитанное по модели значение переменной
– рассчитанное по модели значение переменной  , получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной
, получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной 



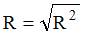 . Следовательно, значение
. Следовательно, значение  .
.


 – среднее и
– среднее и  – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …

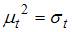

 ;
;  .
. является линейной функцией цены p, а спрос
является линейной функцией цены p, а спрос  является линейной функцией цены p и дохода y, состоит из уравнений …
является линейной функцией цены p и дохода y, состоит из уравнений …




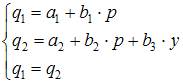







 – эндогенная переменная системы, входит в левую часть первого уравнения.
– эндогенная переменная системы, входит в левую часть первого уравнения. – независимая переменная, то есть экзогенная переменная системы, входит в правую часть уравнений приведенной формы системы.
– независимая переменная, то есть экзогенная переменная системы, входит в правую часть уравнений приведенной формы системы. – приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели).
– приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели).


