Реализация на matlab.

FEM.m

1. % U(x) выбрана x^3

2. clear

3. clc

4. a0=-3; %левая граница

5. a1=2; %правая граница

6. N=5; %количество узлов

7. h=(a1-a0)/(N-1); %шаг разбиения

8. X=a0:h:a1; %значения узлов

9. U1=-27; %значение в левой границе

10.Un=8; %значение в правой границе

11.d=zeros(N-2,1); %находим столбец-правую часть системы

12.for i=1:1:N-2

13. d(i)=1/h*(quadl(@(x) 6*x.*(x-X(i)),X(i),X(i+1))-quadl(@(x) 6*x.*(x-X(i+2)),X(i+1),X(i+2))); %6*x=(x^3)"

14.end

15.a=zeros(N-2); %задаем матрицу коэффициентов.

16.for i=1:1:N-2

17. a(i,i)=-2/h; %главная диагональ

18.end

19.for i=1:1:N-3

20. a(i,i+1)=1/h; %побочная правая

21.end

22.for i=2:1:N-2

23. a(i,i-1)=1/h; %побочная левая

24.end

25.c=a\d; %решаем систему

26.

27.g=1; %находим значения искомой функции в точках

28.X2=a0:h/g:a1;

29.for j=2:1:(N-1)*g

30. Y2(j)=vx(X2(j),a0,a1,U1,Un);

31. if (ceil(j/g)==0)

32. Y2(j)=Y2(j)+c(1)*fi1(X2(j),a0,h);

33. end

34. if (ceil(j/g)==N-1)

35. Y2(j)=Y2(j)+c(N-2)*fi2(X2(j),a1,h);

36. end

37. if (ceil(j/g)>0)&&(ceil(j/g)<N-1)

38. Y2(j)=Y2(j)+c(ceil(j/g)-1)*fi2(X2(j),X(ceil(j/g)+2),h)+c(ceil(j/g))*fi1(X2(j),X(ceil(j/g)+1),h);

39. end

40.

41.end

42.

43.Y2(1)=U1;

44.Y2(j+1)=Un;

45.pp=csape(X2,Y2);

46.hold on

47.grid on

48.fnplt(pp)

49.plot(X2,Y2,'g')

50.plot(X2,X2.^3,'r')

51.hold off

 

 

fi1.m

1. function F=fi1(x,xim,h)

2. F=(x-xim)/h;

 

 

fi2.m

1. function F=fi2(x,xip,h)

2. F=-(x-xip)/h;

 

vx.m

1. function F=vx(x,a0,a1,U1,Un)

2. F=U1+(Un-U1)/(a1-a0)*(x-a0);

 

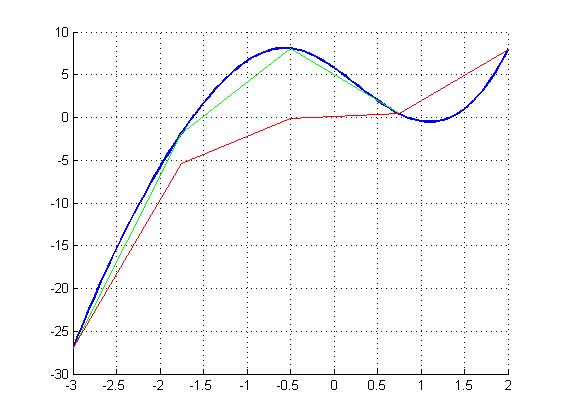
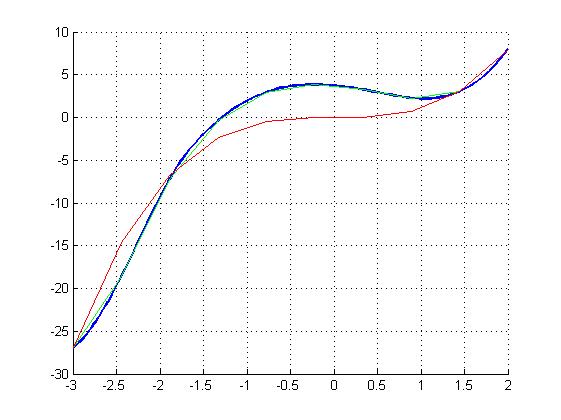
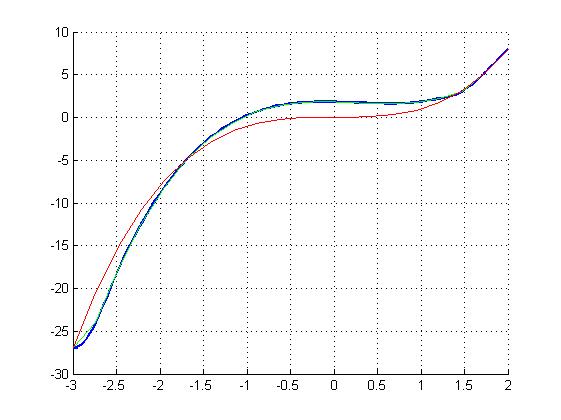
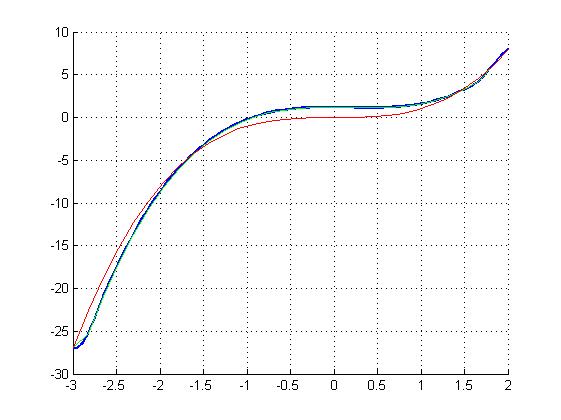
Результаты.

Легенда:

Точный график

График, полученные МКЭ.

Интерполяция кубическим сплайном графика, полученного МКЭ.

N=5

 

N=10

N=20

 

N=30

N=80

Вывод.

При увеличении количества разбиений результат МКЭ становится всё ближе к точному решению. Но при этом, задачи подобно разобранной, нет смысла решать, используя именно МКЭ, будет вполне достаточно и более простого в реализации МКР. МКЭ в основном используется для многомерных сложных задач. В них основным преимуществом МКЭ является возможность в случае необходимости выбрать более мелкое разбиение того участка, который в задаче интересует больше, значительно увеличивая скорость расчета для сложных систем.