Если булевы операции заменить обычными алгебраическими операциями, нахождение матрицы достижимости сведётся к обычному пошаговому перемножению матриц.

Построим матрицы смежности графа G (рисунок 5).

Рисунок 5 - Матрица смежности ||H|| графа G

Получим матрицу достижимости ||Q|| графа G (рисунок 6).

Рисунок 6 - Матрица достижимости ||Q|| графа G

H2

Возведем матрицу смежности ||H|| в квадрат, т.е. умножим ее саму на себя. Получим ||H²|| (рисунок 7).

Рисунок 7 - Матрица ||H²|| графа G

Возведем матрицу смежности ||H|| в третью степень. Получим ||H³|| (рисунок 8).

Рисунок 8 - Матрица ||H³|| графа G

Анализ матриц ||H²|| и ||H³|| показывает, что никаких изменений в ||H³|| по сравнению ||H²|| нет. Это значит, что процесс вычислений завершен.

Матрица достижимости ||Q³|| (рисунок.9) рассчитывается следующим образом:

Рисунок 5.9 - Матрица ||Q³|| графа G

Поскольку матрица ||Q³|| содержит два блока: один – 3х3 элемента, другой – 6х6 элементов, то граф G содержит два связных подграфа:

	G1=<X1, H1>, G2=<X2, H2>;,

где X₁={x₁,x₂,x₃}, X₂={x₄,x₅,x₆,x₇,x₈,x₉}.

Таким образом, для исходного графа G=<X,H>; число компонент связности равно æ(G)=2.

1. Расчет цикломатического числа λ(G) графа G

Рассчитаем цикломатическое число графа G, т.е. наименьшее число ребер, удаление которых приведет к графу без циклов и петель.

Расчет выполним по формуле:

	.

В качестве примера удалим на графе G четыре ребра (1,3), (4,5), (5,6), (8,9). Получим граф на рисунке 10.

Рисунок 10 - Граф без циклов и петель

1. Расчет хроматического числа γ(G) графа G

Рассчитаем хроматическое число графа G, т.е. наименьшее число красок при применении которых для раскраски вершин графа две любые смежные вершины графа G, не будут окрашены в один цвет.

Для выполнения расчета воспользуемся двумя оценочными соотношениями. Одно из них задает левую границу для γ(G), min возможное значение γ(G), т.е. γ_min(G):

1) полный n -вершинный граф имеет γ_min(G)=n;

2) пустой граф имеет γ_min(G)=1;

3) граф с циклом (т.е. хотя бы одним) четной длины имеет γ_min(G)=2;

4) граф с циклом нечетной длины имеет γ_min(G)=3;

5) граф-дерево имеет γ_min(G)=2.

Другое оценочное соотношение задает правую границу для γ(G), max необходимое значение γ(G), т.е. γ_max(G):

.

Начинаем проверку с вычисления γ_min(G). Поскольку в графе G есть цикл нечетной длины пробуем раскрасить граф тремя красками (рисунок 11).

Рисунок 11 - Раскраска графа G синей, желтой и красной красками

Вывод: трех красок, т.е. γ_min(G) =3 оказалось достаточно:

.

Если бы трех красок оказалось недостаточно, следовало бы γ_min(G) увеличить на единицу и повторить раскраску заново. И так далее, до получения желаемого результата. Однако таких красок не должно быть больше чем γ_max(G).
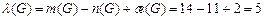
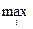