Необходимые и достаточные условия периодичности.
Рассмотрим систему:
Сначала мы не будем делать никаких предположений о природе коэффициентов Пусть
Для того чтобы это решение было периодическим с периодом
Очевидно, что условия (2.2) необходимы, так как функция называется периодической, если она удовлетворяет условиям:
каково бы не было
или
Так как это равенство справедливо для любых Предположим далее, что система фундаментальных решений системы:
нам известна. Обозначим эти функции через
где Подставим выражения (2.5) в (2.1). Принимая во внимание, что функции
откуда
где
Постоянные
Используя полученные выражения, выпишем теперь условия периодичности (2.2)
Для того чтобы система (2.1) допускала периодические решения, необходимо и достаточно, чтобы функции Рассмотрим эти условия для некоторых специальных случаев, так как это будет играть в дальнейшем изложении особую роль. Сначала рассмотрим тот частный случай, когда фундаментальные решения Так как C и D – постоянные числа, то в силу периодичности функции
Равенства (2.7’) позволяют упростить систему (2.8), которую можно теперь рассматривать как систему однородных алгебраических уравнений относительно интегралов
Перепишем эту систему в следующем виде:
Определитель системы (2.9) есть определитель Вронского для функций
Итак, мы пришли к следующему результату: если фундаментальное решение системы (2.4) выражается периодическими функциями, то для того, чтобы любое решение системы (2.1) было периодическим необходимо и достаточно, чтобы функции Сейчас рассмотрим тот частный случай, когда система (2.1) имеет вид
Система (2.11) сводится к уравнению колебаний математического маятника под действием периодической внешней силы
где
Линейно независимые решения системы (2.11) имеют вид
Определитель Вронского этих функций равен единице, поэтому условия (2.10) будут приведены к такому виду:
Раздел 3. Метод Ляпунова.
|

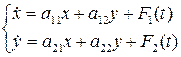 (2.1)
(2.1)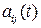 , кроме предположения об их периодичности по
, кроме предположения об их периодичности по 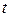 .
.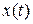 и
и 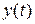 ─ решение системы (2.1), удовлетворяющее следующим данным Коши:
─ решение системы (2.1), удовлетворяющее следующим данным Коши: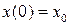 ,
,  .
.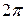 , необходимо и достаточно, чтобы оно удовлетворяющее следующим условиям:
, необходимо и достаточно, чтобы оно удовлетворяющее следующим условиям: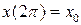 ,
, 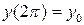 . (2.2)
. (2.2)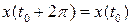 ,
, 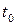 . Условия (2.2) являются частным случаем (2.3) при
. Условия (2.2) являются частным случаем (2.3) при 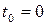 . Эти условия являются так же достаточными. В самом деле, правые части системы (2.1) ─ периодические функции времени периода
. Эти условия являются так же достаточными. В самом деле, правые части системы (2.1) ─ периодические функции времени периода 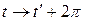 , тогда в силу (2.2) по
, тогда в силу (2.2) по 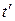 мы будем иметь одну и ту же задачу Коши и, следовательно,
мы будем иметь одну и ту же задачу Коши и, следовательно,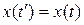 ;
; 
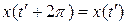 ;
;  .
. , то оно совпадает с (2.3) и, следовательно, функции
, то оно совпадает с (2.3) и, следовательно, функции 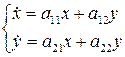 (2.4)
(2.4) ,
, 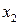 ,
,  и
и  , и решение системы (2.1) будем искать методом вариации произвольных постоянных, полагая
, и решение системы (2.1) будем искать методом вариации произвольных постоянных, полагая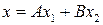 ,
,  . (2.5)
. (2.5)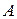 и
и 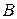 ─ некоторые функции времени, подлежащие определению.
─ некоторые функции времени, подлежащие определению. ,
, 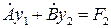 ,
,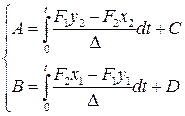 (2.6)
(2.6)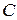 и
и 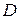 ─ новые произвольные постоянные, а
─ новые произвольные постоянные, а  ─ определитель Вронского
─ определитель Вронского
 .
.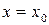 ,
, 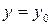 при
при  . Так как интегральные слагаемые в выражениях (2.6) при
. Так как интегральные слагаемые в выражениях (2.6) при  (2.7)
(2.7)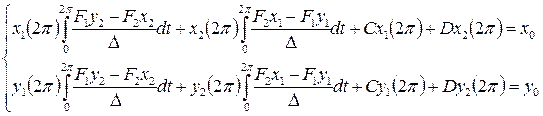 (2.8)
(2.8) и
и  удовлетворяли условиям (2.8).
удовлетворяли условиям (2.8).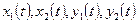 - периодические функции, Заметим, что уравнения в вариациях, отвечающие изохорным системам, т. е. системам, период колебаний которых не зависит от начальных условий, всегда имеют периодические решения.
- периодические функции, Заметим, что уравнения в вариациях, отвечающие изохорным системам, т. е. системам, период колебаний которых не зависит от начальных условий, всегда имеют периодические решения. и
и 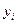 из (2.7), мы получаем следующие условия:
из (2.7), мы получаем следующие условия: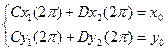 (2.7’)
(2.7’) .
.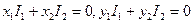 (2.9)
(2.9)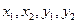 . В силу независимости этих функций он отличен от нуля. Таким образом, система (2.9) имеет только тривиальное решение. Поэтому
. В силу независимости этих функций он отличен от нуля. Таким образом, система (2.9) имеет только тривиальное решение. Поэтому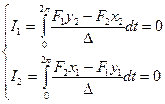 (2.10)
(2.10) и
и 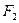 удовлетворяли условиям (2.10).
удовлетворяли условиям (2.10).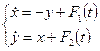 (2.11)
(2.11)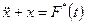

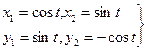 (2.12)
(2.12) (2.13)
(2.13)


