x(t) y(t)Контрольная работа № 1 По дисциплине «Автоматизация производственных процессов и производств» Тема: «Расчет динамических и частотных характеристик объекта» ВАРИАНТ № 32 Структурная схема объекта имеет вид: x(t) y(t)
Передаточные функции соединения равны соответственно:
Определить в общем и частном виде: 1. Дифференциальное уравнение соединения; 2. Передаточные функции для разомкнутой и замкнутой системы; 3. Записать характеристическое уравнение разомкнутой и замкнутой системы; 4. Выражения для временных характеристик разомкнутой системы. Построить графики h(t),w(t). 5. Выражения для частотных характеристик разомкнутой системы. Построить графики A(w),j(w),W(jw). 6. Дифференциальное уравнение для замкнутой системы.
Объект представляет собой последовательное соединение идеального дифференцирующего звена с передаточной функцией Последовательным называется соединение двух или нескольких звеньев, при котором сигнал на выходе предыдущего звена является входным для последующего.
Идеальное дифференцирующее звено описывается уравнением:
Апериодическое звено 1-го порядка описывается дифференциальным уравнением: передаточной функцией: где к- коэффициент передачи, Т- постоянная времени звена,с.
Передаточной функцией звена (системы) называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при условии, что все остальные воздействия равны нулю.
Передаточная функция разомкнутой системы по задающему воздействию находится путём перемножения передаточных функций всех звеньев прямой цепи регулирования.
Передаточная функция замкнутой системы находится из выражения:
где W(p)- передаточная функция разомкнутой системы, M(p),N(p),D(p)- полиномы от комплексной переменной р.
Так как соединение последовательное, то передаточную функцию разомкнутой системы получим как произведение передаточных функций звеньев:
Подставим в (1) значения параметров объекта и получим выражение для передаточной функции разомкнутой системы в частном виде:
Передаточную функцию замкнутой системы найдем по формуле:
Подставим в (2) параметры объекта, получим передаточную функцию замкнутой системы в частном виде:
Характеристическим уравнением разомкнутой (замкнутой) системы называется полином знаменателя передаточной функции разомкнутой (замкнутой) системы, приравненный нулю (N(p)=0, D(p)=0).
Согласно определению, характеристическое уравнение разомкнутой системы найдем из выражения (1):
и в частном виде:
Характеристическое уравнение замкнутой системы:
и в частном виде:
Дифференциальное уравнение соединения найдем из передаточной функции разомкнутой системы (1):
Последнее выражение есть дифференциальное уравнение соединения в общем виде. В частном виде, получим следующее выражение:
Найдем временные характеристики соединения:
Переходной характеристикой h(t) звена (системы) называется его реакция на воздействие в виде единичной ступенчатой функции при нулевых начальных условиях. Весовой функцией звена (системы) называется его реакция на воздействие в виде единичной импульсной функции при нулевых начальных условиях.
Переходная функция:
В частном виде:
Весовая функция:
В частном виде:
По выражениям (3), (4) строим графики переходной и весовой функций.
Рис.1 а) Переходная б) весовая функция функция
Амплитудно – частотной характеристикой (АЧХ) A(w) называется зависимость отношения амплитуды выходного сигнала
Фазо-частотной характеристикой (ФЧХ) называется зависимость сдвига по фазе выходного сигнала относительно входного от частоты w.
Амплитудно-фазовая характеристика АФХ отражает как свойство изменять амплитуду выходного сигнала, так и свойство задерживать сигнал на каждой частоте на определенную величину j.
Выражение для построения АФХ получают из передаточной функции W(p) заменой комплексной переменной р на jw. Так как W(jw) комплексная функция, то её можно представить в алгебраической и показательной форме записи. Алгебраическая форма записи:
Здесь U(w)-вещественная частотная характеристика (ВЧХ); V(w)-мнимая частотная характеристика (МЧХ).
Найдем частотные характеристики соединения:
Комплексная частотная характеристика:
Найдем вещественную (ВЧХ) и мнимую (МЧХ) частотные характеристики, умножив числитель и знаменатель выражения (5) на комплексно-сопряженное знаменателя:
Отсюда
По выражению (6) строим амплитудно-фазовую характеристику (рис.2.в) Найдем выражения для амплитудно-частотной (АЧХ) и фазо-частотной характеристик (ФЧХ) соединения как модуль и аргумент комплексной частотной передаточной функции соответственно. Амплитудно-частотная характеристика имеет вид:
Фазо-частотная характеристика имеет вид:
По выражениям (7),(8) строим АЧХ и ФЧХ (рис.2 а,б):
Рис.2 а) АЧХ б)ФЧХ в) АФХ
Из выражения (2) получим дифференциальное уравнение замкнутой системы:
|

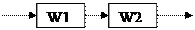

 и апериодического звена 1-го порядка с передаточной функцией
и апериодического звена 1-го порядка с передаточной функцией  .
.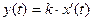
 ;
; ,
, ,
,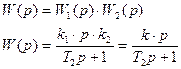 (1)
(1)
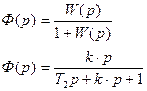 (2)
(2)
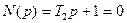


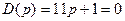

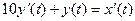
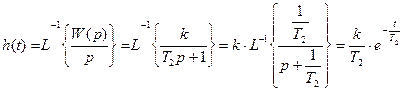
 (3)
(3)
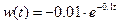 (4)
(4)
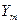 к амплитуде входного сигнала
к амплитуде входного сигнала 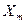 от частоты w.
от частоты w.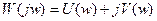
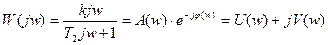
 (5)
(5)
 (6)
(6) (7)
(7) (8)
(8)




