Устойчивость цифровых систем управления.3.3.1. Варианты оценки устойчивости. Первый вариант. Устойчивость цифровой системы управления оценивается по показателям цифровой системы управления. Второй вариант. Устойчивость цифровой системы управления оценивается по показателям устойчивости непрерывных систем управления, с использованием для этого непрерывного эквивалента цифровой системы управления. В дальнейшем приводятся показатели устойчивости цифрового варианта системы управления, полагая, что показатели устойчивости непрерывных систем управления известны.
3.3.2. Общее условие устойчивости цифровой системы управления. Необходимым и достаточным условием устойчивости цифровой системы управления является условие, состоящее в том, чтобы все корни характеристического уравнения по модулю были бы меньше единицы. Если имеется хотя бы один корень характеристического уравнения по модулю равный единице, а все остальные корни по модулю меньше единицы цифровая система управления находится на границе устойчивости. Характеристическое уравнение соответствующей системы управления может быть получено: 1) 2) Приравниванием знаменателя соответствующей передаточной функции нулю.
3.3.3. Алгебраический критерий устойчивости Джури. Для цифровых систем управления, также как и для непрерывных систем управления, в основе алгебраических критериев устойчивости лежит процедура составления определенных соотношений из коэффициентов характеристического уравнения и оценки по этим соотношениям устойчивости системы управления. Рассмотрим сначала необходимое условие устойчивости. Пусть характеристическое уравнение имеет следующий вид:
Для того, чтобы корни этого уравнения были меньше единицы
Доказать это просто. Допустим, что корни характеристического уравнения найдены, тогда характеристическое уравнение можно представить в виде:
Очевидно, что если все корни
Тот же результат получим и в другом неравенстве
Так как все скобки отрицательны. Пример.
Необходимое условие устойчивости не выполняется, следовательно, система не устойчива.
Сущность алгебраического критерия устойчивости Джури поясняется на примере цифровой системы управления 4-го порядка. Для оценки устойчивости составляется таблица Джури. Она содержит (n+1) строк и столько же столбцов. Заполненная таблица имеет вид треугольника. Пусть имеем характеристическое уравнение четвертого порядка.
Нулевая строка таблицы Джури состоит из коэффициентов характеристического уравнения, а под ней располагается строка состоящая из тех же коэффициентов, но записанных в обратном порядке. 1. Определяем коэффициент Вычисляем коэффициенты первой строки:
Обращаем внимание на то, что коэффициент Запишем коэффициенты первой строки таблицы Джури, состоящей из коэффициентов 2. Определяем коэффициент Вычисляем коэффициенты второй строки:
Коэффициент Запишем коэффициенты второй строки таблицы Джури, состоящей из коэффициентов 3. Определяем коэффициент Вычисляем коэффициенты третьей строки:
Коэффициент Запишем коэффициенты третьей строки таблицы Джури, состоящей из коэффициентов 4. Определяем коэффициент Вычисляем единственный коэффициент последней, четвертой строки:
Коэффициент После проведенных вычислений можно составить таблицу Джури:
Определение критерия Джури. Для устойчивости дискретной системы необходимо и достаточно, чтобы все элементы нулевого столбца Замечание. Положительность последнего нулевого элемента в таблице Джури следует автоматически при выполнении необходимого условия устойчивости.
3.3.4. Аналог частотного критерия устойчивости Михайлова. Характеристический полином цифровой системы управления имеет вид:
Характеристический полином Михайлова (вектор Михайлова) получается путем перехода из операторной области в частотную заменив
Графическое представление характеристического полинома Михайлова (годограф Михайлова) имеет периодический характер. Формулировка критерия: необходимым и достаточным условием устойчивости цифровой системы управления является условие состоящее в том, чтобы изменение аргумента вектора Михайлова при изменении частоты от 0 до
Процедура оценки устойчивости цифровой системы управления по аналогу критерия устойчивости Михайлова: 1) в соответствии с порядком характеристического полинома определить требуемое изменение аргумента вектора Михайлова
2) построить годограф Михайлова 3) по годографу Михайлова определить действительное изменение вектора Михайлова
4) цифровая система управления устойчива, если действительное изменение аргумента вектора Михайлова равно требуемому, т.е.
3.3.5.Аналог частотного критерия устойчивости Найквиста. Частотный критерий устойчивости Найквиста позволяет по амплитудно-фазовой частотной характеристике разомкнутой системы управления оценивать устойчивость замкнутой системы управления. Особенности характеристик разомкнутой системы управления: 1) амплитудно-фазовая частотная характеристика разомкнутой системы управления является периодической функцией частоты 2) разомкнутая система устойчива, если все корни характеристического уравнения по модулю меньше единицы (т.е. находятся внутри единичного круга); 3) разомкнутая система управления неустойчива, если имеется хотя бы один корень по модулю больший единицы. Вектор Найквиста – вектор, проведенный из критической точки (-1,0) в соответствующую точку амплитудно-фазовой частотной характеристики разомкнутой системы. Вектор Найквиста определяется соотношением
Формулировка критерия: если разомкнутая система неустойчива, имеет r – корней по модулю больших единицы (r-корней вне единичного круга), то необходимым и достаточным условием устойчивости замкнутой цифровой системы управления является условие состоящее в том, чтобы изменение аргумента вектора Найквиста при изменении частоты от 0 до Процедура оценки устойчивости цифровой системы управления по критерию Найквиста: 1) в соответствии с состоянием разомкнутой системы определить требуемое изменение аргумента вектора Найквиста
2) построить амплитудно-фазовую частотную характеристику разомкнутой системы
3) по амплитудно-фазовой частотной характеристике определить действительное изменение аргумента вектора Найквиста
4) замкнутая цифровая система управления устойчива, если действительное изменение аргумента вектора Найквиста равно требуемому:
3.3.6.Оценка устойчивости цифровой системы управления по ее непрерывному эквиваленту. Для оценки устойчивости цифровой системы управления по ее непрерывному эквиваленту необходимо, воспользовавшись соотношением между операторами 3.3.7. Области устойчивости. Области устойчивости представляют совокупность параметров системы управления, при которых система управления устойчива. При построении области устойчивости координатами являются параметры, влияние которых на устойчивость рассматривается. Особенностью цифровых систем управления является то, что на устойчивость системы управления кроме таких параметров системы как коэффициенты усиления, постоянные времени влияет также период дискретности, по сути являющийся параметром системы управления. В том случае, если рассматривается один параметр системы управления, то определяется его предельное значение. Процедура построения области устойчивости цифровой системы управления: 1) выбрать критерий устойчивости системы управления; 2) записать условие устойчивости системы управления (неравенство); 3) записать уравнение для границы устойчивости (равенство); 4) построить границу устойчивости в выбранной системе координат; 5) используя условие устойчивости, определить область устойчивости.
3.3.8.Задачи. Раздел А. Задано: разностное уравнение разомкнутой системы управления (см.п.3.2.8.). Оценить устойчивость разомкнутой и замкнутой систем управления при следующих значениях коэффициентов разностного уравнения, используя различные критерии устойчивости.
Для вариантов 1-6,8 определить критическое значение коэффициента Раздел Б. Задана передаточная функция разомкнутой системы управления 1) 2) Оценить устойчивость разомкнутой и замкнутой систем управления. Раздел В. Задана передаточная функция замкнутой системы: 1) 4) Оценить устойчивость цифровой системы управления. Раздел Г. Задана передаточная функция замкнутой системы управления: 1) 3) 5) Определить из условия устойчивости предельное значение периода дискретности. Раздел Д. Задано: - передаточная функция объекта управления - устройство связи с объектом управления: фиксирующее звено нулевого порядка; - передаточная функция регулятора Построить области устойчивости в системах координат
|

 -изображением левой части разностного уравнения n-го порядка и приравниванием этого изображения нулю. Общий вид характеристического уравнения имеет вид
-изображением левой части разностного уравнения n-го порядка и приравниванием этого изображения нулю. Общий вид характеристического уравнения имеет вид 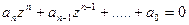 по прямой разности и
по прямой разности и  по обратной разности.
по обратной разности.
 , необходимо чтобы при
, необходимо чтобы при 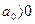 , выполнялись неравенства:
, выполнялись неравенства: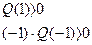
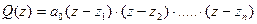
 , то при
, то при 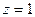
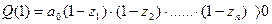
 . Так, например, если n=3, то:
. Так, например, если n=3, то: ,
,
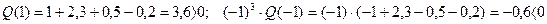 .
.
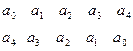

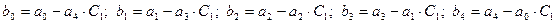
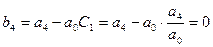
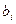 , а под ней те же коэффициенты, но в обратном порядке
, а под ней те же коэффициенты, но в обратном порядке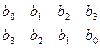
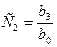 .
.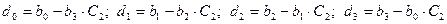
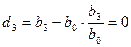
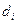 , а под ней те же коэффициенты, но в обратном порядке:
, а под ней те же коэффициенты, но в обратном порядке: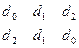


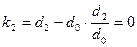
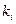 , а под ней те же коэффициенты, но в обратном порядке:
, а под ней те же коэффициенты, но в обратном порядке:
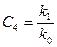

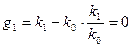

 были положительны.
были положительны.

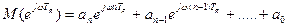
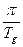 было бы равно
было бы равно  .
.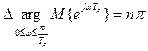


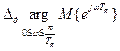
 ;
;
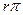 .
.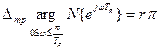
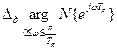
 .
.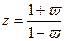 , получить математическую модель системы в непрерывной форме эквивалентную математической модели цифровой системы управления. После этого использовать полученную математическую модель для оценки устойчивости цифровой системы управления методами оценки устойчивости непрерывных систем управления.
, получить математическую модель системы в непрерывной форме эквивалентную математической модели цифровой системы управления. После этого использовать полученную математическую модель для оценки устойчивости цифровой системы управления методами оценки устойчивости непрерывных систем управления.

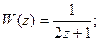 2)
2) 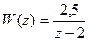 ; 3)
; 3) 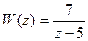 ; 4)
; 4)  ;
;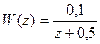 .
. ;2)
;2) 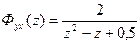 ;3)
;3) 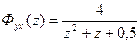 ;
; .
.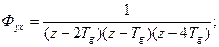 2)
2) 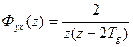 ;
; ; 4)
; 4) 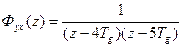 ;
; ; 6)
; 6) 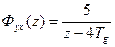 .
.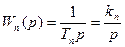 ;
;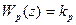 .
.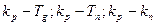 .
.


