По закону Ома ток линии 4 страница
Определить и записать в табл. 6.3 активную P п и реактивную Q п мощности приемника при напряжении на его зажимах U 2, а также мощность батареи конденсаторов QС = P (tgjп–tgj2), необходимую для получения заданного вариантом коэффициента реактивной мощности tgj2 (табл. 6.1). Таблица 6.1
Порядок выполнения эксперимента 1. Собрать электрическую цепь по схеме рис. 6.2
2. Установить на зажимах потребителя напряжение U 2 согласно варианту табл. 6.1 и поддерживать его неизменным при всех измерениях. Изменяя емкость С батареи конденсаторов от нуля до наибольшего значения, измерить величины, указанные в табл. 6.2. Таблица 6.2
3. Выполнить экспериментальную проверку предварительного задания. По результатам измерений при IC = 0 (табл. 6.2) рассчитать и записать в табл. 6.3 экспериментальные данные приемника Z п, jп, tgjп, P п, Q п. Изменяя емкость батареи конденсаторов, довести коэффициент реактивной мощности tgj2 до значения, заданного в табл. 6.1. Определить мощность QC = U 2 IC и сравнить ее с найденной в предварительном расчете (табл. 6.3). Таблица 6.3
4. На основании данных табл. 6.2 вычислить и записать в табл. 6.4 активную мощность в конце линии P 2 = U 2 I л cosj2, активную мощность в начале линии P 1 = U 1 I л cosj1, потери мощности DР, КПД h, потерю напряжения DU, реактивную мощность в конце линии Q 2 = U 2 I л sinj2, мощность батареи конденсаторов QC, емкость батареи конденсаторов С. Таблица 6.4
5. Построить совмещенные графики зависимостей I Л, D U, D Р, h, Q 2, где Q п – реактивная мощность потребителя, равная значению Q 2 при QC = 0;
На основании данных табл. 6.2 построить в масштабе векторные диаграммы напряжений и токов для трех опытов: двух крайних и одного промежуточного. Содержание отчета 1. Цель работы. 2. Расчет предварительного задания. 3. Схема исследованной электрической цепи. 4. Таблицы измерений и вычислений. 5. Графики зависимостей. 6. Три векторные диаграммы. 7. Выводы о влиянии компенсации реактивной мощности на технико-экономические показатели электропередачи. Контрольные вопросы 1. Дайте определение коэффициента реактивной мощности? 2. Какие отрицательные последствия вызывает передача потребителю реактивной мощности из энергосистемы? 3. Назовите организационно-технические мероприятия, снижающие потребление реактивной мощности. 4. Как осуществляется компенсация реактивной мощности? 5. Какова целесообразная степень компенсации реактивной мощности? 6. В чем состоит физическая сущность компенсации реактивной мощности с помощью батареи конденсаторов? Лабораторная работа 1.7 ТРЕХФАЗНЫЕ ЦЕПИ Цель работы: исследование режимов работы четырех– и трехпроводных трехфазных цепей при соединении приемников звездой и треугольником. Общие сведения Трехфазной называют совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты и амплитуды, но сдвинутые по фазе одна относительно другой на угол 120°. Одним из преимуществ трехфазных цепей является возможность получения в одной электротехнической установке двух эксплуатационных напряжений – фазного и линейного, отличающихся друг от друга в Приемники соединяются звездой в том случае, когда их номинальное напряжение равно фазному напряжению источника. При соединении приемников по схеме звезды концы трех фаз X, Y, Z объединяются в одну общую точку n, называемую нейтральной. Нейтральная точка N источника питания может быть соединена с нейтральной точкой n приемника. Провод, соединяющий нейтральные точки N и n, называется нейтральным, а трехфазная цепь – четырехпроводной. Она применяется для питания несимметричных приемников (
Из схемы (рис. 7.1 а) видно, что при соединении приемников звездой фазные токи равны соответствующим линейным токам: I ф = I л. По первому закону Кирхгофа ток нейтрального провода равен геометрической сумме фазных токов:
Линейные напряжения определяются геометрической разностью соответствующих фазных напряжений
При наличии нейтрального провода Токи в каждой фазе приемника определяются по формулам:
Векторная диаграмма напряжений и токов изображена на рис. 7.2а.
При симметричной нагрузке ( При несимметричной нагрузке в трехфазной трехпроводной цепи между нейтральными точками приемника n и источника N появляется напряжение
где
Фазные напряжения приемников находят на основании второго закона Кирхгофа:
Токи определяют по закону Ома
По схеме треугольника соединяются приемники, номинальные напряжения которых равно линейному напряжению источника. В этой схеме конец предыдущей фазы соединяется в одну точку с началом следующей (рис. 7.1 б) и каждая фаза приемника оказывается включенной на линейное напряжение источника, т.е. фазные напряжения приемника равны соответствующим линейным напряжениям источника питания: U ф = U л . Так как линейные напряжения источника практически не изменяются, то каждая фаза приемника работает независимо друг от друга, и треугольником соединяют как симметричную, так и несимметричную нагрузки. Записав фазные напряжения приемника в комплексной форме
фазные токи определяют по закону Ома:
Линейные токи определяют как геометрическую разность соответствующих фазных токов из уравнений, составленных согласно первому закону Кирхгофа для узлов a, b и c (рис. 7.1б):
Векторная диаграмма напряжений и токов для нагрузки, соединенной треугольником, изображена на рис. 7.3.
При симметричной нагрузке (
Предварительное задание к эксперименту 1. Начертить схему четырехпроводной трехфазной цепи (сопротивления приемников заданы в табл. 7.1). 2. Записать в комплексной форме фазные напряжения трехфазной цепи, если линейное напряжение U л = 220 В. Рассчитать в четырехпроводной трехфазной цепи фазные токи приемников и ток в нейтральном проводе. Результаты расчета записать в табл. 7.2. Для проверки результатов расчета воспользоваться ПЭВМ, программа «cepi exe». 3. Начертить схему трехфазной цепи при соединении заданных в табл. 7.1 приемников треугольником. Записать в комплексной форме линейные напряжения и рассчитать фазные и линейные токи трехфазной цепи. Результаты расчета проверить на ПЭВМ (программа «cepi exe») и записать в табл. 7.3. 4. По результатам расчетов пунктов 2 и 3 построить векторные диаграммы напряжений и токов для каждой цепи. Таблица 7.1
Порядок выполнения эксперимента 1.Собрать четырехпроводную трехфазную цепь, используя приемники 2. Включить цепь под напряжение и измерить фазные (линейные) токи и напряжения приемников, ток IN, напряжение UnN. Результаты измерений записать в табл. 7.2. Сравнить их с результатами расчета. 3. Отключить нейтральный провод и провести исследование режима трехпроводной цепи согласно пункту 2. Сделать вывод о роли нейтрального провода. 4. В трехпроводной цепи выполнить опыты холостого хода фазы А ( 5. По результатам измерений пункта 4 построить две векторные диаграммы напряжений и токов (при Таблица 7.2
6. Собрать трехфазную цепь при соединении приемников 7. Включить цепь под напряжение и измерить фазные и линейные токи и напряжения. Результаты измерений записать в табл. 7.3. Сравнить их с результатами расчета. Таблица 7.3
Содержание отчета 1. Цель работы. 2. Схемы четырехпроводной и трехпроводной трехфазных цепей. Полный расчет заданного в предварительном задании режима работы этих цепей. 3. Таблицы вычислений и измерений. 4. Векторные диаграммы (две по результатам расчета и две по экспериментальным данным). 5. Сравнительный анализ изученных трехфазных цепей. Контрольные вопросы 1. Каковы преимущества и недостатки трехпроводных и четырехпроводных цепей. 2. Каково соотношение между линейными и фазными напряжениями и токами в четырехпроводной цепи? При каком условии эти соотношения сохраняются в трехпроводной цепи при соединении приемников звездой? 3. Каково назначение нейтрального провода в четырехпроводной цепи? 4. Когда приемники соединяются звездой, треугольником? 5. Что такое напряжение смещения нейтрали, когда оно появляется и как его определить? 6. Что происходит в трехпроводной симметричной цепи при обрыве и коротком замыкании одной из фаз? Пояснить с помощью векторных диаграмм. 7. Каковы соотношения между фазными и линейными напряжениями и токами при соединении симметричного приемника треугольником? 8. Как строятся векторные диаграммы напряжений и токов для исследованных цепей? 9. Как изменится мощность приемника при переключении его фаз со звезды на треугольник? Лабораторная работа 1.8 ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ РАЗРЯДЕ Цель работы:1) изучение влияния параметров разрядной цепи на процесс разряда конденсатора; 2) приобретение навыков применения электронного осциллографа для исследования переходных процессов. Общие сведения Процессы, происходящие при изменении режима электрической цепи, называют переходными. Они возникают в цепях, содержащих индуктивные и емкостные элементы, и обусловлены тем, что энергия магнитного и электрического полей не изменяется мгновенно. Расчет токов и напряжений переходного режима производят с помощью уравнений, составленных по законам Кирхгофа для мгновенных значений токов и напряжений. В электрической цепи с постоянными параметрами R, L, C эти уравнения представляют собой линейные дифференциальные уравнения с постоянными коэффициентами. Общее решение линейного дифференциального уравнения равно сумме частного решения данного уравнения и общего решения его (при равенстве нулю правой части). Частное решение находят для установившегося режима, полученные при этом токи и напряжения называют принужденными( Токи и напряжения, полученные в результате общего решения уравнения без правой части, называют свободными( 1. Ток в ветви с индуктивностью не изменяется скачком. 2. Напряжение на емкостном элементе не изменяется скачком. Алгебраическая сумма принужденной и свободной составляющих дает ток или напряжение переходного режима
Рассмотрим переходный процесс при разряде конденсатора, заряженного до напряжения U 0, через резистор с сопротивлением R (рис. 8.1а).
По второму закону Кирхгофа для цепи после коммутации
Так как Принужденная составляющая отсутствует, поэтому
где
Постоянную интегрирования А находим из начальных условий: при Выражения для напряжения на конденсаторе при его разряде и тока разряда (рис. 8.1 б) имеют вид
В процессе разряда конденсатора вся энергия его электрического поля превращается в тепло в резисторе R
При подключении заряженного конденсатора к катушке с активным сопротивлением R и индуктивностью L (рис. 8.2а) в зависимости от соотношения параметров R, L, C возможен апериодический или периодический (колебательный) разряд конденсатора. В случае апериодического разряда напряжение на конденсаторе uc и ток i изменяются только по величине, не изменяя направления. С энергетической точки зрения это означает, что запасенная в конденсаторе энергия электрического поля
Процессы, возникающие в контуре (рис. 8.2а), описываются следующим дифференциальным уравнением:
Принужденный режим в цепи отсутствует и
которому соответствует характеристическое уравнение
Решение уравнения (8.2), т.е. характер разряда конденсатора, зависит от вида корней характеристического уравнения
которые могут быть действительными разными, действительными равными и комплексными сопряженными. Апериодический разряд имеет место, если корни действительные и различные, т.е.
В этом случае напряжение и ток
Кривые изменения напряжения на емкости и тока контура приведены на рис. 8.2б. Предельный случай апериодического разряда – критический разряд – имеет место, если
R кр – критическое сопротивление – такое наименьшее сопротивление контура, при котором процесс разряда еще имеет апериодический характер. Колебательный разряд конденсатора будет при условии, если
Корни в этом случае комплексные и сопряженные
где
цепи R, L, C;
Выражения напряжения uc и тока i при колебательном разряде конденсатора
|


 – степень компенсации реактивной мощности.
– степень компенсации реактивной мощности.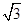 раз. Это позволяет применять две схемы соединения трехфазных приемников: звезда(рис. 7.1 а) и треугольник(рис. 7.1 б).
раз. Это позволяет применять две схемы соединения трехфазных приемников: звезда(рис. 7.1 а) и треугольник(рис. 7.1 б).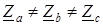 ). Нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Благодаря ему, изменение нагрузки в любой из фаз приемника приводит к изменению токов только в данной фазе и в нейтральном проводе, а в других фазах режим работы не меняется.
). Нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Благодаря ему, изменение нагрузки в любой из фаз приемника приводит к изменению токов только в данной фазе и в нейтральном проводе, а в других фазах режим работы не меняется.
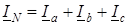

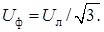
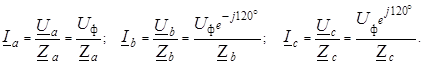

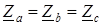 ) токи равны по величине и сдвинуты по фазе на угол 120° друг относительно друга. Ток в нейтральном проводе отсутствует (IN = 0), и необходимость в этом проводе отпадает. Трехфазная цепь в этом случае выполняется трехпроводной (без нейтрального провода). Следовательно, в трехпроводную цепь при соединении нагрузки «звездой» включаются только симметричные трехфазные приемники: электрические двигатели, электрические печи и др.
) токи равны по величине и сдвинуты по фазе на угол 120° друг относительно друга. Ток в нейтральном проводе отсутствует (IN = 0), и необходимость в этом проводе отпадает. Трехфазная цепь в этом случае выполняется трехпроводной (без нейтрального провода). Следовательно, в трехпроводную цепь при соединении нагрузки «звездой» включаются только симметричные трехфазные приемники: электрические двигатели, электрические печи и др.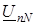 , называемое напряжением относительно нейтрали или напряжением смещения нейтрали (рис.7.2 б). Напряжение смещения нейтрали рассчитывается по методу двух узлов:
, называемое напряжением относительно нейтрали или напряжением смещения нейтрали (рис.7.2 б). Напряжение смещения нейтрали рассчитывается по методу двух узлов:
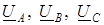 – фазные напряжения источника,
– фазные напряжения источника,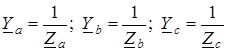 – комплексные проводимости фаз приемника.
– комплексные проводимости фаз приемника.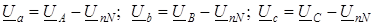 .
.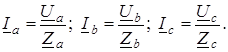
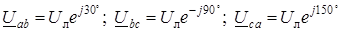 ,
,
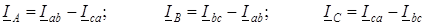

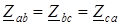 ) фазные токи равны по величине, а углы сдвига фаз токов по отношению к соответствующим напряжениям одинаковы (j ab = j bc = j ca). Линейные токи будут в
) фазные токи равны по величине, а углы сдвига фаз токов по отношению к соответствующим напряжениям одинаковы (j ab = j bc = j ca). Линейные токи будут в 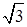 раз больше фазных токов.
раз больше фазных токов.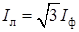
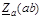 , Ом
, Ом
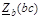 , Ом
, Ом
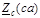 , Ом
, Ом
 согласно табл. 7.1. Включить амперметры для измерения фазных токов и тока нейтрального провода.
согласно табл. 7.1. Включить амперметры для измерения фазных токов и тока нейтрального провода.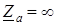 ) и короткого замыкания (
) и короткого замыкания (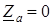 ). Измерить и записать в табл. 7.2 напряжения и токи в этих режимах.
). Измерить и записать в табл. 7.2 напряжения и токи в этих режимах.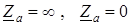 ).
). Вычислено
Вычислено
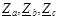 (табл.7.1)
(табл.7.1)
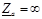
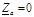
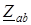 ,
,  ,
, 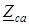 (табл. 7.1) треугольником.
(табл. 7.1) треугольником.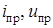 ).
). ). Постоянные интегрирования уравнений для свободных составляющих определяют из начальных условий, используя два закона коммутации:
). Постоянные интегрирования уравнений для свободных составляющих определяют из начальных условий, используя два закона коммутации: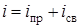 ;
;  .
.
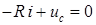 .
.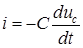 , то
, то 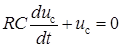 .
.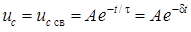 ,
,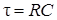 – постоянная времени – это время, за которое свободная составляющая уменьшается в e =2,718 раз;
– постоянная времени – это время, за которое свободная составляющая уменьшается в e =2,718 раз;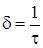 – коэффициент затухания.
– коэффициент затухания.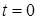
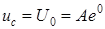 , т.е.
, т.е. 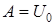 .
.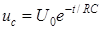 ;
; 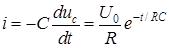 .
.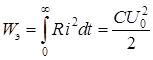 .
.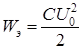 преимущественно поглощается в сопротивлении R и лишь небольшая часть переходит в энергию магнитного поля катушки
преимущественно поглощается в сопротивлении R и лишь небольшая часть переходит в энергию магнитного поля катушки 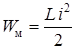 . Начиная с некоторого момента времени, в тепло преобразуется не только оставшаяся энергия электрического поля конденсатора, но и энергия, запасенная в магнитном поле катушки.
. Начиная с некоторого момента времени, в тепло преобразуется не только оставшаяся энергия электрического поля конденсатора, но и энергия, запасенная в магнитном поле катушки. При колебательном разряде напряжение u cи ток i изменяются как по величине, так и по направлению. Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного поля и обратно, причем эти колебания сопровождаются потерей энергии в активном сопротивлении. В процессе колебаний первоначально запасенная энергия
При колебательном разряде напряжение u cи ток i изменяются как по величине, так и по направлению. Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного поля и обратно, причем эти колебания сопровождаются потерей энергии в активном сопротивлении. В процессе колебаний первоначально запасенная энергия 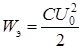 постепенно преобразуется в тепло в активном сопротивлении и рассеивается в окружающем пространстве.
постепенно преобразуется в тепло в активном сопротивлении и рассеивается в окружающем пространстве.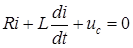 . (8.1)
. (8.1) ;
; 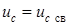 . Подставляя значение
. Подставляя значение 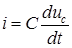 в уравнение (8.1), после дифференцирования получаем дифференциальное уравнение второго порядка
в уравнение (8.1), после дифференцирования получаем дифференциальное уравнение второго порядка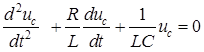 , (8.2)
, (8.2)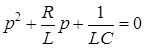 .
.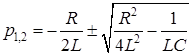 ,
,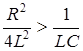 или
или  .
. ;
;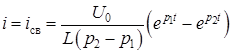 .
.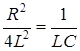 или
или 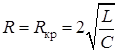 ;
;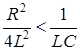 или
или 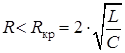 .
.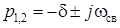 ,
,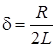 – коэффициент затухания;
– коэффициент затухания; – угловая частота свободных колебаний
– угловая частота свободных колебаний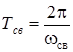 – период свободных колебаний.
– период свободных колебаний.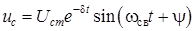 ;
; .
.


