Просторові кристалічні ґратки. Ґратки Браве.
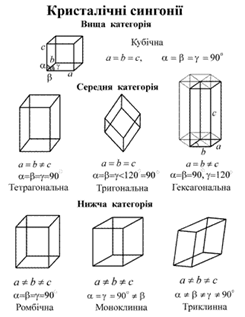
Спочатку введемо поняття про особливі напрямки у кристалі. Єдиний, той що не повторюється, напрямок у кристалі, називається особливим, або одиничним. В залежності від кількості особливих напрямків і кількості осей симетрії кристали поділяються на три категорії. Вища категорія. Немає особливих напрямків, є кілька (не менше двох) осей симетрії порядку вище, ніж 2. Це високосиметричні кристали. Будь-якому напрямку у них відповідають інші, які є симетрично еквівалентними. Анізотропія фізичних властивостей, таких як електропровідність, теплопровідність, діелектрична проникність, у таких кристалах відсутня. Середня категорія. Має один особливий напрямок, який співпадає із єдиною віссю симетрії порядку вище 2, тобто 3, 4 або 6. Це може бути трьох-, Нижча категорія. Має кілька особливих напрямків і не має осей порядку вище другого. Прикладом такого кристалу є так звана ромбічна призма. Якщо наочніше, це цеглина або сірникова коробка. Це найменш симетричні кристали із найбільшою анізотропією властивостей.
- 3 осі обертання 4 порядку; - 4 осі обертання 3 порядку; - 6 осей обертання 2 порядку; - 9 дзеркальних площин; - центр інверсії. Як бачимо, два різних кристали мають однаковий набір елементів симетрії
Отже, до вищої категорії відноситься лише одна сингонія – кубічна. Це єдина сингонія, симетрії якої відповідає звичайна декартова система координат
Її елементарна комірка – куб. Вона має 4 осі обертання 3 порядку. Це найхарактерніша ознака кубічного кристалу. До середньої категорії відносяться три сингонії. Тетрагональна (від грецьких слів “тетра” - чотири і “гоніо” – кут). Якщо взяти куб за протилежні грані і розтягти, отримаємо пряму призму із квадратною основою і висотою, яка не співпадає за розміром із стороною квадрату. Це і буде елементарна комірка тетрагональної системи. Співвідношення між сторонами і кутами для неї Вона має особливий напрямок вздовж висоти призми, і єдину вісь симетрії порядку вище 2, а саме 4 порядку. Тригональна (від грецьких слів “три” і “гоніо” – кут) (або ромбоедрична) точкова група відображає симетрію об’єкта, який утворюється, якщо розтягти куб вздовж об’ємної діагоналі. Ця діагональ є особливим напрямком і віссю обертання 3 порядку. Елементарна комірка утворюється трьома векторами однакової довжини, які утворюють між собою рівні кути. Гексагональна (з грецької “гекса” – шість). В гексагональній системі у якості елементарної комірки зручно вибрати пряму призму, в основі якої лежить ромб з кутами 60° і 120°. Її можна отримати із тетрагональної комірки, розтягши її за дві протилежні бічні сторони. Розміри і кути комірки ось такі Щоб підкреслити, що ця комірка належить до гексагональної сингонії, до неї додають ще дві, повернуті на кут 120°. Разом вони утворюють потрійну комірку у формі гексагональної призми. Особливий напрямок перпендикулярний основам призми і є віссю симетрії 6 порядку. І, нарешті, до нижчої категорії відносяться: Ромбічна. Якщо взяти тетрагональну структуру і Моноклінна. Назва походить від грецьких слів “моно” і “кліно”, тобто “один” і “нахилений”. Якщо натиснути на ромбічну гратку так, щоб дві протилежні бічні грані залишились прямокутниками, а решта перетворились на довільні паралелограми, отримаємо моноклінну структуру. У неї всі грані різні, два прямих кути і один від них відрізняється Триклінна. Назва від грецьких слів “три” і “кліно”, тобто “тричі нахилена”. Кристал із такою симетрією не має ні осей обертання, ні площин симетрії. В елементарній комірці всі розміри і кути різні Це сингонія з найменшою симетрією. Вона має лише центр інверсії. Таким чином, число точкових груп симетрії дорівнює семи. Кількість просторових груп симетрії, звичайно, більше, ніж кількість їх точкових груп, тому що в просторові групи додаються трансляції. Виявляється, що тільки 14 тривимірних точкових структур можуть мати трансляційну симетрію. Цікаво, що питання про число просторових ґраток у 1842 р. розглядав Франкгейм і помилився. Його висновок був, що їх може бути 15. У 1845 р. Браве довів тотожність двох із ґраток Франкгейма і правильно визначив число просторових ґраток – 14. Друга назва просторових ґраток – ґратки Браве. Ґратки, які відносяться до кубічної сингонії, тобто мають кубічну точкову групу симетрії – це проста кубічна гратка, об’ємноцентрована та гранецентрована. Тетрагональній точковій групі симетрії відповідають проста тетрагональна та об’ємноцентрована гратка. Тригональна група представлена ромбоедричною, або тригональною граткою Браве.
До ромбічної групи відносяться проста ромбічна гратка, об’ємноцентрована, базоцентрована та гранецентрована ґратки. Моноклінна є у вигляді простої ґратки та базоцентрованої. І, нарешті, триклинна система теж має лише просту гратку. Отже, всього 14 ґраток Браве. Розглянуті нами 7 сингоній і 14 просторових ґраток Браве вичерпують всі можливі випадки для просторових ґраток, які є, як ми вже згадували, математичною абстракцією.
Але у випадку базису довільної симетрії симетрія кристалу може бути нижче симетрії його просторової ґратки. Сказане пояснює рисунок. Просторова ґратка (а) на цьому рисунку має дзеркальну площину. Помістимо у вузли цієї ґратки молекули, що не мають цього елемента симетрії. Одержуємо кристал, що не має дзеркальної площини (б). Таким чином, базис понизив симетрію кристала відносно симетрії його просторової ґратки. Якщо між розмірами базису та розмірами основних векторів ґратки існують певні співвідношення, можуть додатися ще дві операції симетрії. Ми не будемо їх розглядати детально, просто занотуйте. 1. Гвинтові осі. Кристалічна структура із гвинтовою віссю переходить у саму себе при трансляції на вектор, який не належить до ґратки Браве, з наступним поворотом навколо осі, вздовж котрої відбувалася трансляція. Прикладом є болт. Якщо він має круглу шляпку без шліца, то це гвинтова вісь симетрії 2. Площини ковзання. Кристалічна структура з площиною ковзання переходить у саму себе при трансляції на вектор, який не належить до ґратки Браве, з наступним відбиттям у площині, до якої належить цей вектор. Ці додаткові операції симетрії призводять до того, що в кристалах збільшується кількість точкових і просторових груп симетрії. Якщо для кристалічної ґратки існують 7 сингоній (тобто точкових груп) і 14 ґраток Браве (просторових груп симетрії), то кристали можуть мати 32 точковігрупи симетрії і 230 просторових груп. Але розглядати їх ми не будемо і перейдемо до того, як можна використати наші знання про симетрію кристалу.
|

 чотирьох- або шестигранна призма. Анізотропія у таких кристалах виражена сильніше, ніж у кристалів вищої категорії.
чотирьох- або шестигранна призма. Анізотропія у таких кристалах виражена сильніше, ніж у кристалів вищої категорії.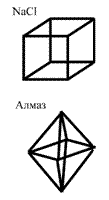 Кристали трьох розглянутих категорій поділяються на 7 систем, які називаються сингонії. У кожну сингонію входять кристали з однаковою точковою групою симетрії просторових ґраток. Неважко переконатися, що просторові ґратки кристалів однієї системи мають однакову точкову симетрію. Ось давайте порівняємо симетрію таких різних за властивостями матеріалів як сіль NaCl та алмаз. Гратка солі є кубічною, а алмазу – складається із рівнобічних трикутників. Вони мають:
Кристали трьох розглянутих категорій поділяються на 7 систем, які називаються сингонії. У кожну сингонію входять кристали з однаковою точковою групою симетрії просторових ґраток. Неважко переконатися, що просторові ґратки кристалів однієї системи мають однакову точкову симетрію. Ось давайте порівняємо симетрію таких різних за властивостями матеріалів як сіль NaCl та алмаз. Гратка солі є кубічною, а алмазу – складається із рівнобічних трикутників. Вони мають: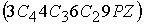 , отже, вони належать до однієї сингонії.
, отже, вони належать до однієї сингонії.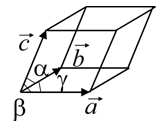 Розподіл кристалів на сингонії визначає вибір кристалографічної системи координат із знайомою нам трійкою базисних векторів
Розподіл кристалів на сингонії визначає вибір кристалографічної системи координат із знайомою нам трійкою базисних векторів 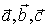 , або їх довжини та кути між ними
, або їх довжини та кути між ними 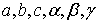 , які вводяться наступним чином (рис.). Кут
, які вводяться наступним чином (рис.). Кут  лежить у площині, до якої не належить вектор
лежить у площині, до якої не належить вектор 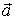 , і т.д.
, і т.д.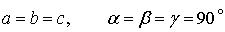 .
.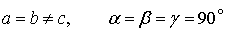 .
. .
. .
. розтягти за протилежні бічні грані, так щоб всі сторони комірки стали різними, а кути залишилися прямими, отримаємо ромбічну структуру
розтягти за протилежні бічні грані, так щоб всі сторони комірки стали різними, а кути залишилися прямими, отримаємо ромбічну структуру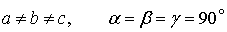 .
. .
. .
.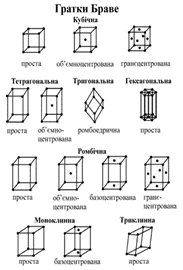 Гексагональна група –теж має лише єдину просту гратку.
Гексагональна група –теж має лише єдину просту гратку. Для побудови за допомогою просторової ґратки кристала в її вузли потрібно помістити базис. У випадку сферично-симетричного базису симетрія кристалу буде співпадати із симетрією його просторової ґратки.
Для побудови за допомогою просторової ґратки кристала в її вузли потрібно помістити базис. У випадку сферично-симетричного базису симетрія кристалу буде співпадати із симетрією його просторової ґратки. порядку. Якщо кругла із шліцом – гвинтова вісь 2 порядку. Якщо шляпка шестигранна – гвинтова вісь 6 порядку.
порядку. Якщо кругла із шліцом – гвинтова вісь 2 порядку. Якщо шляпка шестигранна – гвинтова вісь 6 порядку.


