В случайном потенциальном рельефеВ случае плотного газа центров (источников слабого рассеяния) потенциальная энергия электрона в поле каждого центра характеризуется радиусом действия
относительно единого начала отсчета энергии Исходя из формы атомных потенциальных ям
Вид потенциальной энергии электрона в поле отдельного атома определяет также и автокорреляционную функцию:
с помощью которой можно найти бинарную функцию распределения и другие статистические характеристики поля В выражении (6.39) для нас существенно то, что функция
которая L по порядку величины сравнима с «радиусом действия» каждого отдельного атома. Того же порядка будет и минимальная длина волны, соответствующая спектральной области 0 < q < Рассмотрим теперь электрон с энергией E, перемещающийся в случайном поле
Если на каждом отрезке классической траектории укладывается много длин волн электрона, то мы вправе воспользоваться квазиклассическим приближением для решения уравнения Шредингера. В рамках разумных допущений относительно вида функции
В указанных условиях плотность состояний электрона с хорошей точностью дается приближением Томаса - Ферми: в той области, где потенциальная энергия электрона есть V. Плотность числа состояний электронов выражается следующим образом:
Соответственно, интегральная плотность состоянийвыражается следующим образом:
Учтем теперь, что значения
Соответственно, в квазиклассическом предельном случае плотность состояний электрона в случайном гауссовом поле
Рис. 6.9. Плотность состояний в приближении Томаса - Ферми для гауссова случайного потенциала.
Поведение этой величины как функции энергии (ее можно выразить аналитически с помощью функции параболического цилиндра) изображено на рис. 6.9 сплошной кривой. В области высоких энергий
Однако при энергиях ниже уровня, принятого нами за нулевой, плотность состояний не обращается в нуль; асимптотически, при
Иначе говоря, у плотности состояний появляется модифицированный гауссов хвост, отвечающий электронным уровням в глубоких потенциальных ямах. В этом приближении кинетические характеристики электронов в рассматриваемой системе определяются главным образом тем, что классический электрон не способен проникнуть внутрь любой области, в которой потенциальная энергия Интуитивно ясно, что при переходе от низких энергий к более высоким топология «дозволенных» областей должна изменяться. Представим себе «рельеф», заливаемый водой. Для малых энергий E заполнены лишь самые глубокие минимумы, образующие изолированные «пруды» или «озера». При таких значениях энергии, следовательно, все классические или квазиклассические электроны будут локализованы. Однако, с подъемом уровня воды, эти озера начнут разрастаться и смыкаться друг с другом, в конечном счете, образуя связный океан, омывающий всю систему.
а
б
Рис. 6.10. а - изоэнергетические контуры в случайном потенциале; б - разрез АА потенциального рельефа, на котором видны области локализованных состояний.
Выше критического уровня Задача об определении порогового значения Аналогично решению порога протекания Это рассуждение не удается обобщить на случай трех измерений. Но вполне правдоподобно, что в континуальной модели протекание становится возможным, когда «разрешенные» области заполняют ту же критическую долю объема, что и в случае регулярных решеток, составленных из шаров. В дальнейшем будет показано, что эта величина оказывается приблизительно одинаковой для нескольких решеток различной структуры. Кроме того, гипотеза о том, что для трехмерных случайных полей
согласуется с результатом численного расчета по методу Монте-Карло. Если теперь проинтегрировать распределение (6.46), выбрав верхний предел интегрирования так, чтобы объем разрешенных областей под соответствующим уровнем составлял указанную долю полного объема, то мы получим
Это соотношение дает приближенный рецепт определения порога протекания в гауссовом случайном поле с дисперсией
|

 . Последний достаточно велик для того, чтобы охватить много атомных сфер радиуса
. Последний достаточно велик для того, чтобы охватить много атомных сфер радиуса  , однако глубина ямы здесь недостаточна для образования связанного состояния электрона. Полная потенциальная энергия теперь представляет собой результат суперпозиции многих перекрывающихся вкладов, и потому ведет себя подобно гауссову случайному полю. Будем считать, что среднее значение потенциальной энергии электрона в отдельном атоме равно нулю –
, однако глубина ямы здесь недостаточна для образования связанного состояния электрона. Полная потенциальная энергия теперь представляет собой результат суперпозиции многих перекрывающихся вкладов, и потому ведет себя подобно гауссову случайному полю. Будем считать, что среднее значение потенциальной энергии электрона в отдельном атоме равно нулю –  . Тогда, как это делалось в разделе «континуальный беспорядок», мы можем рассматривать величину
. Тогда, как это делалось в разделе «континуальный беспорядок», мы можем рассматривать величину  как непрерывную случайную функцию, значения которой распределены с вероятностью
как непрерывную случайную функцию, значения которой распределены с вероятностью (6.37)
(6.37)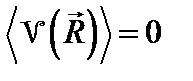 .
. , можно найти ширину распределения,
, можно найти ширину распределения,  . Она получается из соотношения:
. Она получается из соотношения: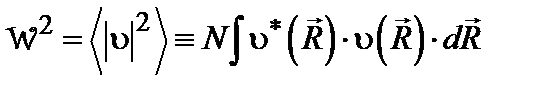 . (6.38)
. (6.38) , (6.39)
, (6.39) (6.40)
(6.40) удовлетворяет обычным предельным соотношениям и характеризуется длиной корреляции
удовлетворяет обычным предельным соотношениям и характеризуется длиной корреляции , (6.40)
, (6.40) волновых чисел в Фурье-представлении потенциальной энергии.
волновых чисел в Фурье-представлении потенциальной энергии. , то электрон всегда пролетает над горбами потенциального рельефа. В этих условиях можно с достаточной точностью решить уравнение Шредингера, рассматривая V как возмущение, искажающее волновые функции свободных электронов. Этот подход, однако, неправомерен при более низких энергиях, когда в некоторых областях величина
, то электрон всегда пролетает над горбами потенциального рельефа. В этих условиях можно с достаточной точностью решить уравнение Шредингера, рассматривая V как возмущение, искажающее волновые функции свободных электронов. Этот подход, однако, неправомерен при более низких энергиях, когда в некоторых областях величина  Рис. 6.8. Квазиклассический электрон в случайном потенциале неспособен проникнуть сквозь потенциальные барьеры.
Рис. 6.8. Квазиклассический электрон в случайном потенциале неспособен проникнуть сквозь потенциальные барьеры. можно показать, что характерный размер «топографических деталей»
можно показать, что характерный размер «топографических деталей»  квазиклассическое приближение оправдано, когда L превосходит характерную длину волны де Бройля
квазиклассическое приближение оправдано, когда L превосходит характерную длину волны де Бройля  , т. е., если воспользоваться атомными единицами
, т. е., если воспользоваться атомными единицами  , когда выполняется неравенство
, когда выполняется неравенство . (6.41)
. (6.41) .
. . (6.42)
. (6.42) распределены с вероятностью
распределены с вероятностью  . Поэтому интегральная плотность состояний с энергией, не превышающей E, для системы в целом должна быть равна
. Поэтому интегральная плотность состояний с энергией, не превышающей E, для системы в целом должна быть равна . (6.43)
. (6.43) . (6.44)
. (6.44)
 она приближается к обычной зависимости, характерной для свободных электронов (штриховая кривая).
она приближается к обычной зависимости, характерной для свободных электронов (штриховая кривая). . (6.45)
. (6.45) , она описывается выражением:
, она описывается выражением: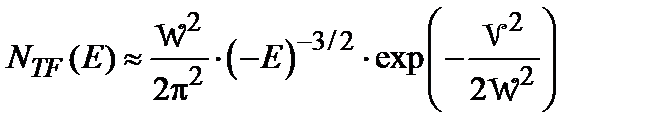 . (6.46)
. (6.46)
 в системе имеются делокализованные электронные состояния, и она способна проводить электрический ток по цепи дозволенных для движения каналов.
в системе имеются делокализованные электронные состояния, и она способна проводить электрический ток по цепи дозволенных для движения каналов. для протекания по континууму точно решается в случае пространства двух измерений. Поскольку потенциальная энергия
для протекания по континууму точно решается в случае пространства двух измерений. Поскольку потенциальная энергия  в задаче о протекании по узлам плоской сетки с треугольными ячейками можно сказать, что одновременное протекание по областям обоих указанных типов невозможно. Таким образом, уровень протекания должен быть
в задаче о протекании по узлам плоской сетки с треугольными ячейками можно сказать, что одновременное протекание по областям обоих указанных типов невозможно. Таким образом, уровень протекания должен быть  . Это соответствует ситуации, в которой разрешенная область занимает точно половину всего объема.
. Это соответствует ситуации, в которой разрешенная область занимает точно половину всего объема. (6.47)
(6.47) (6.48)
(6.48) . Его можно рассматривать и как оценку положения края подвижности для электронов в такой системе.
. Его можно рассматривать и как оценку положения края подвижности для электронов в такой системе.


