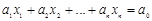Точечно-векторное аффинное пространствоОпределение. Пусть некоторое множество Множество 1. Каждая пара точек А 1 и A 2, заданных в определенном порядке, определяет единственный вектор 2. Для каждой точки А 1, и каждого вектора 3. Если Пространство Пример. Данному определению удовлетворяет, очевидно, обычное геометрическое пространство, в котором векторы вводятся как упорядоченные пары точек. Вторая аксиома соответствует возможности отложить любой вектор из произвольной точки, а третья аксиома соответствует определению сложения векторов. 4.1. Система координат в пространстве Если в пространстве Vn зафиксировать некоторую точку O, то в силу свойств 1 и 2 между всеми остальными точками и векторами устанавливается взаимно однозначное соответствие. Вектор Определение. Системой координат в пространстве Vn, называется совокупность фиксированной точки O и некоторого базиса Координатами вектора Координатами точки А в данной системе ко- Всякие два базиса пространства Vn
где вектор-столбцы матриц перехода Если даны две системы координат O,
где 4.2.Прямая и плоскость в Vn Определение. Пусть в аффинном пространстве Vn заданы собственное подпространство L и фиксированный вектор
называется плоскостью в Vn. Размерностью плоскости X называется размерность соответствующего подпространства Одномерная плоскость пространства Vn называется прямой линией. Плоскость размерности Две плоскости называются совпадающими, если они состоят из одних и тех же точек (векторов) пространства; в противном случае они называются несовпадающими. Множество точек n -мерного пространства, принадлежащих как плоскости X 1, так и плоскости X 2, называется их пересечением, а сами плоскости X 1 и X 2 пересекающимися, если Две несовпадающие плоскости Из определения плоскости следует, что всякая плоскость является линейным многообразием. Всякая k -мерная плоскость
где
ранга n - k, где В частности, всякая прямая задается либо системой линейных уравнений ранга
где
Наконец, в координатной форме можно записать каноническое уравнение прямой
где Всякая гиперплоскость задается одним линейным уравнением
|

 состоит из элементов двух типов, которые будем называть «точками» и «векторами». Пусть при этом множество векторов образует n -мерное линейное пространство, а множество точек не пусто.
состоит из элементов двух типов, которые будем называть «точками» и «векторами». Пусть при этом множество векторов образует n -мерное линейное пространство, а множество точек не пусто. .
. существует единственная точка A 2, такая, что
существует единственная точка A 2, такая, что 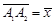 .
.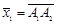 и
и 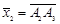 , то
, то 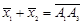 .
.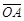 называется радиус-вектором точки А относительно точки O.
называется радиус-вектором точки А относительно точки O. в Vn.
в Vn. связаны между собой формулами перехода
связаны между собой формулами перехода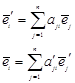
 и
и  состоят из координат векторов
состоят из координат векторов 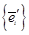 и
и  соответственно в базисах
соответственно в базисах 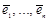 и
и 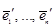 .
.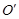 ,
, 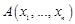 и
и 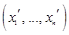 относительно этих систем координат связаны соотношениями
относительно этих систем координат связаны соотношениями ,
, 
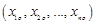 – координаты точки
– координаты точки 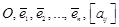 – матрица перехода.
– матрица перехода.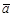 .Множество
.Множество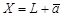
 .
.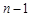 называется гиперплоскостью.
называется гиперплоскостью.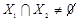 .
.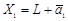 и
и 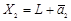 , полученные сдвигом одного и того же подпространства L, называются параллельными.
, полученные сдвигом одного и того же подпространства L, называются параллельными.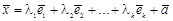 ,
,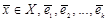 — базис в L,
— базис в L, 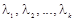 — произвольные числа, либо как линейное многообразие системой линейных неоднородных уравнений
— произвольные числа, либо как линейное многообразие системой линейных неоднородных уравнений
 — координаты вектора
— координаты вектора  .
.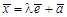
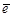 — направляющий вектор прямой, λ — параметр. Если
— направляющий вектор прямой, λ — параметр. Если 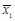 и
и 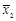 — радиус-векторы двух точек прямой, то можно записать уравнение прямой, проходящей через две данные точки
— радиус-векторы двух точек прямой, то можно записать уравнение прямой, проходящей через две данные точки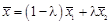 ,
,  ,
, — координаты некоторой фиксированной точки прямой;
— координаты некоторой фиксированной точки прямой; 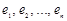 -координаты направляющего вектора
-координаты направляющего вектора