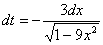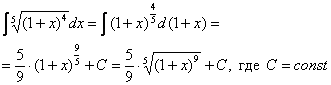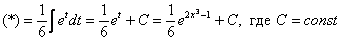Метод замены переменной в неопределенном интегралеПереходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле. Пример 5 Найти неопределенный интеграл. В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже говорили, для решения интеграла нам приглянулась табличная формула Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой. Итак: Действие следующее. После того, как мы подобрали замену, в данном примере, Так как
После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко: В итоге:
Чистовое оформление рассмотренного примера должно выглядеть примерно так: “ Проведем замену:
Значок Также всем рекомендую использовать математический знак При оформлении примера в тетради надстрочную пометку Внимание! В следующих примерах нахождение дифференциала А теперь самое время вспомнить первый способ решения: В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче. Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала. Пример 6 Найти неопределенный интеграл. Проведем замену:
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.
Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении. Пример 7 Найти неопределенный интеграл. Выполнить проверку. Пример 8 Найти неопределенный интеграл. Замена:
Готово. Пример 9 Найти неопределенный интеграл. Пример 10 Найти неопределенный интеграл. Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде. Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных. В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу
Замена:
Кстати, здесь не так сложно подвести функцию под знак дифференциала: Следует отметить, что для дробей вроде Вот еще пара типовых примеров для самостоятельного решения из той же оперы: Пример 11 Найти неопределенный интеграл. Пример 12 Найти неопределенный интеграл. Решения в конце урока. Пример 13 Найти неопределенный интеграл. Смотрим в таблицу производных и находим наш арккосинус: Общее правило: В данном случае: В этом примере нахождение
Таким образом: Вот здесь подвести функцию под знак дифференциала уже не так-то просто. Пример 14 Найти неопределенный интеграл. Пример для самостоятельного решения. Ответ совсем близко. Желаю успехов! Решения и ответы: Пример 3: Решение: Пример 4: Решение: Пример 7: Решение: Пример 9: Решение: Пример 11: Решение: Пример 12: Решение: Пример 14: Решение:
|
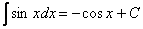, и всё дело хотелось бы свести к ней.
.
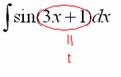
! Наверное, многие догадались, что если осуществляется переход к новой переменной 
, то в новом интеграле всё должно быть выражено через букву 
. С дифференциалами, думаю, дружба уже у всех налажена.
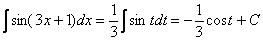
не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.
вместо фразы «из этого следует это». И коротко, и удобно.
обратной замены лучше выполнять простым карандашом.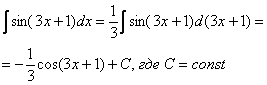
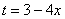(другую замену здесь трудно придумать)
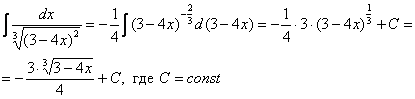
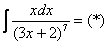
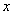мы выразим из той же замены 
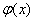и её производная 
: 
(функции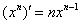 
, которая как раз понижает степень на единицу. А, значит, если обозначить за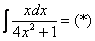 
, 
такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей.
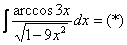
. У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную.
. Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения 
.
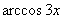– сложная функция.
