| x + 1
| x plus one
|
| x -1
| x minus one
|
| x ± 1
| x plus or minus one
|
| xy
| x y; x times y; x multiplied by y
|
| (x — y)
(x + y)
| x minus y, x plus y
|
| x/y
| x over y; x divided by y;
|
| x ÷ y
| x divided by y
|
| x = 5
| x equals 5; x is equal to 5
|
| x ≈ y
| x is approximately equal to y
|
| x ≡ y
| x is equivalent to y; x is identical with y
|
| x ≠ y
| x is not equal to y
|
| x > y
| x is greater than y
|
| x < y
| x is less than y
|
| x ≥ y
| x is greater than or equal to y
|
| x ≤ y
| x is less than or equal to y
|
| 0 < x < 1
| zero is less than x is less than 1; x is greater than zero and less than 1
|
| 0 ≤ x ≤ 1
| zero is less than or equal to x is less than or equal to 1; x is greater than or equal to zero and less than or equal to 1
|
| x²
| x squared
|
| x³
| x cubed
|
| x4
| x to the fourth; x to the power four
|
| xn
| x to the n; x to the nth; x to the power n
|
| x-n
| x to the minus n; x to the power of minus n
|
| √
| root x; square root x; the square root of x
|
| ∛
| the cube root of x
|
| ∜
| the fourth root of x
|

| the nth root of x
|
| (x + y)²
| x plus y all squared
|
| (x/y)²
| x over y all squared
|
| n!
| n factorial; factorial n
|
| x%
| x percent
|
| ∞
| infinity
|
| x ∝ y
| x varies as y; x is (directly) proportional to y
|
| x ∝ 1/y
| x varies as one over y; x is indirectly proportional to y
|
| ẋ
| x dot
|
| ẍ
| x double dot
|
| f(x) fx
| f of x; the function of x
|
| f'(x)
| f dash x; the (first) derivative of with respect to x
|
| f''x
| f double-dash x; the second derivative off with respect to x
|
| f'''(x)
| f triple-dash x; f treble-dash x; the third derivative off with respect to x
|
| f(4)
| f four x; the fourth derivative off with respect to x
|
| ∂v
| the partial derivative of v
|
| ∂v ∂θ
| delta v by delta theta, the partial derivative of v with respect to θ
|
| ∂ ² v ∂θ²
| delta two v by delta theta squared; the second partial derivative of v with respect to θ
|
| dv
| the derivative of v
|
| dv dθ
| d v by d theta, the derivative of v with respect to theta
|
| d ² v dθ²
| d 2 v by d theta squared, the second derivative of v with respect to theta,
|
| ∫
| integral
|
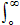
| integral from zero to infinity
|
| ∑
| sum
|

| the sum from i equals 1 to n
|
| w.r.t.
| with respect to
|
| logey
| log to the base e of y; log y to the base e; natural log (of) y
|
| ∴
| therefore
|
| ∵
| because
|
| →
| gives, approaches
|
| Δx → 0
| delta x approaches zero
|
| limΔx→0
| the limit as delta x approaches zero, the limit as delta x tends to zero
|
| LtΔx→0
| the limit as delta x approaches zero, the limit as delta x tends to zero
|
| m/sec
| metres per second
|
| x ∈ A
| x belongs to A; x is a member of A; x is an element of A
|
| x∉ A
| x does not belong to A; x is not a member of A; x is not an element of A
|
| A⊂ B
| A is contained in B; A is a proper subset of B
|
| A ⊆ B
| A is contained in B; A is a subset of B
|
| A ⋂ B
| A intersection B
|
| A ⋃ B
| A union B
|
| cos x
| cos x; cosine x
|
| sin x
| sine x
|
| tan x
| tangent x, tan x
|
| cosec x
| cosec x
|
| sinh x
| shine x
|
| cosh x
| cosh x
|
| tanh x
| than x
|
| |x|
| mod x; modulus x
|
| 18 ℃
| eighteen degrees Centigrade
|
| 70 ℉
| seventy degrees Fahrenheit
|