Алгоритм уменьшения ошибкиРассмотрим алгоритмы решения нелинейного интегрального уравнения Френеля, предназначенного для расчета фазовых оптических элементов, формирующих произвольное заданное распределение интенсивности когерентного монохроматического света в некоторой плоскости, перпендикулярной оптической оси. Такие алгоритмы являются адаптивными, т.к. новая оценка искомой функции на каждой итерации выбирается не только в соответствии с требуемой функцией интенсивности, но и в зависимости от предыдущей оценки. В скалярной теории дифракции комплексная амплитуда волны в плоскости оптического элемента
где
- функция импульсного отклика свободного пространства в приближении Френеля, z – расстояние между ДОЭ и плоскостью наблюдения. В уравнении (2.1) комплексная амплитуда Поскольку рассматриваются только фазовые оптические элементы, функция пропускания ДОЭ выбрана в виде
где Итеративный метод расчета фазы 1) выбирается начальная оценка фазы 2) осуществляется интегральное преобразование функции 3) результирующая комплексная амплитуда
4) вычисляется преобразование, обратное (2.1) относительно функции
5) полученная комплексная амплитуда
где Q – форма апертуры ДОЭ; 6) переход к шагу 2. Эта процедура повторяется до тех пор, пока ошибки – и – не перестанут значительно меняться:
Алгоритм ГС называют алгоритмом уменьшения ошибки потому, что было показано, что ошибки (2.7) и (2.8) с ростом числа итераций не возрастают. Однако, процесс сходимости алгоритма ГС конечен – в ходе начальных итераций ошибка быстро уменьшается, а все последующие итерации не приводят к ее заметному уменьшению.
|

 связана с комплексной амплитудой волны
связана с комплексной амплитудой волны  в плоскости формирования требуемого распределения интенсивности
в плоскости формирования требуемого распределения интенсивности  через интегральное преобразование:
через интегральное преобразование: , (2.1)
, (2.1)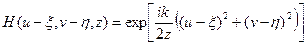 (2.2)
(2.2) в приближении тонкого оптического элемента (приближение транспаранта), которое не учитывает рефракцию лучей, равна произведению комплексной амплитуды
в приближении тонкого оптического элемента (приближение транспаранта), которое не учитывает рефракцию лучей, равна произведению комплексной амплитуды  на собственную функцию пропускания
на собственную функцию пропускания  ДОЭ:
ДОЭ:  .
. , где
, где  – заданная фаза ДОЭ. Задачу расчета фазовой функции ДОЭ
– заданная фаза ДОЭ. Задачу расчета фазовой функции ДОЭ  , (2.3)
, (2.3) - амплитуда освещающего пучка,
- амплитуда освещающего пучка,  ,
,  - фаза освещающего пучка.
- фаза освещающего пучка. , а также фазы
, а также фазы 
 при помощи уравнения (2.1)
при помощи уравнения (2.1) в плоскости формирования изображения заменяется на
в плоскости формирования изображения заменяется на  по правилу
по правилу , где
, где  ; (2.4)
; (2.4) ; (2.5)
; (2.5) в плоскости ДОЭ заменяется на
в плоскости ДОЭ заменяется на  по правилу
по правилу (2.6)
(2.6) , (2.7)
, (2.7) . (2.8)
. (2.8)


