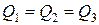Уравнение неразрывности (сплошности) потока
Установим общую зависимость, между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывности, движения, т. е. не образуется пустот, не заполненных жидкостью. Выделим внутри потока элементарный параллелепипед объемом dV = dx dy dz, ребра которого ориентированы параллельно осям координат (рис. 1). Пусть составляющая скорости потока вдоль оси х в точках, лежащих на левой грани параллелепипеда площадью dS = dy dz, равна wx Тогда, согласно уравнению расхода, через эту грань в параллелепипед войдет вдоль оси х за единицу времени масса жидкости r wx dy dz, а за промежуток времени dt – масса жидкости Mx = r wx dy dz dt, (1) где r – плотность жидкости на левой грани параллелепипеда. На противоположной (правой) грани параллелепипеда скорость и плотность жидкости могут отличаться от соответствующих величин на левой грани и будут равны Тогда через правую грань параллелепипеда за то же время dt выйдет масса жидкости
Рис. 1. К выводу дифференциального уравнения неразрывности потока
Приращение массы жидкости в параллелепипеде вдоль оси x
Если составляющие скорости вдоль осей у и z равны wy и wz соответственно, то приращения массы в элементарном объеме вдоль этих осей по аналогии составят:
Общее накопление массы жидкости в параллелепипеде за время dt равно сумме ее приращений вдоль всех осей координат:
Вместе с тем изменение массы в полностью заполненном жидкостью объеме параллелепипеда возможно только вследствие изменения плотности жидкости в этом объеме. Поэтому
Приравнивая оба выражения dM, сокращая на (– dx dy dz dt) и перенося
Уравнение (8) представляет собой дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости. Уравнение (8) может быть записано и в несколько иной форме. Проводя дифференцирование произведения
или
где В установившемся потоке плотность не изменяется во времени, т, е.
Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока при скоростях, значительно меньших скорости звука, r = const и, следовательно
Уравнение (12) является дифференциальным уравнением неразрывности потока несжимаемой жидкости. Сумма изменений скорости вдоль осей координат в левой части уравнения (12) называется дивергенцией вектора скорости и обозначается через div w. Поэтому данное уравнение можно представить как
Для того чтобы перейти от элементарного объема ко всему объему жидкости, движущейся сплошным потоком по трубопроводу переменного сечения (рис. 13), проинтегрируем дифференциальное уравнение (11). Если бы площадь сечения трубопровода не изменялась, то для установившегося однонаправленного движения (в направлении оси х) интегрирование уравнения (42) дало бы зависимость
где w – средняя скорость жидкости.
Рис. 2. К выводу уравнения постоянства расхода
Если же площадь сечения S трубопровода переменна, то, интегрируя также по площади, получим
Для трех различных сечений (1—1, 2 — 2 и 3—3) трубопровода, изображенного на рис. 2, имеем
или
где Выражение (13) или (14) представляет собой уравнение неразрывности (сплошности) потока в его интегральной форме для установившегося движения. Это уравнение называется также уравнением постоянства расхода. Согласно уравнению постоянства расхода, при установившемся движении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одна и та же масса жидкости. Для капельных жидкостей
Следовательно
или
где Q = wS – объемный расход жидкости, м3/с. Из уравнения (15а) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений. Согласно уравнению (15), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока.
|

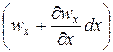 и
и  .
. . (2)
. (2)
 . (3)
. (3) . (4)
. (4) . (5)
. (5) . (6)
. (6) . (7)
. (7) в левую часть уравнения окончательно получим
в левую часть уравнения окончательно получим (8)
(8) , получим
, получим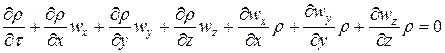 (9)
(9) , (10)
, (10) – субстанциональная производная плотности.
– субстанциональная производная плотности. (11)
(11) . (12)
. (12) (12a)
(12a) ,
,
 (13)
(13) (14)
(14)
 – массовый расход жидкости, кг/с.
– массовый расход жидкости, кг/с.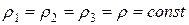 , и уравнение (14) принимает вид
, и уравнение (14) принимает вид (15)
(15) (15a)
(15a)