ФУНКЦИОНАЛЬНЫЕ РЯДЫ
где T, T0 – кинетическая энергия системы соответственно в конечный и начальный моменты времени;
В рассматриваемой задаче система состоит из катка, груза, блока и нити. Система сил, действующих на систему, включает активные силы Q, P, F, реакции связей NA, NB, Fсц, Fтр, Rx, Ry и момент трения в блоке M. Найдем сумму работ всех внешних сил системы на соответствующих перемещениях точек их приложения:
Работы сил NА и NB равны нулю, так как направления этих сил составляют прямой угол с направлениями перемещений точек их приложения. Работа силы сцепления Fсц и работы реакций Rx и Rу равны нулю, так как эти силы приложены к неподвижным точкам. Работы сил F, Р, Q, Fтр и пары сил с моментом М определим следующим образом:
После суммирования получим
Рассматриваемая механическая система состоит из абсолютно твердых тел, соединенных идеальной нитью. Для таких систем с идеальными связями сумма работ всех внутренних сил равна нулю
Рассчитаем кинетическую энергию системы в начальном и конечном положениях. По условию задачи система в начальный момент находилась в покое, следовательно, ее кинетическая энергия в этот момент равна нулю T0=0. Кинетическая энергия груза А, движущегося поступательно, равна
где Кинетическая энергия катка В, совершающего плоское движение, равна
где vC – скорость центра масс С катка,
wВ – угловая скорость катка, Кинетическая энергия системы равна сумме кинетических энергий всех тел, входящих в нее:
Подставляя выражения (2) – (4) в формулу (1), выражающую теорему об изменении кинетической энергии системы, получим
откуда искомая скорость груза А, в момент, когда он переместится на расстояние 3 м, равна
Список литературы Основная: 1. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов / 19-е изд., стер.- М.: Высш.шк., 2009.- 416 с.: ил. 2. Мещерский И.В. Задачи по теоретической механике: Учебное пособие, 50-е изд., стер. / Под ред. В.А. Пальмова, Д.Р. Меркина.- СПб.: Издательство «Лань», 2010.-448 с.: ил.
Дополнительная: 1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах: Учеб. пособ. – М.: Политехника, 1995 – 670с. 2. Голубев Ю.Ф. Основы теоретической механики: Учеб. для вузов. – М.: Изд-во МГУ, 1992. - 524 с. 3. Сборник задач по теоретической механике: Учеб. пособие для студентов вузов / Будник Ф.Г., Зингерман Ю.М., Зеленский Е.И.; под ре. Кельзона А.С. – Высш. шк., 1987. – 176 с. 4. Никитин Е.М. Теоретическая механика для техникумов.- 12-е изд., испр.- М.: Наука. Гл.ред.физ.-мат.лит., 1988.- 336 с. 5.Техническая механика: Учеб. для техникумов / Эрдеди А.А. и др.- 2-е изд. перераб.- М., Высш. школа, 1980.- 446 с., ил.
Задания и методические указания к выполнению контрольных работ по дисциплине «Теоретическая механика»
Подписано в печать. Формат 60х84/16. Бумага для множ. аппаратов. Печать плоская. Усл. печ. л. ____. Уч.- изд. л.___. Тираж____ экз. Заказ____ ФГАОУ ВПО «Российский государственный профессионально-педагогический университет, Екатеринбург, ул. Машиностроителей, 11.
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Основные понятия
который может быть как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью
Действительные (или комплексные) числа Ряд (2.2) разложен по степеням х. Рассматривают также степенной ряд, разложенный по степеням
где Ряд (2.3) легко приводится к виду (2.2), если положить Область сходимости степенного ряда (2.2) содержит по крайней мере одну точку х = 0 (ряд (2.3) сходится в точке Теорема 2.1 (Абеля). Если степенной ряд (2.2) сходится при Следствие. Если ряд (2.2) расходится при х = Из теоремы Абеля следует, что если Интервал (-|
Отметим, что на концах интервала сходимости (т. е. при х = R и при х = -R) сходимость ряда проверяется в каждом случае отдельно. Радиус сходимости степенного ряда (2.2) находится по формулам
1) интервал сходимости степенного ряда (2.3) находят из неравенства | 2) если степенной ряд содержит не все степени х, т.е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (2.4) и (2.5)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда. Пример 9. Найти область сходимости ряда Решение: Воспользуемся формулой (2.4), с учетом, что
Следовательно, данный ряд абсолютно сходится на всей числовой оси. Пример 10. Найти область сходимости ряда Решение: Находим радиус сходимости ряда по формуле (2.4).
Следовательно, ряд сходится при При
который сходится по признаку Лейбница (см. пример 8). При
Итак, областью сходимости исходного ряда является промежуток [-4; 0). Пример 11. Найти область сходимости ряда
Решение: Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:
Ряд абсолютно сходится, если При При Следовательно, областью сходимости исходного ряда является отрезок [-1; 1].
|

 Условие. Однородный каток В весом Q=4 кН и радиусом R и груз А весом Р=2 кН, соединенные гибкой нерастяжимой и невесомой нитью, помещены на шероховатую поверхность, наклоненную к горизонту под углом a=300 (рис. 3.9). Нить переброшена через невесомый блок О радиусом 30 см. К свободному концу нити приложена сила F, линейно зависящая от величины перемещения s: F=9,0+0,15×s (кН). Каток катится без скольжения; коэффициент трения скольжения груза о плоскость f=0,1, момент сил сопротивления в подшипнике блока М=300 Н м. Определить скорость груза А, когда он переместится на величину s=3 м. В начальный момент система находилась в покое.
Условие. Однородный каток В весом Q=4 кН и радиусом R и груз А весом Р=2 кН, соединенные гибкой нерастяжимой и невесомой нитью, помещены на шероховатую поверхность, наклоненную к горизонту под углом a=300 (рис. 3.9). Нить переброшена через невесомый блок О радиусом 30 см. К свободному концу нити приложена сила F, линейно зависящая от величины перемещения s: F=9,0+0,15×s (кН). Каток катится без скольжения; коэффициент трения скольжения груза о плоскость f=0,1, момент сил сопротивления в подшипнике блока М=300 Н м. Определить скорость груза А, когда он переместится на величину s=3 м. В начальный момент система находилась в покое.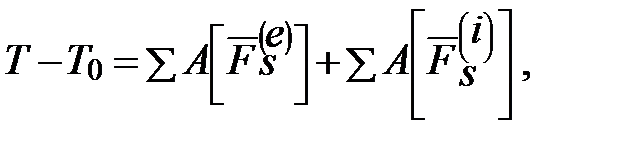 (1)
(1)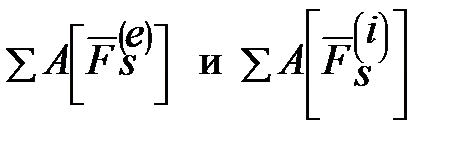 – суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.
– суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.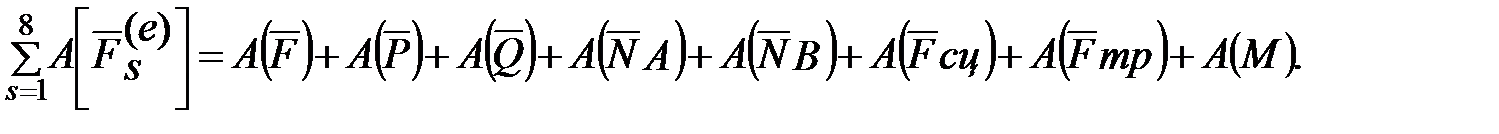
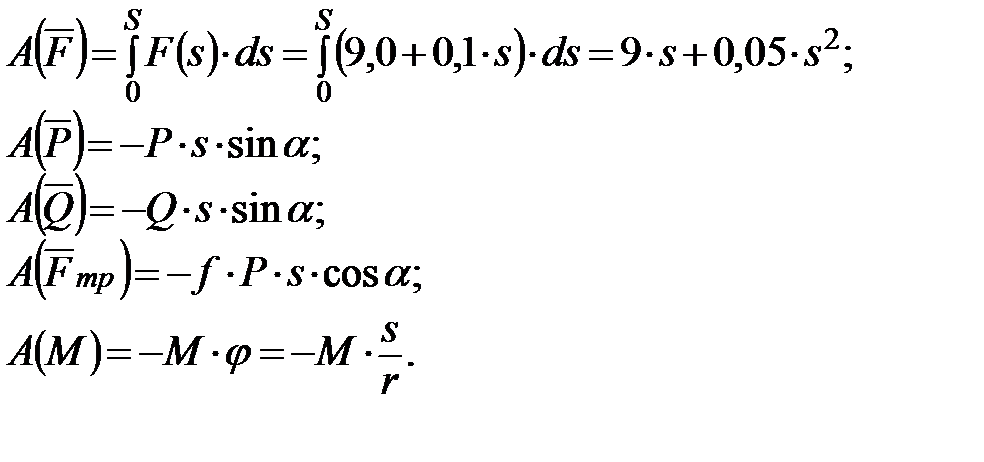
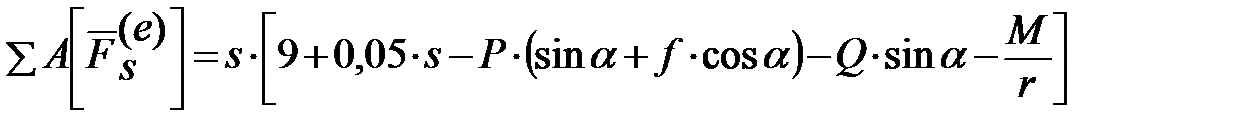 . (2)
. (2) . (3)
. (3)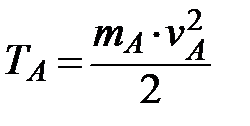 ,
,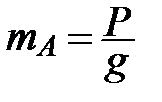 – масса груза А;
– масса груза А; 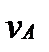 – скорость груза.
– скорость груза. ,
,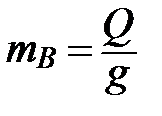 – масса катка В;
– масса катка В; ;
;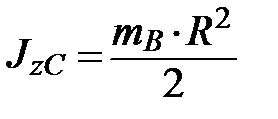 – момент инерции катка относительно оси, проходящей через его центр масс;
– момент инерции катка относительно оси, проходящей через его центр масс; .
.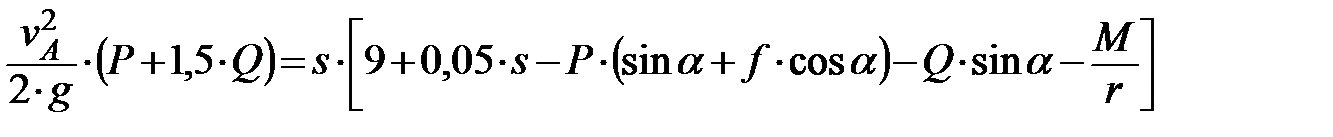 (4)
(4) ,
,
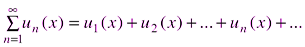
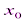 , получим числовой ряд:
, получим числовой ряд: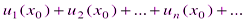 ,
,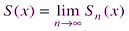 , где
, где 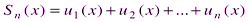 – частичная сумма ряда.
– частичная сумма ряда.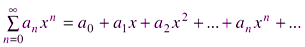 (2.2)
(2.2)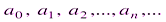 называются коэффициентами ряда (2.2),
называются коэффициентами ряда (2.2), 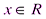 – действительная переменная.
– действительная переменная.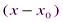 , т.е. ряд вида
, т.е. ряд вида ,(2.3)
,(2.3)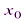 – некоторое постоянное число.
– некоторое постоянное число.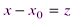 . Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (2. 2).
. Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (2. 2).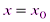 ).
).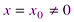 , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству | х | < |
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству | х | < |  |.
|.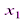 , то он расходится и при всех х, удовлетворяющих неравенству | х | > |
, то он расходится и при всех х, удовлетворяющих неравенству | х | > | 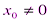 есть точка сходимости степенного ряда, то интервал (-|
есть точка сходимости степенного ряда, то интервал (-| 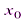 |;|
|;| 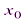 ||) весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (2.2) расходится.
||) весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (2.2) расходится. |;|
|;| 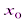 |) называют интервалом сходимости степенного ряда. Положив |
|) называют интервалом сходимости степенного ряда. Положив | 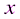 |< R, ряд (2.2) абсолютно сходится, а при |
|< R, ряд (2.2) абсолютно сходится, а при |  |> R – расходится (рисунок 1).
|> R – расходится (рисунок 1).
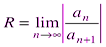 ,
,
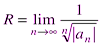 .
.
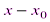 |< R; он имеет вид (
|< R; он имеет вид (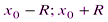 );
); .
.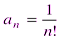 ,
, 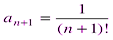 :
: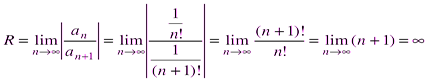 .
.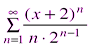 .
.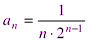 ,
, 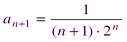 ;
;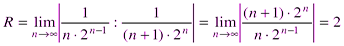 .
.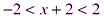 , т.е. при
, т.е. при 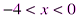 .
.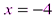 имеем ряд
имеем ряд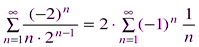 ,
, имеем расходящийся ряд
имеем расходящийся ряд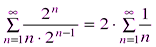 .
.
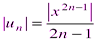 ,
, 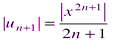 ,
,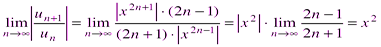 .
. < 1 или
< 1 или 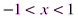 . Исследуем поведение ряда на концах интервала сходимости.
. Исследуем поведение ряда на концах интервала сходимости.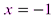 имеем ряд
имеем ряд 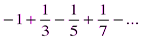 , который сходится по признаку Лейбница.
, который сходится по признаку Лейбница.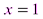 имеем ряд
имеем ряд 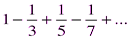 – это тоже сходящийся лейбницевский ряд.
– это тоже сходящийся лейбницевский ряд.


