Тема 10 Доверительная вероятность. Интервальные оценки
При выборке сравнительного небольшого объема точечная оценка может значительно отличаться от оцениваемого параметра. По этой причине следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами- концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. Доверительной вероятностью или надежностью оценки параметра d есть положительное число, которое характеризует точность оценки; чем меньше d, тем оценка точнее. Заменим неравенство
Доверительный интервал для оценки математического ожидания а нормального распределения при большом объеме выборки ( В этом случае среднее значение измеряемого параметра генеральной совокупности
где
n -объём выборки. По таблице значений функции Лапласа можно определить
При малом числе наблюдений (объём выборки меньше 30) точечная оценка в значительной мере случайна, и возможна только интервальная оценка. В этом случае недостаток информации о генеральной совокупности приводит к значительному расширению доверительного интервала. Точность оценки находится из соотношения:
где
Пример 3. Собраны данные о товарообороте Х (ден. ед.) 100 однотипных магазинов и получено следующее распределение (табл.1). 1. Построить гистограмму плотности относительных частот для наблюдаемых значений признака Х. 2. Составить дискретный вариационный ряд и статистическое распределение выборки. 3. Найти точечные характеристики выборки: 4. Найти доверительный интервал для оценки математического ожидания с заданной доверительной вероятностью Табл. 1
1. Для построения гистограммы относительных частот Табл. 2
Гистограмма относительных частот:
2. Для составления дискретного вариационного ряда найдем середины интервалов Табл. 3
Объем выборки 3. Найдем среднюю выборочную: Найдем выборочную дисперсию: 4. По заданной доверительной вероятности Вычислим точность оценки по формуле Точность оценки
Таким образом, если проведено достаточно большое число наблюдений случайной величины
Пример 4. Собраны данные о квартальной доходности акций нескольких компаний:
Полагая, что изменчивость доходности описывается законом нормального распределения, найти доверительный интервал для доходности акций на уровне надёжности Составим расчётную таблицу для нахождения
Найдём по приложению 3 коэффициент доверия Т(15; 0,95)=2,15 и точность оценки
4,5-0,727< 3,773< Cредняя доходность акций с надёжностью
|

 по
по  называют вероятность g, с которой осуществляется неравенство
называют вероятность g, с которой осуществляется неравенство  , то есть
, то есть  .
. равносильным ему двойным неравенством:
равносильным ему двойным неравенством:  . Тогда доверительную вероятность запишем как:
. Тогда доверительную вероятность запишем как:  Это соотношение понимают следующим образом: вероятность того, что интервал
Это соотношение понимают следующим образом: вероятность того, что интервал  заключает в себе неизвестный параметр
заключает в себе неизвестный параметр  . Интервал (
. Интервал ( называют доверительным интервалом.
называют доверительным интервалом. ).
). будет отличаться от выборочного значения
будет отличаться от выборочного значения  на величину
на величину  . При заданной доверительной вероятности
. При заданной доверительной вероятности  интервал имеет вид:
интервал имеет вид: ,
, - точность интервальной оценки,
- точность интервальной оценки, -среднее квадратическое отклонение, найденное по данным выборки,
-среднее квадратическое отклонение, найденное по данным выборки, из условия
из условия
 .
. ,
, “исправленное” стандартное отклонение признака X;
“исправленное” стандартное отклонение признака X; доверительная вероятность;
доверительная вероятность; коэффициент доверия для заданного объёма выборки n (см. приложение 3).
коэффициент доверия для заданного объёма выборки n (см. приложение 3).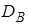
 .
. .
. (
( ) построим расчетную таблицу 2:
) построим расчетную таблицу 2:
 ,
,  т.д. Построим статистическое распределение выборки в таблице 3, в которой проведем расчеты для нахождения
т.д. Построим статистическое распределение выборки в таблице 3, в которой проведем расчеты для нахождения  ,
, 
 .
. .
. ден.ед.
ден.ед. и среднее квадратическое отклонение
и среднее квадратическое отклонение  .
. ; тогда
; тогда  .
. , следовательно, доверительный интервал для оценки математического ожидания будет равен:
, следовательно, доверительный интервал для оценки математического ожидания будет равен: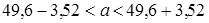 ;
;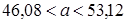 .
. (товарооборот магазина), то в
(товарооборот магазина), то в  случаев доверительный интервал
случаев доверительный интервал  покроет математическое ожидание значения товарооборота; в
покроет математическое ожидание значения товарооборота; в  случаев математическое ожидание может выйти за границы доверительного интервала.
случаев математическое ожидание может выйти за границы доверительного интервала. =0,95.
=0,95. и
и  :
:

 - средняя доходность акций,
- средняя доходность акций, - исправленное стандартное отклонение.
- исправленное стандартное отклонение. . Тогда доверительный интервал
. Тогда доверительный интервал
 <4,5+0,727
<4,5+0,727 будет находится в интервале от 3,773% до 5,227%.
будет находится в интервале от 3,773% до 5,227%.


