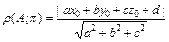Кривые второго порядка, их канонические уравнения, параметрыКривые второго порядка – это линии плоскости, уравнения которых по совокупности переменных х и у, являются уравнением второго порядка. ax2+by2+cxy+dx+ey+f=0, где a, b, c не все раны 0. Существует три типа таких кривых: эллипс (окружность), гипербола, парабола. Окружность – это множество точек плоскости, каждая из которых равноудалена от центра С. Если C(x0; y0), М(х, у) точка окружности с текущими координатами и СМ=r, то уравнение окружности имеет вид: (x–x0)2+(y–y0)2=r2 Если С совпадает с началом координат, СºО,то x2+y2=r 2. Эллипс – это множество точек плоскости, удовлетворяющих условию: сумма расстояний до двух данных точек (фокусов) есть величина постоянная Если фокусы F1 и F2 расположить на оси ОХ так, чтобы F1O=OF2, F1F2=2с, a |MF1|+|MF2|=2a, a>с, тогда каноническое уравнение эллипса: Из уравнения видно, что кривая симметрична относительно осей ОХ и ОУ. Эллипс имеет 4 вершины: А(0;0), A2(–a;0), B1(0;b), B2(0;–b).
Эллипс имеет две директрисы – это прямые, перпендикулярные фокальной оси, находящейся на расстоянии Если центр эллипса находится в точке С(х0, у0), то его уравнение: Гипербола – множество точек плоскости, для которых разность расстояний для двух данных точек (фокусов) есть величина постоянная.
Так как Гипербола имеет две вершины: А1(0,0), А2(-а,0).
Если расстояние от фокуса до директрисы равно К и если фокус лежит на оси Ох, а директриса перпендикулярна Ох, то каноническое уравнение параболы имеет вид: у2=2рх у2=2рх
Если фокус принадлежит ОУ: х2=2ру х2= –2ру
Если вершина находится в т. С(х0, у0), то каноническое уравнение имеет вид: (x–x0)2= ±2p(y–y0) (y–y0)2= ±2p(x–x0) Различные уравнения плоскости
Если дана точка. А(x0; y0; z0) и даны два направляющих вектора
a(x–x0)+b(y–y0)+c(z–z0)=0 (3) Если раскроем скобки в последнем равенстве, то получим общее уравнение плоскости: ax+by+cz+d=0 (4),
Взаимное расположение плоскостей. Пусть π 1 || π 2 Û π 1º π 2 Û π 1^ π 2 Û a1a2+b1b2+c1c2=0 Расстояние от т. А(x0; y0; z0) до плоскости π: ax+by+cz+d=0 вычисляется по формуле
|

 : F1M+F2M=const
: F1M+F2M=const , где F1F2 – фокальная ось, а – большая полуось, b – малая полуось, а b2=a2–c2.
, где F1F2 – фокальная ось, а – большая полуось, b – малая полуось, а b2=a2–c2. |x|<a;
|x|<a; 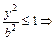 |y|<b, т.е. эллипс – фигура ограниченная и лежит внутри прямоугольника со сторонами 2а и 2b. Этот прямоугольник называется основным.
|y|<b, т.е. эллипс – фигура ограниченная и лежит внутри прямоугольника со сторонами 2а и 2b. Этот прямоугольник называется основным. Эксцентриситет эллипса
Эксцентриситет эллипса  характеризует вытянутость эллипса вдоль оси Ох. При с®0,
характеризует вытянутость эллипса вдоль оси Ох. При с®0, 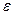 ®0, т.е. оси a и b отличаются между собой не значительно. Если с=0 (
®0, т.е. оси a и b отличаются между собой не значительно. Если с=0 ( от центра.
от центра.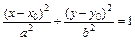
 Если |F1M–F2M|=const=2a, F1F2=2с, и лежат фокусы на Ох так что F1O=OF2, то каноническое уравнение гиперболы запишется в виде:
Если |F1M–F2M|=const=2a, F1F2=2с, и лежат фокусы на Ох так что F1O=OF2, то каноническое уравнение гиперболы запишется в виде:  , где а – действительная полуось, b – мнимая полуось, а b2=c2-a2.
, где а – действительная полуось, b – мнимая полуось, а b2=c2-a2.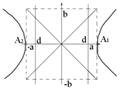 Из уравнения следует, что кривая симметрична относительно осей Ох и Оу.
Из уравнения следует, что кривая симметрична относительно осей Ох и Оу. |a|³0, a>0, a£ |x| < +∞, 0£ |y| +∞.
|a|³0, a>0, a£ |x| < +∞, 0£ |y| +∞.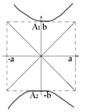 Гипербола имеет также две директрисы. Расстояние от центра до директрисы: d=a/E; E=c/a>1. Гипербола имеет 2 асимптоты. На чертеже это прямы, содержащие диагонали основного прямоугольника, их уравнение: y= ±
Гипербола имеет также две директрисы. Расстояние от центра до директрисы: d=a/E; E=c/a>1. Гипербола имеет 2 асимптоты. На чертеже это прямы, содержащие диагонали основного прямоугольника, их уравнение: y= ±  x.
x. - сопряженная гипербола
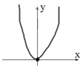
- сопряженная гипербола Парабола – множество точек плоскости, которые равноудалены от данной точки (фокуса) и данной прямой (директрисы). |KM|=|MF|.
Парабола – множество точек плоскости, которые равноудалены от данной точки (фокуса) и данной прямой (директрисы). |KM|=|MF|.
 .
.
 Пусть даны точки: M1(x1; y1;z1), M2(x2;y2;z2), M3(x3; y3; z3), M(x; y; z). Образуем векторы
Пусть даны точки: M1(x1; y1;z1), M2(x2;y2;z2), M3(x3; y3; z3), M(x; y; z). Образуем векторы  .Эти три вектора лежат в одной плоскости, они компланарны, а смешанное произведение компланарных векторов равно 0, т.е.
.Эти три вектора лежат в одной плоскости, они компланарны, а смешанное произведение компланарных векторов равно 0, т.е.  . Если
. Если  ,
,  ,
, 
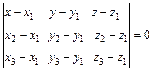 (1)
(1) =(ax; ay; az) и
=(ax; ay; az) и =(bx; by; bz), которые параллельны плоскости,тогда
=(bx; by; bz), которые параллельны плоскости,тогда  (2)
(2) Если плоскость проходит через т. А(x0; y0; z0) и плоскость перпендикулярна вектору
Если плоскость проходит через т. А(x0; y0; z0) и плоскость перпендикулярна вектору  =(a, b, c), а М(x, y, z) произвольная точка плоскости, тогда
=(a, b, c), а М(x, y, z) произвольная точка плоскости, тогда  . В координатной форме имеем
. В координатной форме имеем Уравнение плоскости в отрезках: если плоскость проходит через точки
Уравнение плоскости в отрезках: если плоскость проходит через точки 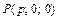 ,
,  и
и  , то применяя уравнение (1) получим
, то применяя уравнение (1) получим 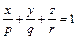 (5)
(5) , а
, а  , то
, то