Функц. распредел. вероятностей непрерывной СВ дает полную вероятностн. хар-ку ее поведения. Однако задание непрерывн. СВ с пом. функц. распредел. не является единственным. Ее можно задать с пом. др. функции, кот. назыв. дифференциальн. функц. распределения или плотностью распредел. вероятностей. Пусть X – несрерывн. СВ с интервальн. функц. распредел. F(x). F(x) непрерывна и дифференцируема в исследуемом интервале. Рассмотрим вер. попадания значения СВ в интервал (x; x+  x). P(x<X<x+
x). P(x<X<x+  x) = F(x+
x) = F(x+  x) – F(x), т.е. вер. равна приращению функц. на этом участке. Определим вер., кот. приходится на единицу длины рассматриваемого участка. Для этого разделим обе части последн. рав-ва на
x) – F(x), т.е. вер. равна приращению функц. на этом участке. Определим вер., кот. приходится на единицу длины рассматриваемого участка. Для этого разделим обе части последн. рав-ва на  x:
x:  =
= 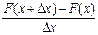 =
=  =
=  =
=  .
.  = f(x). Опред.: Дифференц. функц. распредел. или плотностью распредел. вер. называется 1-ая производная от интегральн. функции распредел. Замеч.: Для хар-ки распредел. вер. дискретн. СВ дифференц. функция распредел. непременима. Основн. св-ва дифференц. функции распредел.: 1) Для
= f(x). Опред.: Дифференц. функц. распредел. или плотностью распредел. вер. называется 1-ая производная от интегральн. функции распредел. Замеч.: Для хар-ки распредел. вер. дискретн. СВ дифференц. функция распредел. непременима. Основн. св-ва дифференц. функции распредел.: 1) Для  f(x) неотрицательна, т.е. f(x)
f(x) неотрицательна, т.е. f(x) 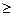 0. Доказ-во: Следует из определения функции плотности F(x) – неубывающ. функция, значит ее производн. неотрицательна, т.е.
0. Доказ-во: Следует из определения функции плотности F(x) – неубывающ. функция, значит ее производн. неотрицательна, т.е.  = f(x)
= f(x) 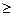 0; 2) Для дифференциальн. функц. распредел. имеет место равенство P(
0; 2) Для дифференциальн. функц. распредел. имеет место равенство P(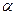 <X<
<X<  ) =
) = 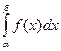 . Доказ-во: Т.к. функц. F(x) явл. первообразной для функц. f(x), то из формулы (
. Доказ-во: Т.к. функц. F(x) явл. первообразной для функц. f(x), то из формулы (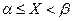 ) = F(
) = F( )-F(
)-F(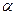 ) и формулы Ньютона-Лейбница вытекает вер. того, что P(
) и формулы Ньютона-Лейбница вытекает вер. того, что P(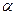 <X<
<X<  ) = F(
) = F( )-F(
)-F(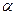 ) =
) = 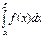 ; 3)Для дифференц. функц. распредел. имеет место рав-во:
; 3)Для дифференц. функц. распредел. имеет место рав-во: 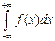 =1. Доказ-во: Согласно определ. несобствен. интеграла по бесконечн. пределам и 3-му св-ву функц. распредел. имеем
=1. Доказ-во: Согласно определ. несобствен. интеграла по бесконечн. пределам и 3-му св-ву функц. распредел. имеем  =
=  +
+  =
= 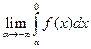 +
+ 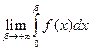 =
= 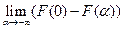 +
+  =
=  +
+  =0+1=1; 4) Для интегральн. и дифференц. функц. распредел. имеет место рав-во: F(x) =
=0+1=1; 4) Для интегральн. и дифференц. функц. распредел. имеет место рав-во: F(x) = 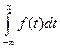 . Доказ-во:
. Доказ-во: 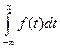 =
= 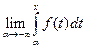 =
= 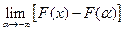 = F(x) -
= F(x) - 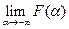 = F(x)-0=F(x). Замеч.: Если СВ Х принимает значение только в некотор. интервале (
= F(x)-0=F(x). Замеч.: Если СВ Х принимает значение только в некотор. интервале ( ), то
), то 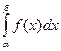 =1.
=1.
25. Матем. ожидание дсв и нсв. Св-ва мат. ожидания.
Мат. ожидание. Возможн. значения СВ могут быть сосредоточены вокруг некотор. центра. Этот центр является некотор. средн. значением, вокруг кот. группируются остальн. значения СВ. Для хар-ки такой особенности распределения СВ служит мат. ожидание, кот. иногда называют центром распределения или ср. значением СВ. Пусть имеется дискретная СВ Х, заданная след. рядом распредел.:
| Х
| x1
| x2
| x3
| …
| xn
|
| Р
| p1
| p2
| p3
| …
| pn
|
Определ.: Мат. ожиданием M(X) дискретн. СВ X назыв. сумма произведений всех возможн. значений случ. величины на соответствующ. вероятности появления этих значений, т.е. M(X)= 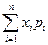 -форм. (1). Если дискретн. СВ принимает бесконечное счетное мн-во значений, то ее мат. ожидание выражается формулой M(X)=
-форм. (1). Если дискретн. СВ принимает бесконечное счетное мн-во значений, то ее мат. ожидание выражается формулой M(X)=  . Причем мат. ожид. в этом случае существует, если ряд в правой части рав-ва сходится абсолютно. Опред.: Мат. ожид. непрерывн. СВ Х, возможн. значения кот. принадлежат отрезку
. Причем мат. ожид. в этом случае существует, если ряд в правой части рав-ва сходится абсолютно. Опред.: Мат. ожид. непрерывн. СВ Х, возможн. значения кот. принадлежат отрезку 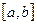 назыв. величина равная M(X)=
назыв. величина равная M(X)=  , где f(x) – функция плотности распредел. непрерывной СВ Х. Если возможн. значения непрерывн. СВ Х принадлежат всей оси ОХ, то M(X)=
, где f(x) – функция плотности распредел. непрерывной СВ Х. Если возможн. значения непрерывн. СВ Х принадлежат всей оси ОХ, то M(X)=  . Здесь предполагается, что несобствен. интеграл сходится абсолютно, т.е. существует. Осн. св-ва мат. ожид.: Опред.: 2 СВ назыв. независимыми, если закон распредел. вероятностей одной из них не зависит от того, какие возможн. значения приняла др. величина. В противн. случае СВ называют зависимыми. Опред.: Неск-ко СВ назыв. взаимно независим., если закон распредел. любой из них не зависит от того, какие значения приняли какие-л. другие из оставшихся величин. 1) Мат. ожид. постоянной величины равно самой постоянной, т.е. M(C)=C. Доказ-во: Постоян. C можно рассматривать как дискретную СВ, кот. принимает знач. C с вероятностью =1. Тогда по формуле (1): M(C) =C
. Здесь предполагается, что несобствен. интеграл сходится абсолютно, т.е. существует. Осн. св-ва мат. ожид.: Опред.: 2 СВ назыв. независимыми, если закон распредел. вероятностей одной из них не зависит от того, какие возможн. значения приняла др. величина. В противн. случае СВ называют зависимыми. Опред.: Неск-ко СВ назыв. взаимно независим., если закон распредел. любой из них не зависит от того, какие значения приняли какие-л. другие из оставшихся величин. 1) Мат. ожид. постоянной величины равно самой постоянной, т.е. M(C)=C. Доказ-во: Постоян. C можно рассматривать как дискретную СВ, кот. принимает знач. C с вероятностью =1. Тогда по формуле (1): M(C) =C  p=C
p=C  1=C; 2) Постоян. множитель можно выносить за знак мат. ожид., т.е. M(kX)=kM(X). Доказ-во: Возможн. знач., кот. принимает СВ kX – это kx1, kx2,…,kxn. Им соответствуют вероятн. p1, p2,…,pn. Тогда M(kX)=
1=C; 2) Постоян. множитель можно выносить за знак мат. ожид., т.е. M(kX)=kM(X). Доказ-во: Возможн. знач., кот. принимает СВ kX – это kx1, kx2,…,kxn. Им соответствуют вероятн. p1, p2,…,pn. Тогда M(kX)=  =
=  = kM(X); 3) Мат. ожид. алгебраич. суммы 2-ух СВ X и Y равно алгебраич. сумме их мат. ожиданий, т.е. M(X
= kM(X); 3) Мат. ожид. алгебраич. суммы 2-ух СВ X и Y равно алгебраич. сумме их мат. ожиданий, т.е. M(X  Y)=M(X)
Y)=M(X)  M(Y). Доказ-во: Пусть X и Y – дискретн. СВ, имеющие след. ряды распред.:
M(Y). Доказ-во: Пусть X и Y – дискретн. СВ, имеющие след. ряды распред.:
| Х
| x1
| x2
| x3
| …
| xn
|
| Р
| p1
| p2
| p3
| …
| pn
|
(Тоже самое для Y, только вместо p – q и в конце ym и qm). Пусть X и Y – независим. СВ. Найдем вер. появления значения  , соответствующ. значению СВ
, соответствующ. значению СВ  . Для появл. указан. значения необходимо, чтобы с вер.
. Для появл. указан. значения необходимо, чтобы с вер. 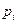 появилось значение
появилось значение  СВ Х, а с вер.
СВ Х, а с вер.  - значение СВ Y
- значение СВ Y 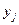 . Значит вер. появл. значения
. Значит вер. появл. значения  =
= 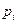
 . Ряд распред. дискретн. СВ
. Ряд распред. дискретн. СВ  будет иметь вид:
будет иметь вид:
Тогда M(X  Y)=
Y)= 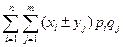 =
= 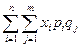

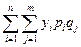 =
= 

 = M(X)
= M(X)  M(Y); 4) Мат. ожид. произведения 2-ух независим. СВ X и Y равно произведению их мат. ожиданий, т.е. M(XY)=M(X)
M(Y); 4) Мат. ожид. произведения 2-ух независим. СВ X и Y равно произведению их мат. ожиданий, т.е. M(XY)=M(X)  M(Y). Доказ-во: Пусть дискретн. СВ X и Y заданы рядами распред., приведенными при доказ-ве св-ва 3. Ряд распред. СВ XY для независим. СВ имеет вид: (такой же как и предыдущий, только x1
M(Y). Доказ-во: Пусть дискретн. СВ X и Y заданы рядами распред., приведенными при доказ-ве св-ва 3. Ряд распред. СВ XY для независим. СВ имеет вид: (такой же как и предыдущий, только x1  y1 и т.д.). Тогда мат. ожид. M(XY)=
y1 и т.д.). Тогда мат. ожид. M(XY)=  =
= 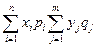 = M(X)
= M(X)  M(Y). Замеч.: Св-ва доказанные для дискретн. СВ справедливы и для непрерывн. СВ; 5) Мат. ожид. отклонения СВ от ее мат. ожид. равно 0, т.е. M(X – M(X))=0. Доказ-во: Используя св-ва 3 и 1 и учитывая, что мат. ожид. – величина постоянная, получаем, что M(X – M(X))= M(X) – M(M(X)) = M(X) – M(X) =0. Замеч.: Разность X – M(X) показывает, насколько знач. СВ отклонилось от мат. ожид. Эту величину назыв. отклонением СВ Х от ее мат. ожидания.
M(Y). Замеч.: Св-ва доказанные для дискретн. СВ справедливы и для непрерывн. СВ; 5) Мат. ожид. отклонения СВ от ее мат. ожид. равно 0, т.е. M(X – M(X))=0. Доказ-во: Используя св-ва 3 и 1 и учитывая, что мат. ожид. – величина постоянная, получаем, что M(X – M(X))= M(X) – M(M(X)) = M(X) – M(X) =0. Замеч.: Разность X – M(X) показывает, насколько знач. СВ отклонилось от мат. ожид. Эту величину назыв. отклонением СВ Х от ее мат. ожидания.
26. Дисперсия дсв и нсв. Св-ва дисперсии.
Дисперсией D(X) СВ называют матем. ожидание квадрата ее отклонения от мат. ожидания, т.е. D(X)=M(X-M(X))2. Выбор дисперсии, определяемой по предыдущ. формуле в кач-ве хар-ки рассеивания значения СВ оправдывается тем, что дисперсия обладает св-вом минимальности. Это означает, что дисп. равна 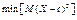 . Если X – это дискретн. СВ, то D(X)=
. Если X – это дискретн. СВ, то D(X)=  . Если X – это непрерывн. СВ, принимающ. значения отрезка [a,b], то D(X)=
. Если X – это непрерывн. СВ, принимающ. значения отрезка [a,b], то D(X)=  f(x)dx, где f(x) – функция плотности распределения непрерывн. СВ X. D(X) имеет размерность квадрата СВ, что не всегда удобно, поэтому в кач-ве показателя рассеивания используют также величину
f(x)dx, где f(x) – функция плотности распределения непрерывн. СВ X. D(X) имеет размерность квадрата СВ, что не всегда удобно, поэтому в кач-ве показателя рассеивания используют также величину 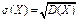 . Ее называют средним квадратич. отклонением. Основн. св-ва дисперсии: 1) Дисперс. алгебраич. суммы 2-ух независим. СВ X и Y равна сумме дисперсий этих величин, т.е. D(X
. Ее называют средним квадратич. отклонением. Основн. св-ва дисперсии: 1) Дисперс. алгебраич. суммы 2-ух независим. СВ X и Y равна сумме дисперсий этих величин, т.е. D(X  Y)=D(X)+D(Y). Доказ-во: D(X
Y)=D(X)+D(Y). Доказ-во: D(X  Y)= M[(X
Y)= M[(X  Y) – M(X
Y) – M(X  Y)]2 = M((X
Y)]2 = M((X  Y) – (M(X)
Y) – (M(X)  M(Y)))2 = M((X – M(X)
M(Y)))2 = M((X – M(X)  (Y – M(Y)))2 = M[(X – M(X))2
(Y – M(Y)))2 = M[(X – M(X))2  2(X – M(X))(Y – M(Y)) + (Y – M(Y))]2 = M(X – M(X))2
2(X – M(X))(Y – M(Y)) + (Y – M(Y))]2 = M(X – M(X))2  2M(X – M(X))M(Y – M(Y)) + M(Y – M(Y))2 = D(X) + 0 + D(Y) = D(X)+D(Y); 2) Дисперсия постоян. величины равна 0, т.е. D(C)=0. Доказ-во: Т.к. M(C)=C, то D(C)= M(C – M(C))2 = M(C – C)2 = M(0) = 0; 3) Постоян. множитель С можно выносить за знак дисперсии, возводя его в квадрат, т.е. D(CX)= C2D(X). Доказ-во: D(C)= M(CX – M(CX))2 = M(CX – CM(X))2 = M(C(X – M(X))2) = M(C2(X – M(X))2) = M(C2)M(X – M(X))2 = C2D(X); 4) Дисперсия СВ Х равна разности между мат. ожиданием квадрата СВ и квадратом ее мат. ожидания, т.е. D(X) = M(X2) – (M(X))2. Доказ-во: По определ. дисперсии D(X) = M(X – M(X))2 = M(X2 – 2X M(X) + (M(X))2) = M(X2) – M(2X M(X)) + M(M(X))2 = M(X2) – 2M(X) M(X) + (M(X))2 = M(X2) – (M(X))2. Замечание: При решении практич. задач для вычисления удобнее использовать формулу св-ва (4). Для дискретн. СВ эта формула будет иметь вид: D(X) =
2M(X – M(X))M(Y – M(Y)) + M(Y – M(Y))2 = D(X) + 0 + D(Y) = D(X)+D(Y); 2) Дисперсия постоян. величины равна 0, т.е. D(C)=0. Доказ-во: Т.к. M(C)=C, то D(C)= M(C – M(C))2 = M(C – C)2 = M(0) = 0; 3) Постоян. множитель С можно выносить за знак дисперсии, возводя его в квадрат, т.е. D(CX)= C2D(X). Доказ-во: D(C)= M(CX – M(CX))2 = M(CX – CM(X))2 = M(C(X – M(X))2) = M(C2(X – M(X))2) = M(C2)M(X – M(X))2 = C2D(X); 4) Дисперсия СВ Х равна разности между мат. ожиданием квадрата СВ и квадратом ее мат. ожидания, т.е. D(X) = M(X2) – (M(X))2. Доказ-во: По определ. дисперсии D(X) = M(X – M(X))2 = M(X2 – 2X M(X) + (M(X))2) = M(X2) – M(2X M(X)) + M(M(X))2 = M(X2) – 2M(X) M(X) + (M(X))2 = M(X2) – (M(X))2. Замечание: При решении практич. задач для вычисления удобнее использовать формулу св-ва (4). Для дискретн. СВ эта формула будет иметь вид: D(X) = 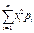 - (M(X))2. Для непрерывн. СВ: D(X) =
- (M(X))2. Для непрерывн. СВ: D(X) =  - (M(X))2.
- (M(X))2.

 x). P(x<X<x+
x). P(x<X<x+  =
= 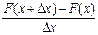 =
=  =
=  =
=  .
.  f(x) неотрицательна, т.е. f(x)
f(x) неотрицательна, т.е. f(x) 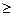 0. Доказ-во: Следует из определения функции плотности F(x) – неубывающ. функция, значит ее производн. неотрицательна, т.е.
0. Доказ-во: Следует из определения функции плотности F(x) – неубывающ. функция, значит ее производн. неотрицательна, т.е. 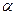 <X<
<X<  ) =
) = 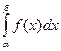 . Доказ-во: Т.к. функц. F(x) явл. первообразной для функц. f(x), то из формулы (
. Доказ-во: Т.к. функц. F(x) явл. первообразной для функц. f(x), то из формулы (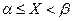 ) = F(
) = F(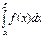 ; 3)Для дифференц. функц. распредел. имеет место рав-во:
; 3)Для дифференц. функц. распредел. имеет место рав-во: 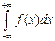 =1. Доказ-во: Согласно определ. несобствен. интеграла по бесконечн. пределам и 3-му св-ву функц. распредел. имеем
=1. Доказ-во: Согласно определ. несобствен. интеграла по бесконечн. пределам и 3-му св-ву функц. распредел. имеем  =
=  +
+  =
= 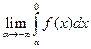 +
+ 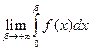 =
= 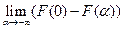 +
+  =
=  +
+  =0+1=1; 4) Для интегральн. и дифференц. функц. распредел. имеет место рав-во: F(x) =
=0+1=1; 4) Для интегральн. и дифференц. функц. распредел. имеет место рав-во: F(x) = 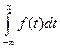 . Доказ-во:
. Доказ-во: 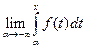 =
= 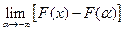 = F(x) -
= F(x) - 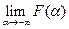 = F(x)-0=F(x). Замеч.: Если СВ Х принимает значение только в некотор. интервале (
= F(x)-0=F(x). Замеч.: Если СВ Х принимает значение только в некотор. интервале ( ), то
), то 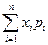 -форм. (1). Если дискретн. СВ принимает бесконечное счетное мн-во значений, то ее мат. ожидание выражается формулой M(X)=
-форм. (1). Если дискретн. СВ принимает бесконечное счетное мн-во значений, то ее мат. ожидание выражается формулой M(X)=  . Причем мат. ожид. в этом случае существует, если ряд в правой части рав-ва сходится абсолютно. Опред.: Мат. ожид. непрерывн. СВ Х, возможн. значения кот. принадлежат отрезку
. Причем мат. ожид. в этом случае существует, если ряд в правой части рав-ва сходится абсолютно. Опред.: Мат. ожид. непрерывн. СВ Х, возможн. значения кот. принадлежат отрезку 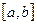 назыв. величина равная M(X)=
назыв. величина равная M(X)=  , где f(x) – функция плотности распредел. непрерывной СВ Х. Если возможн. значения непрерывн. СВ Х принадлежат всей оси ОХ, то M(X)=
, где f(x) – функция плотности распредел. непрерывной СВ Х. Если возможн. значения непрерывн. СВ Х принадлежат всей оси ОХ, то M(X)=  . Здесь предполагается, что несобствен. интеграл сходится абсолютно, т.е. существует. Осн. св-ва мат. ожид.: Опред.: 2 СВ назыв. независимыми, если закон распредел. вероятностей одной из них не зависит от того, какие возможн. значения приняла др. величина. В противн. случае СВ называют зависимыми. Опред.: Неск-ко СВ назыв. взаимно независим., если закон распредел. любой из них не зависит от того, какие значения приняли какие-л. другие из оставшихся величин. 1) Мат. ожид. постоянной величины равно самой постоянной, т.е. M(C)=C. Доказ-во: Постоян. C можно рассматривать как дискретную СВ, кот. принимает знач. C с вероятностью =1. Тогда по формуле (1): M(C) =C
. Здесь предполагается, что несобствен. интеграл сходится абсолютно, т.е. существует. Осн. св-ва мат. ожид.: Опред.: 2 СВ назыв. независимыми, если закон распредел. вероятностей одной из них не зависит от того, какие возможн. значения приняла др. величина. В противн. случае СВ называют зависимыми. Опред.: Неск-ко СВ назыв. взаимно независим., если закон распредел. любой из них не зависит от того, какие значения приняли какие-л. другие из оставшихся величин. 1) Мат. ожид. постоянной величины равно самой постоянной, т.е. M(C)=C. Доказ-во: Постоян. C можно рассматривать как дискретную СВ, кот. принимает знач. C с вероятностью =1. Тогда по формуле (1): M(C) =C  p=C
p=C  =
=  = kM(X); 3) Мат. ожид. алгебраич. суммы 2-ух СВ X и Y равно алгебраич. сумме их мат. ожиданий, т.е. M(X
= kM(X); 3) Мат. ожид. алгебраич. суммы 2-ух СВ X и Y равно алгебраич. сумме их мат. ожиданий, т.е. M(X  Y)=M(X)
Y)=M(X)  , соответствующ. значению СВ
, соответствующ. значению СВ  . Для появл. указан. значения необходимо, чтобы с вер.
. Для появл. указан. значения необходимо, чтобы с вер. 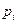 появилось значение
появилось значение  СВ Х, а с вер.
СВ Х, а с вер.  - значение СВ Y
- значение СВ Y 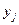 . Значит вер. появл. значения
. Значит вер. появл. значения 


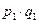


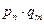
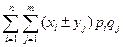 =
= 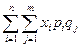
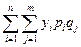 =
= 
 = M(X)
= M(X)  =
= 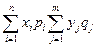 = M(X)
= M(X) 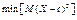 . Если X – это дискретн. СВ, то D(X)=
. Если X – это дискретн. СВ, то D(X)=  . Если X – это непрерывн. СВ, принимающ. значения отрезка [a,b], то D(X)=
. Если X – это непрерывн. СВ, принимающ. значения отрезка [a,b], то D(X)=  f(x)dx, где f(x) – функция плотности распределения непрерывн. СВ X. D(X) имеет размерность квадрата СВ, что не всегда удобно, поэтому в кач-ве показателя рассеивания используют также величину
f(x)dx, где f(x) – функция плотности распределения непрерывн. СВ X. D(X) имеет размерность квадрата СВ, что не всегда удобно, поэтому в кач-ве показателя рассеивания используют также величину 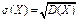 . Ее называют средним квадратич. отклонением. Основн. св-ва дисперсии: 1) Дисперс. алгебраич. суммы 2-ух независим. СВ X и Y равна сумме дисперсий этих величин, т.е. D(X
. Ее называют средним квадратич. отклонением. Основн. св-ва дисперсии: 1) Дисперс. алгебраич. суммы 2-ух независим. СВ X и Y равна сумме дисперсий этих величин, т.е. D(X 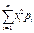 - (M(X))2. Для непрерывн. СВ: D(X) =
- (M(X))2. Для непрерывн. СВ: D(X) =  - (M(X))2.
- (M(X))2.


