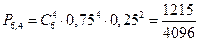Вероятностное пространство.Говорят, что имеется вероятностная (математическая) модель случайного опыта, если построены: 1) пространство элементарных событий Е 2) поле событий К 3) распределение вероятностей на поле событий К, т.е. для каждого события А из поля событий К задана вероятность Р (А) Тройка объектов (Е, К, Р) называется вероятностным пространством (моделью) данного случайного опыта. Если Е – дискретное, то (Е, К, Р) называется дискретным. Если Е – непрерывное, то (Е, К, Р) называется непрерывным.
§6. Классическая вероятностная модель.
Вероятностная модель называется классической, если выполнены следующие 2 условия: 1) пространство элементарных событий – дискретное конечное, состоит из n элементарных событий Е ={ e1, e2, …, en } 2)
Вероятностное пространство определяется так: для заданного пространства Е поле событий К - есть множество всех подмножеств из Е, а вероятности Р (А) для любого события А из К выражаются через вероятности элементарных событий. Пусть По аксиоме 3:
§7. Геометрические вероятности.
Классическая модель: дискретная вероятностная модель Геометрическая модель: непрерывная вероятностная модель (Е, К, Р) Е – непрерывное пространство, множество точек области на плоскости К ={ A } А из Е: А – длина; А – площадь; А – объём
Наудачу бросается точка, наблюдается событие: попадание точки в область А. «Наудачу» означает: вероятность события А зависит от площади А, не зависит от её формы и положения Е.
§8. Теорема о сложении вероятностей.
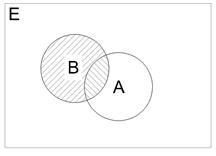
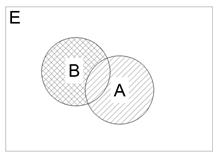
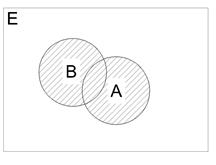
(Не путать с аксиомой о сложении вероятностей). Теорема. Задано вероятностное пространство (Е, К, Р), есть события А, В
По аксиоме 3:
Вычитая из 1-го равенства 2-е получим ч.т.д. Замечание: из аксиомы 3 следует, что если события
§9. Условные вероятности.
Пример. Три раза бросается монета. Результат: цифра или герб.
n =8 A – герб выпал один раз;
Пусть в результате опыта произошло событие В. Число выпавших гербов – нечётно.
Тогда, если В произошло, Рассмотрим более общую ситуацию: пусть некоторому случайному опыту соответствует классическая вероятностная модель.
r элементарных событий входит и в А и в В. Найдём вероятность события А при условии, что произошло В. Если В произошло, то его вероятность равна 1, то Событие А происходит, если происходит элементарное событие, принадлежащее пересечению, их всего r.
Определение: пусть задано вероятностное пространство (Е, К, Р); А, В – события. Если Теорема умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из событий на условную вероятностью другого, вычисленную при условии, что событие первое имело место. Вероятность произведения n событий.
Пример. В урне 12 шаров: 5 белых, 7 чёрных. 2 лица один за другим вынимают по одному шару. Найти вероятность того, что оба шара белые. А – белый шар у Пети В – белый шар у Маши
Пример. Вероятность попадания в цель при стрельбе из 1-го и 2-го орудия равны:
Найти вероятность попадания при одном залпе хотя бы одним из орудий. А – попадание из 1-го орудия В – попадание из 2-го орудия А + В – попадание хотя бы из одного
Зависимые и независимые события. Два события А и В называются независимыми, если вероятность их произведения равна произведению их вероятностей.
Свойства независимых событий: 1 ̊. Если P (A)>0, то независимость А и В эквивалентна равенству P (A / B)= P (A). Вероятность А не меняется, если В произошло.
Из последнего равенства получаем:
Пример. Опыт: 2 раза бросается монета. События: А – герб при 1-м бросании В – выпадение цифры при 2-м бросании
А и В – независимые?
§10. Формула полной вероятности. Формулы Байеса.
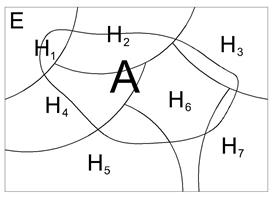
Формула полной вероятности. Пусть (Е, К, Р) – модель некоторого случайного опыта. Н1, Н2, …, Нn – полная группа. 1) 2)
Hi – гипотеза
Доказательство: т.к. Hi – попарно несовместные, Пример. Имеются 3 одинаковых урны. Состав: 1-я – 2 белых, 1 чёрный; 2-я – 3 белых, 1 чёрный; 3-я – 2 белых, 2 чёрных. Наудачу выбирается урна; из неё вынимается шар. Найти вероятность того, что шар – белый. Гипотезы: Hi – выбрана i -я урна, i =1,2,3.
А – шар белый
Формулы Байеса. Если вероятности гипотез до опыта известны, то их называют априорные вероятности гипотез. Пусть известно, что событие А произошло. Вероятность всех гипотез изменяется. Вероятности гипотез после того, как событие А произошло – апостериорные вероятности. Пусть в условиях предыдущего примера известно, что вытащен белый шар. Найти вероятность того, что шар вытащен из второй урны.
§11. Последовательности независимых испытаний. Схема Бернулли.
До сих пор мы рассматривали один опыт, для него строили вероятностную модель (Е, К, Р). Теперь будем рассматривать несколько опытов, причём каждый имеет 2 исхода ( Будем рассматривать составной опыт, составленный из таких n независимых опытов. Вероятностная модель такого составного опыта называется схемой Бернулли. Построим вероятностное пространство составного опыта. (Е, К, Р) 1. E, e – результат совместного (одновременного) рассмотрения исходов n испытаний (опытов). Элементарные события будем записывать в виде последовательности букв У и Н. е =(УННУ … У) (*) Причём, если в опыте с номером k имел место успех, то на k -м месте ставим У, неудача – Н.
Е – множество всех конечных последовательностей вида (*). Е – конечное
2. K ={ A } 3.
Если m раз – успех
Всего таких е, которые составляют событие А – это число способов расставить букву У на m местах среди n мест, т.е. это число сочетаний из m по n (
Вероятность того, что расход электроэнергии в течение суток не превысит установленной нормы – 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит установленной нормы. У – расход нормы не превысит нормы Н – норма будет превышена Р (У)=0,75; Р (Н)=0,25 n =6
|

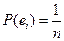 - вероятности всех элементарных событий равны
- вероятности всех элементарных событий равны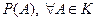


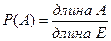 ;
;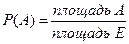 ;
;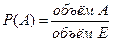 .
. Эти вероятностные пространства служат моделью задач такого типа:
Эти вероятностные пространства служат моделью задач такого типа: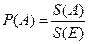
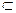 Е.
Е.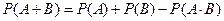
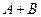
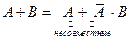
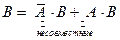
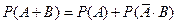
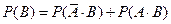
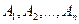 составляют полную группу,
составляют полную группу, 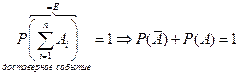
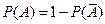
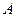 и
и 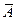 - полная группа
- полная группа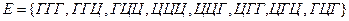
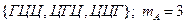
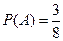
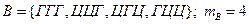
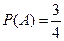 .
.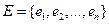 , n элементарных событий
, n элементарных событий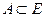
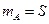
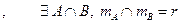
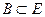
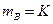
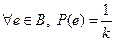 .
.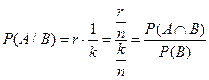
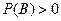 , то условной вероятностью события А при условии, что событие В произошло, называется отношение
, то условной вероятностью события А при условии, что событие В произошло, называется отношение 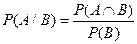
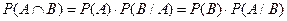
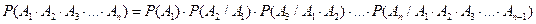
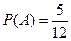 ;
; 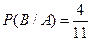
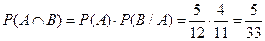
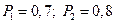 .
.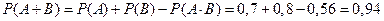
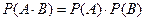
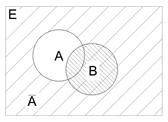 2 ̊. Если А и В – независимые события, то
2 ̊. Если А и В – независимые события, то 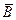 - независимые.
- независимые.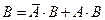
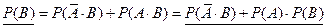
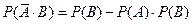
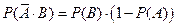

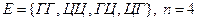
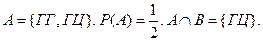
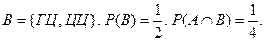
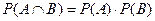 .
.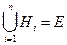
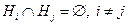
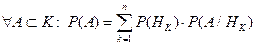
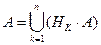 , по аксиоме 3
, по аксиоме 3 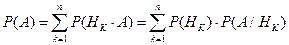 .
.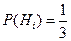 .
.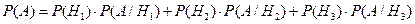
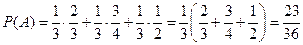 .
.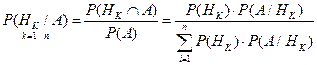
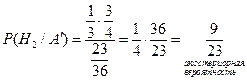
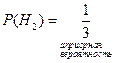
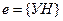 (успех, неудача).
(успех, неудача). 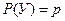 ;
; 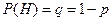 .
.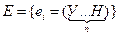
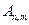 - означающее, что в составном опыте m из n раз имел место успех.
- означающее, что в составном опыте m из n раз имел место успех.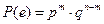
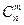 ).
).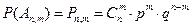 - формула Бернулли.
- формула Бернулли.