Методы математического описания САУ. Передаточная функцияСтатическая модель описывает поведение системы в равновесном состоянии:
В общем случае функция (*) нелинейна, поэтому ее линеаризуют, раскладывая в ряд Тейлора в окрестностях рабочей точки:
Оставляя только линейные члены ряда можно записать:
где k - коэффициент передачи объекта. Если выходная величина объекта зависит от нескольких входных воздействий, то при линеаризации по методу малых приращений следует определять частные производные по всем воздействиям, а приращение выходной величины является суммой частных приращений входных воздействий, т.е:
где Δx 1, Δx n – приращения вх.воздействий. Динамические хар-ки. Динамическая модель описывает изменение входных и выходных величин во времени. Если объект имеет один выход, то динамическая модель в общем случае имеет вид:
где y(t), x(t) – выходная и входная величины; a i и b i, – постоянные коэффициенты; n – порядок уравнения, при этом n ≥ m – условие физической реализуемости элемента.Если входных величин несколько – то они и их производные записываются в правой части уравнения.Если объект имеет k выходов, то его динамика описывается системой k дифуравнений. Динамические характеристики рассматривают при трех стандартных входных воздействиях: - единичном ступенчатом – 1(t),- единичном импульсном – δ(t),- периодическом (синусоидальном).В первых двух случаях полученные характеристики называются временными, в третьем – частотными. По временным характеристикам определяют качество регулирования. Ур-я динамики реш. классич. или операторным методами. Классический метод примен. для реш. линейных ур-ний, если их порядок не превышает трех, а правая часть выражается простой функцией – константой или синусоидой. Общее решение ур-я динамики (неоднородное дифуравнение) это сумма общего решения соответств. однородного ур-я и частного решения неоднородного ур-я. Однородное ур-е хар-ует поведение системы, предоставленной самой себе, после снятия внешних возмущений. Его наз. ур-ем свобод. движения системы:
Частное решение неоднородного уравнения описывает поведение системы, определяемое свойствами системы и видом воздействия, и называется вынужденным.Тогда:
Решением уравнения свободного движения является:
где p i – корни характеристического уравнения:
A i – постоянные интегрирования, определяемые из начальных условий. Операторный метод реш. ур-й динамики предусматр.т:- приведение дифура-й к операторной форме, с исп. преобразование Лапласа с учетом заданных начальных условий; - решение полученного ур-я относит. искомой величины, записанной в операторной форме, используя в случае необходимости свойства преобразования;- нахождение решения исходного уравнения динамики в обычной форме, применяя операцию обратного преобразования Лапласа. Прямым преобразованием Лапласа функции f(t) действительного переменного t называется функция F(p) комплексного аргумента p = α + iω; определяемая по формуле:
где L – символ операции прямого преобразования Лапласа.Функцию f(t), называют оригиналом, а функцию F(p),– изображением.Уравнение динамики системы в операторной форме всегда проще исходного дифференциального уравнения. При этом оно учитывает начальные условия и отражает физическую картину переходного процесса в системе.Для отыскания оригинала по соответствующему изображению F(p) надо провести операцию обратного преобразования Лапласа, которая обозначается символом L -1:
Вычисление интеграла затруднительно и поэтому решения для распространенных случаев приводятся в таблице.Если изображения нет в таблице, то его необходимо привести к удобной для решения форме. Часто изображение F(p) можно выразить в виде дробно-рациональной функции от р:
если один из корней знаменателя равен 0, то оригинал может быть найден по формуле:
где р i – ненулевые корни знаменателя.Выраженное в операторной форме ур-е динамики позв. найти передаточную функцию системы:
|

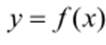 ,(*)где у – выходная величина, х – входная величина.
,(*)где у – выходная величина, х – входная величина.
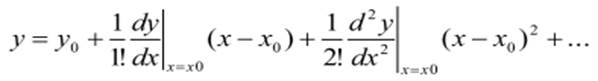
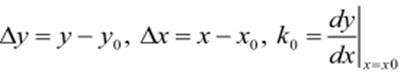
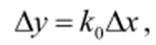
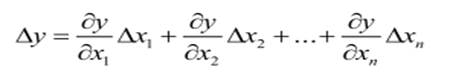

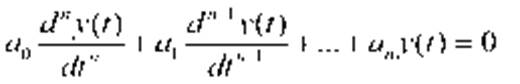 .
.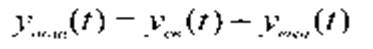 .
.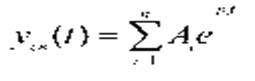
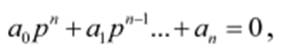
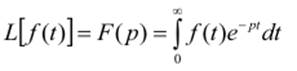
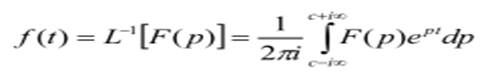
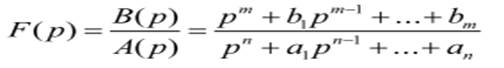 .
.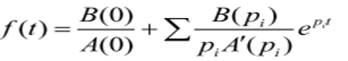 ,
,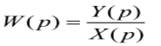 .где Y(p) и X(p) – изображения по Лапласу выходной и входной величин при нулевых начал. усл. соответст.С пом. передаточных функций можно упростить описание динамики как АСР в целом, так и их элементов.
.где Y(p) и X(p) – изображения по Лапласу выходной и входной величин при нулевых начал. усл. соответст.С пом. передаточных функций можно упростить описание динамики как АСР в целом, так и их элементов.


