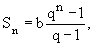А. Простой и сложный процентПусть некто внес в банк сегодня 100 руб. под 50% годовых. Очевидно, что через год [Под "годом" здесь и далее понимается не обязательно календарный год, но любой временной период, на который начисляется процент.] на счете будет сумма вклада плюс процент на нее. Последний исчисляется умножением процентной ставки на величину вклада (100×0,5). Итого получаем: 100 + 0,5×100 = 100(1 + 0,5) = 150 Решим задачу в общем виде, обозначив начальную сумму вклада – K0, процентную ставку – i и сумму через год – K1. Тогда имеем: K1 = K0 + iK0 = K0(1 + i) Если начиная со второго года банк начисляет процент только на первоначально вложенную сумму, то такой процент называется простым. В этом случае, вложив 100 руб. под 50% годовых, мы через два года получаем на счете 200 руб. Расчет таков: 100 + 0,5×100 + 0,5×100 = 100(1 + 2×0,5) = 200 Обозначив сумму, которая будет на счете через два года – K2, получаем в общем виде: K2 = K0 + iK0 + iK0 = K0(1 + 2i). Следовательно, через n лет имеем на счете: Kn= K0(1 + ni) Если, начиная со второго года, банк начисляет процент на всю накопленную ранее сумму, то такой процент называется сложным. Вернемся к нашему условному примеру с вложением 100 руб. под 50% годовых. Как уже было установлено, мы имеем на счете через год: K1 = 100(1+0,5) = 150. В следующем году процент начисляется уже на 150 руб. Следовательно, через два года на счете будет: K2 = 150(1 + 0,5) = 100(1 + 0,5)(1 + 0,5) = 100(1 + 0,5)2 = 225 В общем виде получаем: K2 = K0(1 + i)2. Таким образом, через n лет сумма на счете (Kn) будет: Kn = K0(1 + i)n Усложним модель. До этого предполагалось, что деньги вносятся на счет один единственный раз. Теперь допустим, что некто ежегодно вносит в банк одну и ту же сумму (K руб.) под i% годовых (начисляется сложный процент). В качестве примера предположим, что вы решили копить деньги к отпуску, для чего первого числа каждого месяца вкладываете в банк K руб. Банк платит по вкладам i% в месяц. Первый взнос сделан 1 сентября, второй – 1 октября и т.д. вплоть до 1 июля, когда вы больше ничего не вкладываете, а снимаете деньги со счета и уезжаете отдыхать. Итак, подсчитаем: Первого сентября на счет положено K руб.:
Первого октября эта сумма превратится в K(1+i), но вы докладываете еще K руб., и всего на счете оказывается K(1+i) + K руб.:
К первому ноября сентябрьские деньги пролежали на счете два месяца, превратившись в K(1+i)2, октябрьские K руб., будучи на счете один месяц, превратились в K(1+i), кроме того, K руб. вносятся дополнительно. Всего, таким образом, вы имеете на счете K(1+i)2 + K(1+i) + K руб.:
Декабрь, январь и т.д. пропустим. Наступает 1 июля. К этому времени сентябрьские деньги пробыли на счете 10 месяцев и превратились в K(1+i)10, соответственно деньги, внесенные 1 октября, стали K(1+i)9. И т. д. Последний раз K руб. были вложены 1 июня, т.е. превратились в K(1+i) руб. Поэтому вы закрываете счет, имея K(1+i)10 + K(1+i)9 +...+ K(1+i) руб.:
Рассмотренный пример – частный случай. Если же подобная операция продолжается n лет (временных периодов), то в конце срока сумма на счете (Kn) будет: Kn = K(1 + i) + K(1 + i)2 +...+ K(1 + i)n Перед нами геометрическая прогрессия, сумма членов которой (Sn) исчисляется по формуле:
где b – первый член прогрессии [в нашем примере: K(1+i)], q – знаменатель (общий множитель) прогрессии (у нас: 1+i), а n – число членов прогрессии. Следовательно, в нашем случае:
Все приведенные расчеты называются нахождением будущей стоимости (FV). Следовательно: Kn = FVn.
|