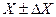Погрешности измерений. Любое измерение производится с какой-то степенью точностиЛюбое измерение производится с какой-то степенью точности. Это связано с несовершенством измерительных приборов, методики измерений, несовершенством органов человеческих чувств и т.п. При этом измеренная величина всегда отличается от ее истинного значения. Другими словами, всякое измерение характеризуется наличием ошибок - погрешностей. Во многих случаях погрешности оказываются весьма значительными. Поэтому в задачу экспериментатора помимо измерения искомой величины в обязательном порядке входит оценка погрешности полученного результата. Без такой оценки результат опыта не имеет, как правило, практической ценности. Обычно значение измеренной величины X записывают в следующем виде:
где ΔХ - абсолютная погрешность измерения, характеризующая отклонение измеренного значения данной величины от ее истинного значения. При этом, поскольку истинное значение остается неизвестным (т.к. в принципе нельзя осуществить абсолютно точное измерение), можно дать лить приближенную оценку абсолютной погрешности. Поскольку причины возникновения ошибок могут быть самыми разными, необходимо классифицировать погрешности, возникающие в ходе экспериментов. Только в этом случае возможна правильная опенка погрешности полученного результата, так как от типа погрешностей зависит и способ их вычисления. Погрешности подразделяются на случайные и систематические. Систематической погрешностью называют составляющую погрешности измерения, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины. Случайной погрешностью называют составляющую погрешности измерения, изменяющуюся случайным образом при повторных измерениях одной и той же величины. Выделяют также погрешности приборов, которые могут иметь как систематический, так и случайный характер. Рассмотрим некоторые причины, вызывающие появление систематических и случайных погрешностей. Систематическая погрешность может быть связана с неисправностями измерительных приборов, неточностью их регулировки, несоблюдением условий их эксплуатации и т.п. Такие погрешности возникают, например, при не совсем горизонтальном положении некоторых приборов или при использовании стрелочного прибора, у которого стрелка до начала измерений не была установлена на нуль. Заметим, что указанные погрешности не относятся к разряду приборных, которые характеризуют вполне исправные и правильно эксплуатируемые инструменты. Причина возникновения систематической погрешности может заключаться и в самой методике измерений. Так, например, определяя плотность твердого тела по измерениям его массы и объема, можно допустить ошибку, если внутри исследуемого тела имеются пустоты в виде пузырьков воздуха. В этом случае устранить ошибку можно только изменив метод измерений. Случайные погрешности связаны с некоторыми случайными факторами, влияющими на точность измерений. Они могут зависеть от условий, в которых производится эксперимент. Например, обычный сквозняк в лабораторном помещении может случайным образом сказаться на измерениях температуры. Измерения промежутков времени запускаемым вручную секундомером также приводит к возникновению случайных погрешностей, связанных со случайным изменением времени реакции экспериментатора. Появление случайных погрешностей может быть связано со спецификой измеряемой величины. Если, например, измерять штангенциркулем размеры неточно изготовленной детали, то полученные результаты будут случайным образом зависеть от положения измерительного прибора. Еще один пример – неточность отсчета по шкале стрелочного прибора, связанная со случайным Мнением положения глаз экспериментатора относительно прибора. Основным способом уменьшения случайных погрешностей является многократное измерение одной и той же физической величины. Заметим, однако, что максимально возможная точность измерения определяется теми приборами, которые используются в эксперименте. Поэтому уменьшение случайной погрешности путем увеличения числа опытов имеет смысл до тех пор, пока ее величина не станет явно меньше величины погрешности прибора. Погрешности приборов связаны с несовершенством любого измерительного инструмента. Если значение измеряемой величины определяется по шкале инструмента, абсолютная погрешность прибора считается, как правило, равной половине цены деления шкалы (например, линейки) или цене деления шкалы, если стрелка прибора перемещается скачком (секундомер) приборов, снабженных нониусом, погрешность можно считать равной точности нониуса. Погрешности электроизмерительных приборов определяют по их классу точности, который указывается на шкале.
|