Нахождение оптимума линейной функцииПример: Решим симплексным методом задачу: F=2x1 + 3х2 à max х1 + 3х2 <= 18 2х1 + х2 <= 16 х2 <= 5 3x1 <= 21
х1 + 3х2 + х3 = 18 2х1 + х2 + х4 = 16 х2 + х5 = 5 3x1 + х6 = 21 Для нахождения первоначального БР разобъем на основные (базисные) и неосновные (свободные). Т.к. определитель при переменных х3 – х6 не равен 0, то на первом шаге – основные. Не обязательно составлять определитель на первом шаге. Следующее правило: В качестве основных переменных на первом шаге следует выбрать (если возможно) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных. Если выбранные переменные имеют те же знаки, что и соответствующие им свободные члены, то полученное БР будет ДБР. Если получено не ДБР, то М-метод. Будет рассмотрен дальше. 1 шаг. Осн – х3, х4, х5, х6.
Х3 = 18 – х1 – 3х2 Х4 = 16 – 2х1 – х2 (1) Х5 = 5 – х2 Х6 = 21– 3х1 Неосновные = 0àХ1 =(0; 0; 18; 16; 5; 21) соответствует вершине О(0; 0). Решение – допустимое, м.б. оптимальным. Проверим. Выразим целевую функцию через неосновные переменные F=2x1 + 3х2. При решении Х1 значение функции F(X1) = 0. Функцию можно увеличить за счет увеличения любой из неосновных переменных, входящих в уравнение для функции с положительным коэффициентом. Это можно осуществить перейдя к такому новому ДБР, в котором эта переменная будет основной, т.е. принимать не нулевое, а положительное значение (если новое решение будет вырождено, то функция цели сохранит свое значение). Одна из переменных, при этом из основных – в неосновные. Геометрически – к соседней вершине. В данном примере и х1 и х2 м можно. Выберем х2 – больший коэффициент. Система (1) накладывает ограничения на рост переменной х2. Т.к. необходимо сохранять допустимость решений, т.е. все переменные неотрицательны, то должны выполняться неравенства (х1 при этом = 0 как неосновная):
Каждое уравнение системы (1), кроме последнего, определяет оценочное отношение – границу роста переменной х2, сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при х2 при условии, что эти числа имеют разные знаки. Граница - ¥: § Последнее уравнение системы не ограничивает рост переменной х2, т.к. эта переменная не входит в него (входит с 0 коэффициентом). § Когда свободный член и коэффициент при переменной имеют одинаковые знаки, так как и в этом случае нет ограничения на рост переменной. § Не накладывает ограничений на рост переменной, переводимой в основные, и такое уравнение, где свободный член = 0, а переводимая переменная имеет знак +. При свободном члене = 0, а переводимая переменная имеет знак – уравнение ограничивает рост переменной 0. В данном примере наибольшее возможное значение для х2 = min{18/3; 16/1; 5/1; ¥} = 5. При х2 = 5 переменная х5 обращается в 0 и переходит в неосновные. Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные (т.е. где оценка минимальна) называется разрешающим. В данном случае – 3. выделяется рамкой в системе ограничений.
2 шаг. Осн – х2, х3, х4, х6. Неосн – х1, х5.
Х3 = 18 – х1 – 3(5 – х5) Х4 = 16 – 2х1 – (5 – х5) (2) Х6 = 21– 3х1 или
Х3 = 3 – х1 + 3 х5 Х4 = 11 – 2х1 + х5 Х6 = 21– 3х1
Неосновные = 0àХ2 =(0; 5; 3; 11; 0; 21) соответствует вершине А(0; 5). Решение – допустимое, м.б. оптимальным. Проверим. Выразим целевую функцию через неосновные переменные F=2x1 + 3х2 = 2х1+ 3(5 – х5) = 15+ 2х1 – 3х5. При решении Х2 значение функции F(X2) = 15. Изменение значения линейной функции можно определить заранее как произведение наибольшего возможного значения переменной, переводимой в основные, на ее коэффициент в целевой функции (изменение F = 5 * 3 =15. Значение F2 не является макс, т.к., повторяя рассуждения шага 1, можно обнаружить возможность дальнейшего увеличения лин функции за счет переменной х1, входящий в выражение для F с положительным коэффициентом. Система (2) определяет наибольшее возможное значение для х1 = min{¥; 3/1; 11/2; 21/3} = 3. второе уравнение – разрешающее, переменная х3 обращается в 0 и переходит в неосновные, при этом приращение целевой функции = 3*2 = 6.
3 шаг. Осн – х1, х2, х4, х6. Неосн – х3, х5. Выражаем новые основные переменные через новые неосновные, начиная с разрешающего уравнения. После преобразования получаем:
Х2 = 5 – х5 Х4 = 5 + 2х3 - 5х5 (3) Х6 = 12 + 3х3 – 9х5
Неосновные = 0àХ3 =(3; 5; 0; 5; 0; 12) соответствует вершине В(3; 5). Решение – допустимое, м.б. оптимальным. Проверим. Выразим целевую функцию через неосновные переменные F=2x1 + 3х2 = 2(3 – х3 +3х5) + 3(5 – х5) = 21- 2х3 + 3х5. При решении Х3 значение функции F(X3) = 21. Значение F3 не является оптим, т.к. можно обнаружить возможность дальнейшего увеличения лин функции за счет переменной х5, входящий в выражение для F с положительным коэффициентом. При определении наибольшего возможного значения для х5, которую переводим в основные, обратить внимание, что первое уравнение системы (3) не дает ограничения на рост х5, т.к. свободный член и коэффициент при х5 имеют одинаковые знаки. Система (3) определяет наибольшее возможное значение для х5 = min{¥; 5; 1; 12/9} = 1. Третье уравнение – разрешающее, переменная х4 обращается в 0 и переходит в неосновные, при этом приращение целевой функции = 1*3 = 3.
4 шаг. Осн – х1, х2, х5, х6. Неосн – х3, х4.
Х1 = 6 + 1/5х3 – 3/5х4 Х2 = 4 – 2/5х3 + 1/5х4 Х5 = 1 + 2/5х3 – 1/5х4 (3) Х6 = 3 – 3/5х3 + 9/5х4
Неосновные = 0àХ4 =(6; 4; 0; 0; 1; 3) соответствует вершине С(6; 4). Решение – допустимое, м.б. оптимальным. Проверим. Выразим целевую функцию через неосновные переменные F=2x1 + 3х2 = 24 – 4/5х3 – 3/5х4. При решении Х4 значение функции F(X4) = 24. Значение F4 является оптим, т.к. нет положительных коэффициентов при неосновных переменных. Вспоминая экономический смысл всех переменных, можно сделать следующие выводы: § Прибыль предприятия примет макс значение 24 руб. при реализации 6 ед. продукции первого вида (х1 = 6) и 4 ед. продукции второго вида (х2 = 4). § Дополнительные переменные х3, х4, х5 и х6 показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е. остатки ресурсов. При оптим плане производства х3 = х4 = 0, т.е. остатки первого и второго ресурсов равны 0, а остатки третьего и четвертого ресурсов равны соответственно 1 и 3 единицам.
В общем виде можно сформулировать критерий оптимальности при отыскании макс лин функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально. При отыскании мин лин функции Z возможны два пути: 1) отыскать макс лин функции F, полагая, что F = - Z и учитывая, что Zmin = - Fmax; 2) модифицировать симплексный метод: на каждом шаге уменьшать лин функцию за счет той неосновной переменной, которая входит в выражение лин функ с отрицательным коэффициентом. В общем виде можно сформулировать критерий оптимальности при отыскании мин лин функции: если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально. Замечание. На каждом шаге симплексного метода какая-либо неосновная переменная переводится в основные, при этом каждое уравнение системы ограничении определяет конечное или бесконечное наибольшее возможное значение этой переменной – оценочное отношение. Могут встречаться различные случаи оценки роста неосновной переменной, которые зависят от знаков и значений свободного члена и коэффициентов при переводимой переменной. Введем обозначения: Xi – переводимая неосновная переменная; Bj– свободный член; Aij – коэффициент при Xi; Сформулируем все возможные случаи оценки роста Xi в уравнении Xj = Bj + … + AijXi + …: 1) Хi = ½Bj/Aij½, если Bj и Aij разного знака и Aij не = 0, Bj не = 0. 2) Хi = ¥, если Bj и Aij одного знака и Aij не = 0, Bj не = 0. 3) Хi = 0, если Bj = 0 и Aij > 0. 4) Хi = ¥, если Bj = 0 и Aij < 0. 5) Хi = ¥, если Aij = 0.
|

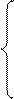 при ограничениях:
при ограничениях: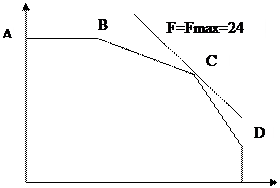
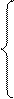 Перейдем к канонической форме с помощью дополнительных неотрицательных переменных:
Перейдем к канонической форме с помощью дополнительных неотрицательных переменных: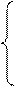 Неосн – х1, х2.
Неосн – х1, х2.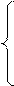 Х3 = 18 – 3х2 >= 0
Х4 = 16 – х2 >= 0
Х5 = 5 – х2 >= 0
Х6 = 21 >= 0
Х3 = 18 – 3х2 >= 0
Х4 = 16 – х2 >= 0
Х5 = 5 – х2 >= 0
Х6 = 21 >= 0
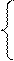 Х2 <= 18/3
Х2 <= 18/1
Х2 <= 5/1
Х2 <= 18/3
Х2 <= 18/1
Х2 <= 5/1
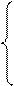 Х2 = 5 – х5
Х2 = 5 – х5


