Например, уравнение
определяет сферу радиуса R с центром в начале координат. При помощи поворотов и параллельного переноса осей координат всякое уравнение вида (25) может быть преобразовано к каноническому виду. Рассмотрим далее основные канонические уравнения, соответствующие типы поверхностей второго порядка и их наиболее важные свойства. 4.1.

    Уравнение (26) называется канони-ческим уравнением эллипсоида. Величины a, b, c - полуоси эллипсоида (рис. 10). Сечением эллипсоида любой плоскостью, параллельной координатным плоскостям, является эллипс (в частном случае окружность). Уравнение (26) называется канони-ческим уравнением эллипсоида. Величины a, b, c - полуоси эллипсоида (рис. 10). Сечением эллипсоида любой плоскостью, параллельной координатным плоскостям, является эллипс (в частном случае окружность).
Координаты точек эллипсоида удовлетворяют неравенствам - a £ x £ a, - b £ y £ b, - c £ z £ c. В частном случае, при a=b, эллипсоид является поверхностью вращения, получающейся при вращении вокруг оси Oz эллипса
4. 2. Гиперболоиды. Гиперболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
Рис. 11 Рис. 12
Гиперболоид, определяемый уравнением (27), называется однополостным (рис. 11); гиперболоид, определяемый уравнением (28), называется двуполостным (рис. 12). Для обоих видов гиперболоидов сечения, параллельные оси Oz - гиперболы (для однополостного гиперболоида в сечении может быть пара пересекающихся прямых); сечения, параллельные плоскости xOy - эллипсы. Величины a, b, с называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (27), только первые из них (a и b) показаны на рис. 11. В случае двуполостного гиперболоида, заданного уравнением (28), одна из них (именно с) показана на рис. 12. Замечание. При a=b гиперболоиды являются поверхностями вращения. 4.3. Параболоиды. Параболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими уравнениями
где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (29), называется эллиптическим (рис. 13). Сечения эллиптического параболоида, параллельные оси Oz - параболы; сечения, параллельные плоскости xOy - эллипсы. Параболоид, определяемый уравнением (30), называется гиперболическим (рис. 14). Сечения гиперболического параболоида, параллельные плоскостям yOz и xOz - параболы; сечения, параллельные плоскости xOy - гиперболы. Замечание. В случае, когда p = q, эллиптический параболоид (29) является поверхностью вращения (вокруг оси Oz).

Рис. 13 Рис. 14
 Конус, определяемый уравнением Конус, определяемый уравнением 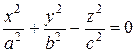 , имеет вершину в начале координат (рис. 15). , имеет вершину в начале координат (рис. 15).

          Поверхность конуса состоит из прямолинейных образующих, проходящих через его вершину и через точки эллипса с полуосями a и b, плоскость которого перпендикулярна оси Oz и находится на расстоянии с от начала координат. Поверхность конуса состоит из прямолинейных образующих, проходящих через его вершину и через точки эллипса с полуосями a и b, плоскость которого перпендикулярна оси Oz и находится на расстоянии с от начала координат.
 
4.5.Цилиндры. Поверхности цилиндров состоят из прямых линий (образующих), параллельных оси Oz. Сечениями (перпендикулярными оси Oz) эллипти-ческого цилиндра (его уравнение Пример 20. Определить вид поверхности
используя метод сечения плоскостями. Решение. Уравнение поверхности не содержит членов с произведением координат, следовательно плоскости симметрий параллельны координатным плоскостям. Пересекая поверхность плоскостями
Так как Пересекая поверхность плоскостями
гиперболы с действительной осью, параллельной оси Ox. При пересечении данной поверхности плоскостями
Последнее уравнение при Таким образом сечениями поверхности плоскостями являются эллипсы и гиперболы, действительные оси которых параллельны. Следовательно, исследуемая поверхность - двуполостный гиперболоид. Его уравнение можно преобразовать к каноническому виду:
|

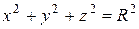


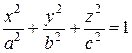 . (26)
. (26)

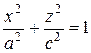 , лежащего в плоскости xOz. При a = b = с эллипсоид представляет собой сферу.
, лежащего в плоскости xOz. При a = b = с эллипсоид представляет собой сферу.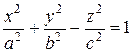 , (27)
, (27)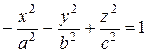 . (28)
. (28)



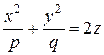 , (29)
, (29)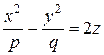 , (30)
, (30)

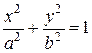 ), гиперболического цилиндра (его уравнение
), гиперболического цилиндра (его уравнение 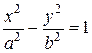 ) и параболического цилиндра (его уравнение
) и параболического цилиндра (его уравнение 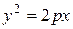 ) соответственно являются эллипсы, гиперболы и параболы.
) соответственно являются эллипсы, гиперболы и параболы.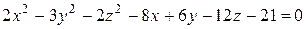 ,
,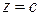 параллельными плоскости xOy, получим:
параллельными плоскости xOy, получим: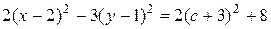 .
.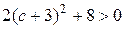 для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.
для любого с, полученная кривая является гиперболой с действительной осью, параллельной оси Ox.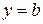 аналогично получаем уравнение
аналогично получаем уравнение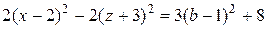
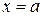 , параллельными координатной плоскости yOz, получаем:
, параллельными координатной плоскости yOz, получаем: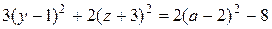 .
.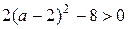 ,т.е. при
,т.е. при 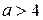 и
и 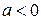 , есть уравнение эллипса.
, есть уравнение эллипса.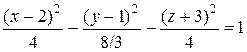 .
.


