Моделирование переходного процесса в замкнутом контуре регулирования
Существуют различные способы моделирования на ЭВМ переходных процессов в динамических системах. Выбор алгоритмов моделирования в основном определяется формой математического описания системы и имеющимся программным обеспечением. Если система задана обыкновенными дифференциальными уравнениями, то чаще всего применяют численные методы интегрирования. Наиболее распространенной в программном обеспечении ЭВМ является реализация метода Рунге – Кутта. Если динамическая система задана структурной схемой, то переходные процессы в ней удобно строить при помощи метода структурного моделирования. Суть метода состоит в том, что ЭВМ по рекуррентным формулам последовательно вычисляет значения выходов отдельных звеньев системы в дискретные равностоящие моменты времени. Для всех линейных звеньев первого порядка формула построения переходного процесса имеет следующий вид:
где a1, a2, a3 – числовые коэффициенты, зависящие от типа и параметров звена, а также от выбранной величины интервала ∆t. Где ∆t – это максимально допустимый период дискретности, при котором достигается высокая точность моделирования переходного процесса. Для высокой точности моделирования переходных процессов в звене ∆t должно быть достаточно малым. Значения коэффициентов a1, a2, a3 и максимально допустимые величины интервалов ∆t для звеньев первого порядка берем из таблицы. Таблица 1
Для объекта формула выглядит в виде колебательного звена, поэтому звено заменим эквивалентной схемой:
Рис.1.1
Рис.1.2 Расчетная схема примет вид:
Рис.1.3 Графики u(t) и y(t) представлены на рисунке 1.4
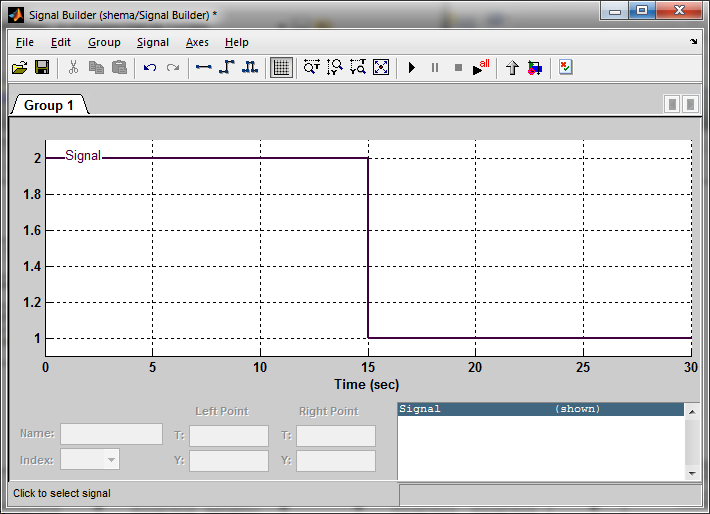
Описание блоков схемы: Signal Builder:
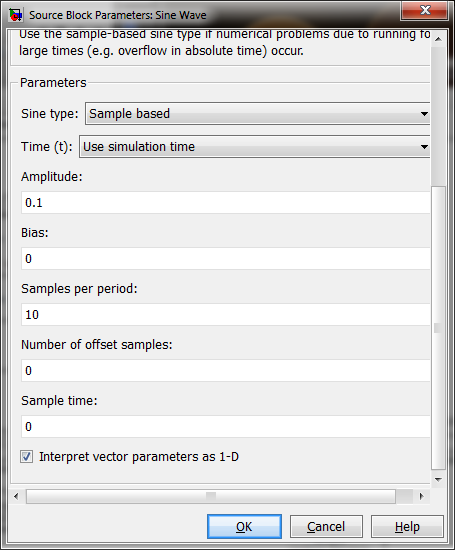
Sin wave1: Saturation1:
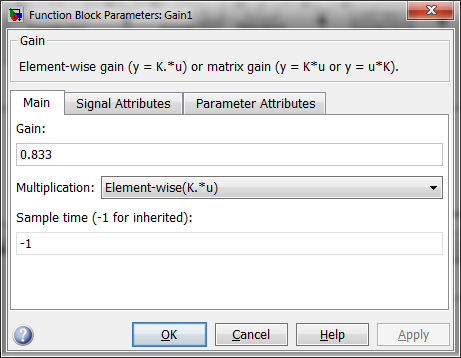
Uniform Random number1: Gain1:
Расчетные коэффициенты звеньев: 1) a11=1; a12=(0,5*dt)/2; a13=a12;
2) a21= exp(-dt/0.1); a22=2/dt*(0.1*a21-0.1+dt); a23=-2/dt*(0.1*a21-0.1+a21*dt);
3) a31= exp(-dt/1.5); a32=1/dt*(1.5*a31-1.5+dt); a33=-1/dt*(1.5*a31-1.5+a31*dt);
4) a41=1; a42=(0,15*dt)/2; a43=a42;
Выбираем наименьший период дискретности, равный 0.005, В цикле используем Алгоритм моделирования
Рис 1.4 1. Объявляем массивы, в которых будут храниться значения входов и выходов структурных звеньев. 2. Вводим значения всех сигналов в момент времени t=0. Поэтому x(1)=2; v1(1)=0; v2(1)=0; v3(1)=0; v4=zeros(1,6000); vm=zeros(1,6000); y=zeros(1,6000); e(1)=x(1)-y(1); z1(1)=K1*e(1); r1(1)=v1(1)+z1(1); f1(1)=0; f2(1)=0; u(1)=f1(1)+v2(1); J(1)=u(1)-v4(1)*K2; 3. В цикле считаем, значения всех сигналов в системе через время ∆t. Цикл организуется с помощью оператора for(). На вход системы подается сигнал: DT=6000; for n=2:1:DT %вх сигнал if n<=3000 x(n)=2; else x(n)=1; end … end 4. Регулятор описывается следующим образом: %регулятор v1(n)=a11*v1(n-1)+a12*e(n)+a13*e(n-1); r1(n)=v1(n)+K1*e(n); 5. Исполнительный механизм описывается так: %исполнительный механизм v2(n)=a21*v2(n-1)+a22*r1(n)+a23*r1(n-1); 6. Ограничитель: if (v2(n)>=0) && (v2(n)<=4) vm(n)=v2(n); elseif v2(n)<0 vm(n)=0; elseif v2(n)>4 vm(n)=4; end 7. Внешнее воздействие на систему задается с помощью условия: f1=0.1*sin(0.11*n*dt); 8. Объект имеет вид: %объект управления J(n)=u(n)-v4(n-1)*K2; v3(n)=a31*v3(n-1)+a32*J(n)+a33*J(n-1); v4(n)=a41*v4(n-1)+a42*v3(n)+a43*v3(n-1); 9. Шум с равномерным законом распределения в диапазоне [-0.01;0.01]: %Создаем матрицу в 6000 элементов %в пределах от 0 до 1 R=rand(1,6000); a=-0.01; b=0.01; %Равномерно распределенная %случайная величина от -0.01 до 0.01 f2=R*(b-a)+a; 10. По результатам моделирования получаем массивы значений vm(t) и y(t). Текст программы на языке MatLab приведен в приложении. В результате работы программы (см. приложение №1) получили значения массивов vm и y, графики которых приведены на рисунке (рис.1.5):
Рис.1.5
|

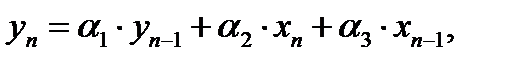 (1.1)
(1.1)
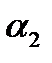
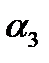
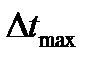

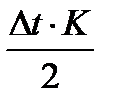


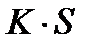

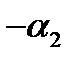

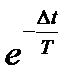

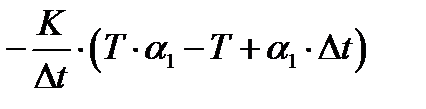
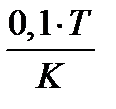







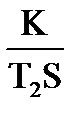








 ;
;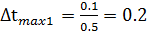 ;
; ;
; ;
; ;
; ;
;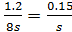 ;
;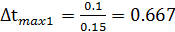 ;
;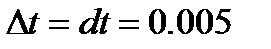
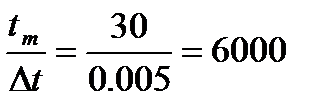 значений.
значений.




