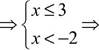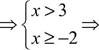Приклади. Приклад 1. Розв язати нерівність / (х) = -—( 3)— > 0.

,/ ч (х- 1)(х + 2)² _Л

Приклад 1. Розв язати нерівність / (х) = -—(3)— > 0.

А Позначимо на числовій вісі розв'язки чисельника й знаменника х =-3, х₂ =-2, х₃ =1. Вираз / (х) має різні знаки на інтервалах

-3),(-3,-2),(-2,1),(1, Візьмемо будь-яку точку з інтервалу -3), наприклад х = -4, і розглянемо, чому дорівнює / (-4):

(-4 -1) • (-4 + 2)² -5 • 4

/ (-4) = ^------ / ¹ _ч—'— = —— = 20 > 0.

^v ' (-4 + 3) -1

Звідси випливає, що /(х) > 0 при усіх хє -3).

При проходженні через точку х=-3 змінить знак тільки вираз у дужках, що розташован у знаменнику, а знак виразів в інших дужках залишаться без зміни. Отже, /(х) змінить знак і /(х) < 0 для усіх хє (-3,-2).

При проходженні через точку х=-2 / (х) не змінить знака, тому що ви­раз у дужках (х+2) у парній степені, і, отже, значення виразу (х+2)² не може бу­ти від'ємним.

Відповідь: (-гс, -3)и{-2]и[1,.►

Приклад 2. Розв'язати нерівність

3х + 2 2 х + 5

А Найпоширеніша помилка - множення на знаменник. Треба пам'ятати, що при множенні нерівності на від'ємне число знак нерівності змінюється.

■3.

<

Рис. 1.12. Розв'язок нерівності мето­дом інтервалів

При проходженні через точку х=+1 / (х) знову змінить знак. Треба бути уважним! Зазвичай значення х = -2 втрачають.

Перенесемо вираз, що знаходиться в правій частині нерівності, у ліву частину і зведемо до спільного знаменника.

<0 17/

х +

18 х2 + 52 х + 34 (3х + 2)(2 х + 5)

< 0

< 0

2 (2 х + 5)- 3 (3 х + 2) + 3 (3 х + 2)(2 х + 5)

(3х + 2)(2 х + 5)

18 (х +1

^ ^ і

(3х + 2)(2 х + 5)

 

а • х2 + Ь • х + с = а(х - х1)(х - х2) = 18(х +1)(х +179 -52 ±у/522 - 4 • 18 • 34 -13 ±7132 - 9 • 17 -13 ± 4

1,2

Рис. 1.13. Розв'язок нерівності методом інтервалів

х

Розставляючи знаки як у попе­редньому прикладі, одержуємо відповідь:

с

5 17

и

х <

Л

, г',-3

У

 

Приклад 3. Розв'язати рівняння: |3 - х| - |х + 2| = 5.

А1 спосіб розв'язування

Розглянемо 4 можливих випадки:

 

У першому випадку одержуємо рівняння 3 - х - (х + 2) = 5 ^ х = -2.

3 - х > 0 х + 2 > 0 Рис. 1.14. Область дозволених зна­чень у першому випадку

х < 3 х >-2

1)

^ -2 < х < 3 (ОДЗ).

Це значення задовольняє ОДЗ, то­му є розв'язком даного рівняння.

У другому випадку одержуємо рівняння 3-х + х + 2 = 5^5 = 5. Тут х є (-го, +го), але з урахуванням ОДЗ

Рис. 1.15. Область дозволених зна­чень у другому випадку

3 - х > 0 х + 2 < 0

х < -2 (ОДЗ).

2)

х <-2 Розв'язок: х є (-го,-2)

 

3)

_________ -2__________ ^ У третьому випадку одержуємо

3 - х < 0 х + 2 > 0

х > 3 (ОДЗ).

рівняння х-3-(х + 2) = 5=>-5 = 5. Рис. 1.16. Область дозволених зна- Р_озв'_язкі_{в немає} чень у третьому випадку

3 - х < 0 х + 2 < 0

х > 3 х <-2

4)

(ОДЗ).

Аналогічно знаходимо знаки виразів у модульних дужках для інтервалу х є (-2, +3). Позначимо на числовій вісі ці знаки «+» і «+». Тобто,

3 - х - х - 2 = 5 ^ х = -2. Значення х = -2 не входить в ОДЗ, тому розв'язків немає.

Аналогічно знаходимо знаки виразів у модульних дужках для інтервалу хє [+3,. Позначимо на числовій вісі ці знаки «-» і «+». Тобто:

-3 + х - х - 2 = 5 ^ - 5 = 5. Розв'язків немає.

Відповідь: хє -2].►

Приклад 4. Розв'язати рівняння: у]х + 2 - х +1 = 0. А Знайдемо ОДЗ: х >-2.

Залишаємо вираз, що містить квадратний корінь, у лівій частині рівнян­ня, а всі інші доданки переносимо в праву: у/х + 2 = х -1. Підносимо до квадрату: х + 2 = (х -1)^[1],

Оскільки -\]х + 2 > 0, то для коректності піднесення до квадрату необхід­но, щоб х -1 > 0 ^ х > 1. Таким чином змінюємо ОДЗ: х > 1. Одержимо рівняння х² - 3х -1 = 0.

_й, 3 ±7 9 + 4 • 1 3 ±л/1з

Знайдемо його розв язки: х₁₂ = —

2 2

х = 2(3-л/Й), х₂ = 2(3 + >/1з).

Обидва розв'язки задовольняють ОДЗ, але тільки один х = -(3 + Т13) задовольняє додатковому обмеженню х > 1. Відповідь: х = 1 (3 + л/Ї3).►

Приклад 5. Розв'язати рівняння: \Іх² - 6х + 9 - Vх + 2 = -1. А Знайдемо ОДЗ: х >-2.

Переносимо другий вираз, що містить радикал, у праву частину рівнян­ня, а (-1) переносимо в ліву частину:

V х² - 6 х + 9 +1 = л/ х + 2. Підкореневий вираз представимо у вигляді добутку, для чого знайдемо його розв'язки:

= 6 ±У 36 - 4 • 9 = _

^х, 2 — — ^[2].

^1,2 2

Тобто, рівняння матиме вигляд:^(х-3)² +1 = л/х + 2. У цьому місці часто допускається типова помилка:

х - 3) = х - 3. 32

Насправді правильним буде вираз: ^(х- 3)² = |х - 3|.

Необхідно завжди пам'ятати про модульні дужки при розкритті подібних виразів, у противному випадку будуть втрачені розв'язки рівняння. Таким чином, одержуємо вираз:

|х - 3 +1 = Vх + 2.

Розглянемо два випадки:

1) х - 3 > 0 ^ х > 3 (ОДЗ). Розкриваємо модульні дужки зі знаком "+": х - 3 +1 = л/ х + 2 ^ х - 2 = >/ х + 2.

Підносимо до квадрату обидві частини рівняння: (х - 2) = х + 2,

Для коректності піднесення до квадрату виразу л/х + 2 > 0 необхідно, щоб х-2>0 ^ х>2. Це додаткове обмеження не змінює ОДЗ.

Розкриємо вираз у дужках і перенесемо всі доданки з правої частини рів­няння в ліву. Одержимо рівняння х² - 5х + 2 = 0.

5 + л/Ї7 5-л/Ї7 „, 5 + л/Ї7 х₁ =---------------------------------------, х₂ = —. Тільки один розв язок х₁ =—-- задоволь­няє ОДЗ х > 3.

2) х - 3 < 0 ^ х < 3 (ОДЗ).

Розкриваємо вираз у модульних дужках зі знаком "-": 3 - х +1 = >/ х + 2 ^ 4 - х = л/ х + 2 Підносимо до квадрату обидві частини рівняння:

(4 - х)² = х + 2.

Для коректності піднесення до квадрату виразу ^/х + 2 > 0 необхідно, щоб 4-х>0 ^ х<4. Це додаткове обмеження не змінює ОДЗ.

Розкриємо вираз у дужках і перенесемо всі доданки з правої частини рі­вняння в ліву. Одержимо рівняння х² - 9х +14 = 0.

9 + У25 9-У25 _Т., 9-^25 х₁ =-------------------------------------------------- = 7, х₂ = ----------- = 2. Іільки один розв язок х₂ =------------------------------------------- = 2

задовольняє ОДЗ х < 3.

Поєднуємо отримані розв'язки.

у[х 4У 3 ху = 9

Відповідь: х₁ = ⁵ +, х₂ = 2. ►

1 1

Приклад 6. Розв'язати систему рівнянь: А Знайдемо ОДЗ: х > 0, у > 0.

_З • 9 _бГ 9 3..

З другого рівняння знаходимо х = — або \Іх = — = —т= і підставляємо в

У \У ^У

 

УУ 1

{у - 2УУ - 3 = 0].

перше:

УУ 3

УУ •УУ - 3 - 2 •УУ 3 •УУ

 

Робимо заміну: і = УУ (і > 0). Одержуємо квадратне рівняння відносно

 

і: і² -2і-3 = 0.

 

Одержимо розв'язки: х₁₂ = 1 + 3 = 1 ± 2.

ї₁ =-1, ї₂ = 3. Але, відповідно до заміни, ї = -1 не підходить. Тому у[у = 3. Звідси у = 9, х = 1. Відповідь: (1; 9). ►

1.6. Індивідуальне завдання № 1.3

Студент повинен розв'язати одну з наведених нижче задач, вибравши її

 

за своїм номером у журналі групи.

Спростити вираз:

2.

1. 3. 5.

Ь + у[аЬ

1/2

6.

а

8.

9.

10.

а + 2^[аЬ + Ь ау[а - Ь4Ь

а - Ь а + х³ + 5 х² -14х

х² + 6 х - 7 У(аЬс + 4): а + 4>/Ь • с: а _- уІаЬс + 2 ³9х⁵ - 4 х

7. 2³ х² +

- Уэх² ' Ух +1 ^ 1

1/2.! а +1

12.

11.

+1

13.

хУх+х+ух х² - ух

5/4 1/4 а - а

3/4. 1/^ 1/^ 1/4 а + а а + а

8 х "³ + 8 х"² + 2 х

х - У х>/х - уТУ

х - У

5/4 1/4 а - а

+1;

1/2 +! а +1

3/4, 1/^ 1/2, 1/4 а + а а + а

2 2 х + Ух - 6 У

~ ₀ 2 '

п - т

(т + п);

-0,5 ' ^ Уа

х - Ух - 2 У

т - п

2 2 2 V т + тп т - п

х -1 х +1

+

У 3

а

а+2

У

х + х⁷² +1 х ² -1

а + 2

У2а У2а + 2 а-У2а

 

15.(х-2)2 (х +1) = (1,5х-3)(х2 - 4);

0,25 х² + х +1

Знайти суму розв'язків рівняння: 14. |х +1 = 2|х - 2; 16. х² - 2х = |х -1.

Знайти добуток розв'язків рівняння:

17. 2 (х² + 5)—= 17.

¹ ' х² + 5

Обчислити різницю між найбільшим і найменшим коренями рівняння:

8 7 8 7

18. ------- + -2------ = -2; 19. -------- + -2------ = -2;

х - 8 х - 7 х - 8 х - 7

20. х² + ІхІ = ⁵.

Знайти середнє арифметичне всіх дійсних розв'язків рівняння:

1 1 =₅1 _{3 3} ²¹. ф + 1)^-(_х + ₀,₅)2 - ⁵3^{; 22}. (х-³)(х-¹)³ +(³-х)(х-²)³ = ⁷(х-³)

Звільниться від ірраціональності у знаменнику: 14 4

²³. ^{; 24}. 413 - 49

Знайти:

25. Суму кубів дійсних розв'язків рівняння 1 1 1

х³ + 4 х³ + 5 56 '

3х 232 2

26. Значення виразу,— г= + у;

л/3х + 34 у

27. Значення виразу ^3х°

х2 + 8

якщо х₀ - розв'язок рівняння л/х - 4 • V2х - 7 = х - 2;

28. Суму виразів \І24-ї² і48-ї², якщо відомо, що їхня різниця дорівнює 2 (значення змінної ї знаходити не потрібно);

... _,. 2х 3х +1 3

29. Розв язати рівняння---------------------------- = 0;

х -1 х² -1 х +1

х² -4)(х³ -1

30. Розв'язати нерівність -—2— -------------- > 0;

х2 + 6 х + 5 > 0 х2 - 25 < 0 2 х +11 > 0.

х - 2 х - 3

31. Розв'язати систему нерівностей

1.7. Логарифмічні рівняння й нерівності

Логарифмування - це дія, що полягає у знаходженні логарифма число­вого, алгебраїчного або іншого виразу. Логарифмування - одна з двох дій, зво­ротних до піднесення до ступеня: якщо а = с, то а = РС і Ь = \ogaC. В обчис­лювальній практиці логарифмування вживається для зведення дій множення, ділення, піднесення до ступеня і добування кореня до дій додавання, відніман­ня, множення і ділення.

Розв'язок логарифмічних рівностей ґрунтується на наступних форму­лах:

 

(log^=b) ^{ct = x), де a > 0, а Ф 0;

=1; logc1=0;

^log c^b =,

Cl0gCX = X;

log _ba ^logаХУ = ^loga^x + ^logаУ;

log _ax = k ■ log _ax, де X >0;

^log_am^b = — ■ ^loga^b = ^loga ^;

logaX = logaX - logсУ; logbx = У log ab

^u m ^loga^b = ^log_am^b;

 

Для розв'язування логарифмічних нерівностей виду 1о§_а/(х)>(<)1о§_а^(х) необхідно використовувати співвідношення:

ОДЗ: /х) >0; ^х)>0; /х) ф 1; Іо^д^х) = а. Якщо а>1, то: /х)>^(х); якщо 0<а<1, то: /х)<^(х).