Модель нейрона с сигмоидой на выходеСтруктура нейрона с сигмоидой на выходе аналогична структурам ранее обсуждавшихся моделей, т.е. персептрона и нейрона типа Адалайн (см. рисунок 2.10).
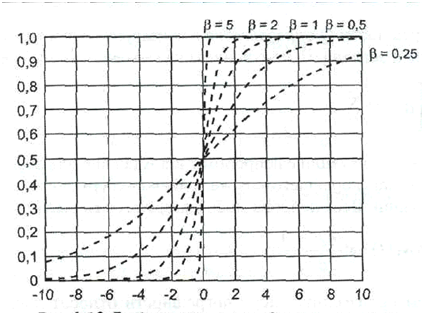
Рис. 2.10. График униполярной функции активации при различных значениях параметра β
Название обусловлено функцией активации, которая имеет форму сигмоидальной униполярной или биполярной функции. Это непрерывные функции, описывающиеся выражениями: - униполярная функция
- биполярная функция
На рисунке 2.10 представлены графики униполярных функций при различных значениях параметра бетта. Читатель может заметить, что при малых значениях параметра бетта функция имеет плавный характер, но с ростом значения этого параметра график становится более крутым вплоть до обретения порогового вида. Огромным достоинством сигмоидальных нейронов считается дифференцируемость функции активации. Кроме того, производные этих функций легко вычисляются, поскольку они приобретают следующие формы: - для униполярной функции:
- для биполярной функции:
Структура нейрона с сигмоидой на выходе представлена на рис. 6.11. Выходной сигнал описывается выражением
Рис. 2.11. Структура нейрона с сигмоидой на выходе
Мера погрешности Q определяется как квадрат разности между эталонным значением и значением, полученным на выходе нейрона, т.е.:
Так же, как и в ситуации с нейроном типа Адалайн, для обучения используется правило наискорейшего спуска, однако теперь должна учитываться функция активации. Веса нейрона модифицируются согласно выражению
Рассчитаем производную меру погрешности относительно весов. Очевидно, что
Следовательно
Легко заметить, что
Введем обозначение
Согласно формулам (2.60) и (2.65), веса на шаге (t +1) модифицируются следующим образом: wi(t +1)= wi(t)-ηδxi = wi(t) + η(d - f(s)) f'(s)xi. (2.66)
Теперь рассмотрим альтернативный способ обучения сигмоидального нейрона с применением алгоритма RLS. Рассмотрим два случая, различающиеся способом определения погрешности. В первом случае сигнал погрешности определяется на выходе линейной части нейрона. Поэтому мера погрешности имеет вид
где
 (2.68) (2.68)
В этой ситуации погрешность интерпретируется как заданный сигнал на выходе линейной части нейрона. Нормальное уравнение принимает вид
либо в векторной форме
r(t) = R(t) w(t), (2.70) где
Обратим внимание, что уравнения (2.71) и (2.72) аналогичны уравнениям (2.34) и (2.35). Поэтому алгоритм RLS принимает форму
e(t)=b(t)- x T(t) w (t-1)=b(t)-s(t); (2.73)
P(t)=λ-1[I-g(t)xT(t)]P(t -1); (2.75)
w (t) = w (t -1) + g (t)e(t), (2.76)
причем начальные условия определяются выражением (2.55). Во втором случае погрешность определяется на выходе нелинейной части нейрона. Мера погрешности имеет вид
В результате дифференцирования меры (2.77) относительно вектора w(t) и приравнивания полученного выражения к нулю получаем
Дальнейшие вычисления дают:
В результате применения подстановки Тейлора к содержимому квадратных скобок формулы (2.79) получаем
f(b(k)) ≈ f(S(k))+f'(s(k)))b(k)-s(k)), (2.80) где
b(t) = f-1(d(t)). (2.81)
В итоге выражения (6.79) и (6.80) сводятся к уравнению
Уравнение (2.82) в векторной форме имеет вид
r (t) = R (t) w (t), (2.83) где
При использовании в выражениях (2.73), (2.76) подстановок
х (k)→ f'(s(k)) x (k); (2.86)
b(k) → f'(s(k))b(k) (2.87)
получаем форму алгоритма RLS, адаптированную к обучению сигмоидального нейрона:
Начальные условия определяются в соответствии с формулой (2.55).
|



 (2.56)
(2.56)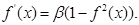 (2.57)
(2.57) (2.58)
(2.58)
 (2.59)
(2.59) (2.60)
(2.60)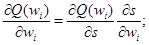 (2.61)
(2.61)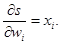 (2.62)
(2.62)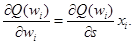 (2.63)
(2.63)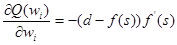 . (2.64)
. (2.64) . (2.65)
. (2.65)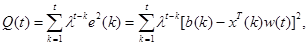 (2.67)
(2.67) , (2.69)
, (2.69)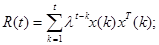 (2.71)
(2.71) (2.72)
(2.72) (2.74)
(2.74) (2.76)
(2.76)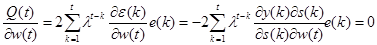 (2.78)
(2.78)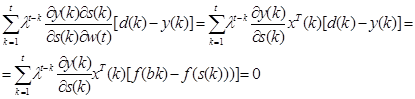 (2.79)
(2.79) . (2.82)
. (2.82) (2.84)
(2.84) (2.85)
(2.85)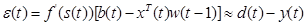 ; (2.88)
; (2.88) (2.89)
(2.89) (2.90)
(2.90)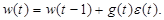 (2.91)
(2.91)


