Основы метода сетокРешение краевых задач в каждом конкретном случае является достаточно сложным процессом. Аналитическое решение даже одномерного уравнения теплопроводности, являющегося дифференциальным уравнением в частных производных параболического типа, трудноосуществимо, если иметь в виду зависимость теплофизических свойств от температуры, нелинейность граничных условий, т.е. зависимость их от температурного поля. Можно сказать, что аналитические методы оказываются практически непригодными для нахождения двух- и трехмерных температурных полей в областях сложной конфигурации. От этих недостатков свободны численные методы, в которых дифференциальные операторы заменяются алгебраическими, получающиеся матричные уравнения решаются на компьютерах с нахождением температурного поля в узловых точках конечно-разностной сетки. Основная идея численных методов состоит в замене непрерывных производных по времени и координатам, входящих в дифференциальные уравнения, описывающие неравновесные процессы переноса, а также в краевые условия их приближенными значениями в отдельных точках (узлах) конечно-разностной сетки. В результате такой замены дифференциальная краевая задача сводится к системе алгебраических (матричных) уравнений относительно искомых параметров в узлах и ячейках сетки. В общем случае расположение узлов сетки в исследуемой области может быть произвольным. Оно определяется особенностями решаемой задачи. На практике часто применяют сетку, равномерно покрывающую расчетную область. Такая сетка с постоянными расстояниями между ближайшими узлами (шагами сетки) называется регулярной. Фрагмент такой сетки применительно к одномерной нестационарной задаче показан на рис. 6.1. Узлы этой сетки определяются координатами
где N – число разбиений по толщине слоя Hx; hx, ht – соответственно шаги пространственной (по x) и временной (по t) сеток; i, k – номера узловых точек в направлении координат x, t.
Получим приближенные (аппроксимированные) формулы для первой и второй производных переносимой величины Т (t,x), входящей в дифференциальные уравнение теплопроводности. Для этого рассмотрим ее разложение в ряд Тейлора в направлении координаты x в окрестности точки x 0:
Ряд быстро убывает, и для нахождения приближенного значения первой производной можно ограничиться двумя членами разложения. Третий член разложения (6.29), являясь максимальным из отброшенных, характеризует в этом случае ошибку аппроксимации или ограничения. С точностью до ошибки аппроксимации можно записать первую производную в конечных разностях:
Выбирая узловые точки справа и слева от рассматриваемой точки x 0 на расстоянии шага hx (x=x 0 + hx, x=x 0 – hx), можно получить из (6.30) формулы право- и левосторонней разностей:
Для нахождения ошибки аппроксимации полученных выражений воспользуемся рядом Тейлора (6.29), учитывая в нем три члена разложения. Подставим в этот ряд значения x=x 0 и x=x 0 +hx и вычтем из второго уравнения первое, в результате получим
где Используя нумерацию узловых точек, можно записать полученные формулы односторонних разностей для i -й узловой точки на k -м слое по времени:
Среднее арифметическое значение право- и левосторонних разностей дает формулу центральной разности
Вторая производная может быть найдена формально как производная от производной с применением формул (6.33):
Отметим, что формулы центральной разности (6.34) и второй производной (6.35) имеют второй порядок точности, т. е. они на порядок точней формул односторонних разностей (6.33).
|

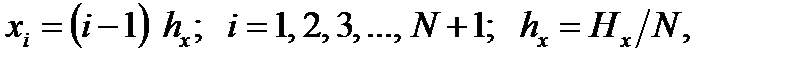
 , (6.28)
, (6.28) (6.29)
(6.29)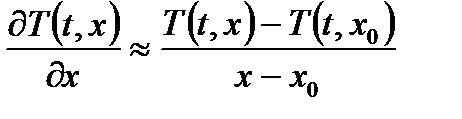 . (6.30)
. (6.30) ,
, 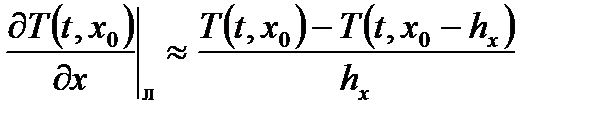 . (6.31)
. (6.31)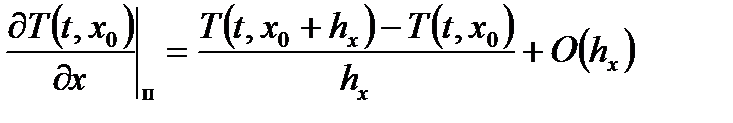 , (6.32)
, (6.32) – остаточный член ряда Тейлора, имеющий порядок шага сетки hx. В этом случае, имея в виду первую степень шага сетки в остаточном члене разложения, говорят, что формула (6.32) аппроксимации первой производной имеет первый порядок точности.
– остаточный член ряда Тейлора, имеющий порядок шага сетки hx. В этом случае, имея в виду первую степень шага сетки в остаточном члене разложения, говорят, что формула (6.32) аппроксимации первой производной имеет первый порядок точности. . (6.33)
. (6.33) . (6.34)
. (6.34)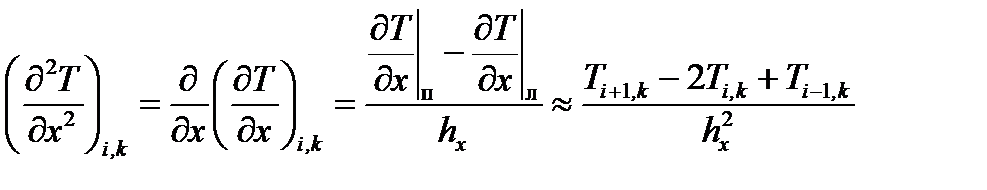 . (6.35)
. (6.35)


