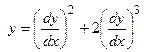Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Дифференциальное и интегральное исчисление функции одной переменной
Индивидуальные задания
| Пособие разработано ст. преп. Смышляевой Т. В.
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
|
Пермь 2007
Вариант решения заданий
I. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции 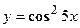
Решение:
- Придаем аргументу
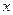 произвольное приращение
произвольное приращение 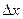 и, подставляя в данное выражение функции вместо
и, подставляя в данное выражение функции вместо 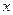 наращенное значение
наращенное значение 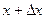 , находим наращенное значение функции
, находим наращенное значение функции 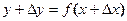
В данном случае 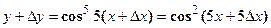
- Находим приращение функции
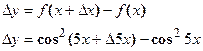
- Делим приращение функции на приращение аргумента, т. е. составим отношение
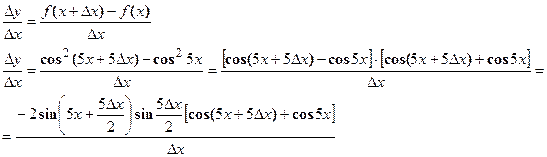
- Ищем предел этого отношения при
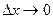 . Этот предел и даст искомую производную
. Этот предел и даст искомую производную 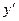 от функции
от функции 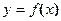 ;
; 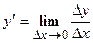
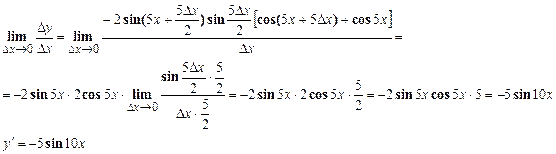
II. Производная сложной функции
Производная сложной функции равна произведению её производной по промежуточному аргументу на производную этого аргумента по независимой переменной.
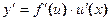
Найти производные следующих функций:
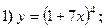
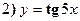
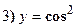
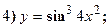
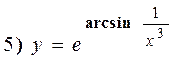
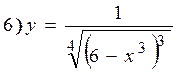
Решение:
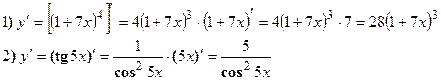
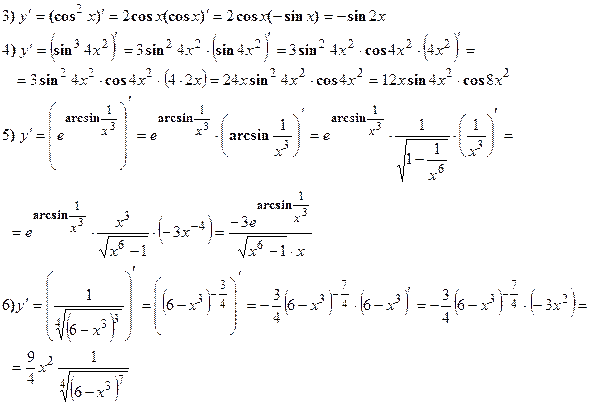
III. а) Производная неявной функции
Найти 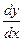 для данной неявной функции
для данной неявной функции 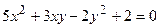
Решение:
Дифференцируем по 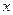 обе части равенства, где
обе части равенства, где 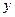 есть функция от
есть функция от 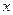 , получим
, получим 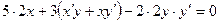 .
.
Учитывая, что 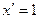 , получаем
, получаем
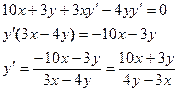
б) Логарифмическое дифференцирование
Логарифмическое дифференцирование полезно применять для нахождения производной от показательно - степенной функции 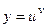 , где
, где 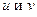 - функции от
- функции от 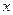 и когда заданная функция содержит логарифмирующиеся операции (умножения, деления, возведения в степень, извлечение корня).
и когда заданная функция содержит логарифмирующиеся операции (умножения, деления, возведения в степень, извлечение корня).
Найти производные следующих функций:
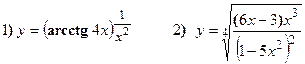
Решение:
Применяется логарифмическое дифференцирование, последовательно находим:
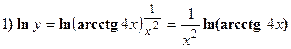
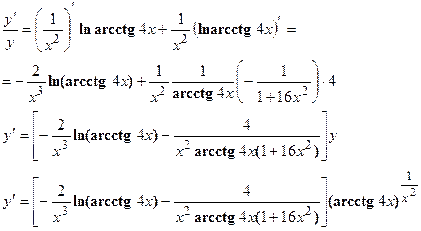
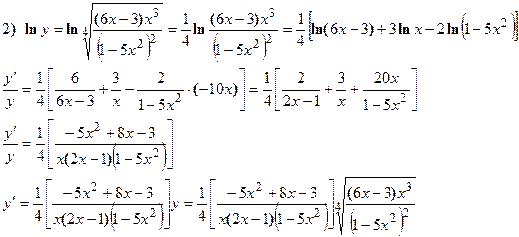
в) Производная от функции, заданной параметрически
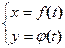
Производная 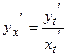
Найти производную  для функции, заданной параметрически
для функции, заданной параметрически 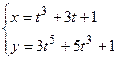
Решение:
Найдем 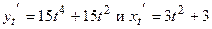 . Следовательно,
. Следовательно, 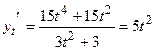
IV. Показать, что функция 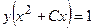 обращает уравнение
обращает уравнение 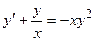 в тождество.
в тождество.
Решение:
Выразим 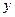 в явном виде
в явном виде  . Найдем
. Найдем 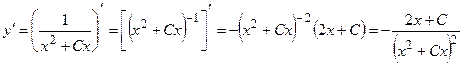
Подставляем 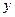 и
и 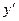 в левую часть уравнения, получаем
в левую часть уравнения, получаем 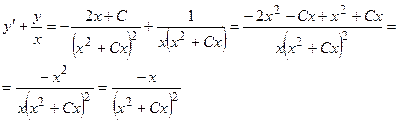
Подставляем 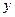 в правую часть равенства, получаем
в правую часть равенства, получаем 
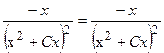 , что и требовалось доказать.
, что и требовалось доказать.
V. Производные высших порядков
а) Производная явной функции

Решение:
Дифференцируя функцию 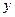 , получим
, получим 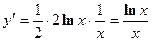 .
.
Дифференцируя производную 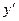 , получим
, получим 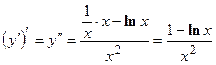
б) Производная неявной функции
Для данной неявной функции найти 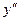 .
.
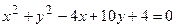
Решение:
Дифференцируем по 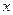 обе части равенства, где
обе части равенства, где 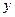 есть функция от
есть функция от 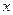 , получаем
, получаем 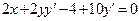
Отсюда найдем 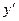 .
.
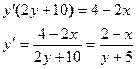
Найдем 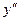 :
:
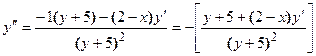
Подставляем в левую часть найденную производную 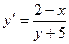 , получаем:
, получаем:
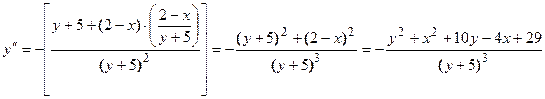 .
.
Учитывая, что 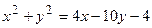 , получим
, получим 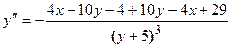 или
или 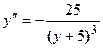
VI. Производная от функции, заданной параметрически
Для функции, заданной параметрически, найти  .
.
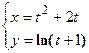
Решение:
Находим производные  по параметру
по параметру  .
.
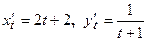
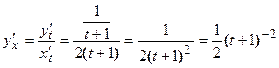
Далее находим производную от 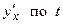 , а затем искомую вторую производную от
, а затем искомую вторую производную от 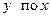 как отношение производных от
как отношение производных от 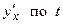 и от
и от 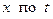 .
.
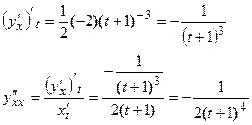
- Касательная и нормаль к кривой
Если плоская кривая отнесена к прямоугольной системе координат, то уравнение касательной и нормали к ней в точке 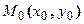 имеют вид:
имеют вид:
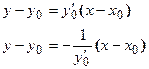 , где
, где 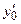 - значение в точке
- значение в точке 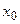 производной
производной 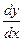 из уравнения кривой.
из уравнения кривой.
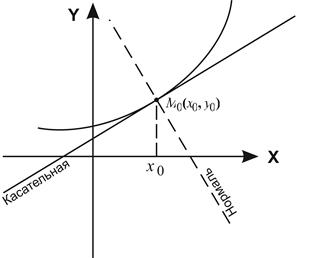
Найти уравнение касательной и нормали к эллипсу 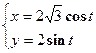 в точке, где
в точке, где 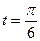 .
.
Решение:
При 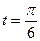 ,
, 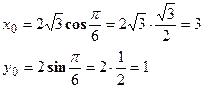 , получаем точку
, получаем точку 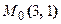
Найдем 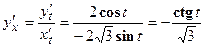
При 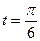 , получаем
, получаем 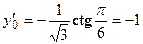 .
.
Уравнение касательной:
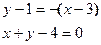
Уравнение нормали:
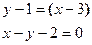
- Теорема Ролля, Лагранжа и Коши.
Теорема Ролля
Если функция 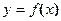 :
:
- непрерывна на отрезке [ a, b ]
- имеет конечную производную в каждой точке интервала (a, b)
- принимает равные значения на концах отрезка,
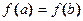 , то в интервале (a, b) существует по крайней мере одна точка с, в которой производная функции обращается в нуль:
, то в интервале (a, b) существует по крайней мере одна точка с, в которой производная функции обращается в нуль: 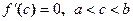 .
.
Функция  на концах отрезка [0, 4] принимает равные значения
на концах отрезка [0, 4] принимает равные значения 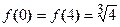 .
.
Справедлива ли для этой функции теорема Ролля на отрезке [0, 4]?
Решение:
Найдем 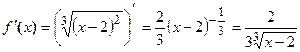 . При
. При 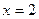 ,
, 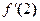 не существует. Нарушено второе условие теоремы Ролля.
не существует. Нарушено второе условие теоремы Ролля.
Теорема Лагранжа.
Если функция 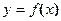 :
:
- непрерывна на отрезке [ a, b ]
- имеет конечную производную в каждой точке интервала (a, b), то найдется по крайней мере одна внутренняя точка с интервала (a, b),
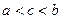 , для которой
, для которой 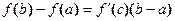 .
.
Проверить выполнение условий теоремы Лагранжа для функции  и найти соответствующее промежуточное значение с.
и найти соответствующее промежуточное значение с.
Решение:
Функция 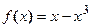 непрерывна и дифференцируема для всех значений
непрерывна и дифференцируема для всех значений 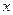 , причем
, причем 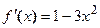 . Отсюда по формулам Лагранжа имеем
. Отсюда по формулам Лагранжа имеем

Следовательно, 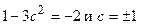 ; годится только значение
; годится только значение 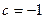 , для которого справедливо неравенство
, для которого справедливо неравенство 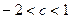 .
.
Теорема Коши.
Пусть функции 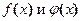 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
- непрерывна на отрезке [ a, b ]
- имеют конечные производные во всех точках интервала (a, b)
-
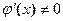 для любого
для любого 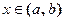 , то внутри отрезка [ a, b ] найдется такая точка
, то внутри отрезка [ a, b ] найдется такая точка 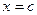 ,
, 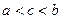 , что
, что 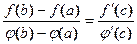
Проверить справедливость формулы Коши для функций 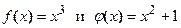 на отрезке [1; 2].
на отрезке [1; 2].
Решение:
Функции 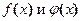 непрерывны и дифференцируемы при всех значениях
непрерывны и дифференцируемы при всех значениях 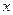 . Производные данных функций равны соответственно
. Производные данных функций равны соответственно 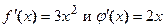 . На отрезке [1, 2],
. На отрезке [1, 2], 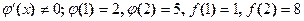 .
.
Тогда между двумя значениями 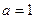 и
и 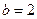 существует значение
существует значение 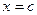 , удовлетворяющее равенству
, удовлетворяющее равенству 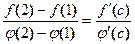
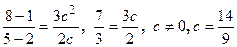 .
.
Вариант 1
1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции 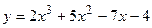
2. Найти производную сложной функции
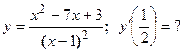
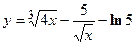
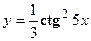
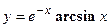
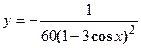
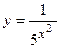
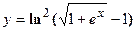
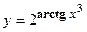
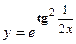


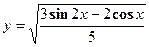
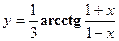
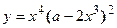
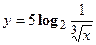
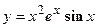
3. Найти 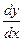
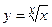
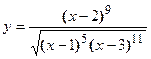
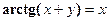
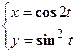
4. Показать, что функция 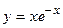 удовлетворяет уравнению
удовлетворяет уравнению 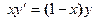
5. Найти 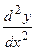
а) 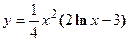 в)
в) 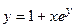
б) 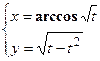
6. Найдите координаты точки пересечения двух касательных, проведенных к графику функции 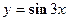 : первая в точке с абсциссой
: первая в точке с абсциссой 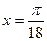 , вторая с абсциссой
, вторая с абсциссой 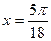
7. Будет ли выполняться теорема Ролля для функции 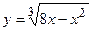 на отрезке [0, 8]. Если да, то найти соответствующее значение x.
на отрезке [0, 8]. Если да, то найти соответствующее значение x.
Вариант 2
- Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
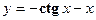
- Найти производную сложной функции
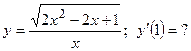
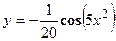
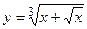
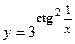
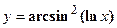
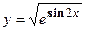
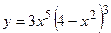
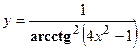
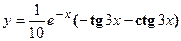
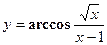

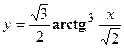
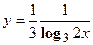
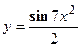
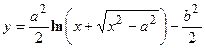
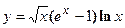
- Найти
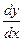
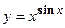
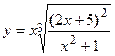
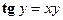
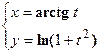
- Показать, что функция
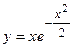 удовлетворяет уравнению
удовлетворяет уравнению 
- Найти
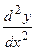
а) 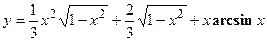 в)
в) 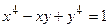
б) 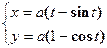
- К параболе
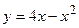 в точке на ней с абсциссой
в точке на ней с абсциссой 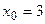 проведена касательная. Найдите точку пересечения этой касательной с осью X.
проведена касательная. Найдите точку пересечения этой касательной с осью X.
7. Записав формулу Лагранжа для функции 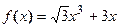 на отрезке [0, 1], найти на интервале (0, 1) соответствующее значение x.
на отрезке [0, 1], найти на интервале (0, 1) соответствующее значение x.
Вариант 3
- Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
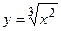
- Найти производную сложной функции
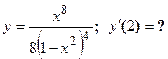
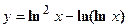
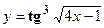
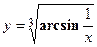
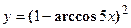
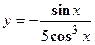
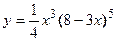
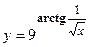
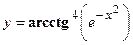
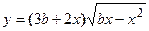
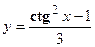
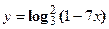
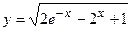
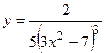
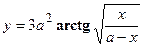
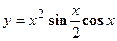
- Найти
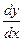
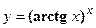
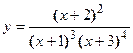
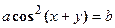
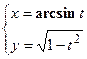
4. Показать, что функция 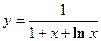 удовлетворяет уравнению
удовлетворяет уравнению 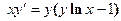
5. Найти 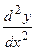
а) 
б) 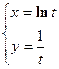 в)
в) 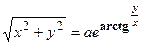
- Найдите координаты точки пересечения двух касательных, проведенных к графику функции
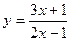 : первая в точке на графике с абсциссой
: первая в точке на графике с абсциссой 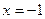 , а вторая в точке с абсциссой
, а вторая в точке с абсциссой 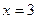 .
. - Записав формулу Коши для функций
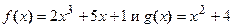 и на отрезке [0, 2], найти соответствующее значение x.
и на отрезке [0, 2], найти соответствующее значение x.
Вариант 4
- Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции

- Найти производную сложной функции
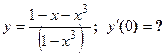
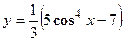

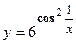
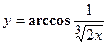
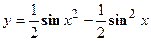
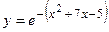
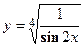
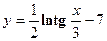
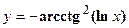
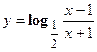
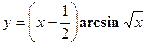
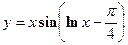

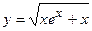
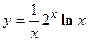
- Найти
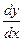
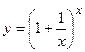
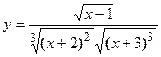
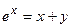
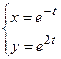
4. Показать, что функция 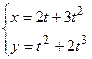 удовлетворяет уравнению
удовлетворяет уравнению 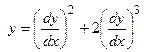

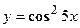
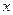 произвольное приращение
произвольное приращение 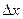 и, подставляя в данное выражение функции вместо
и, подставляя в данное выражение функции вместо 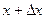 , находим наращенное значение функции
, находим наращенное значение функции 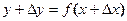
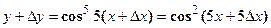
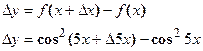
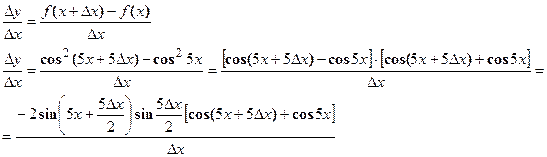
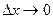 . Этот предел и даст искомую производную
. Этот предел и даст искомую производную 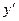 от функции
от функции 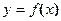 ;
; 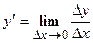
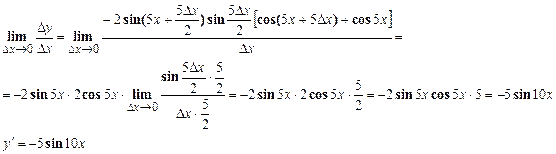
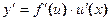
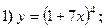
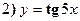
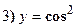
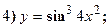
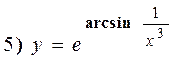
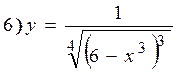
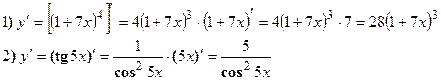
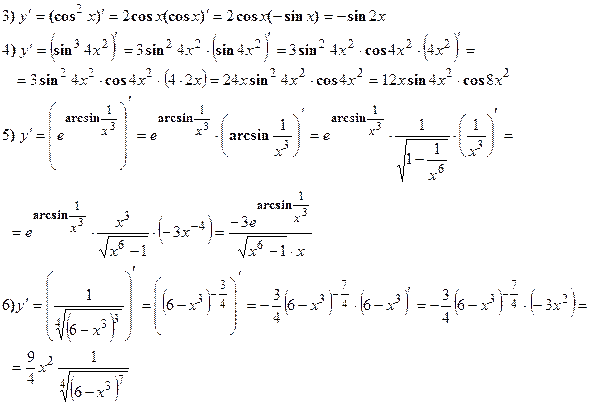
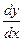 для данной неявной функции
для данной неявной функции 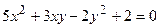
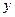 есть функция от
есть функция от 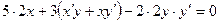 .
.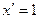 , получаем
, получаем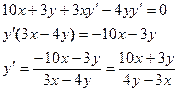
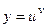 , где
, где 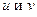 - функции от
- функции от 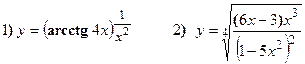
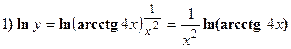
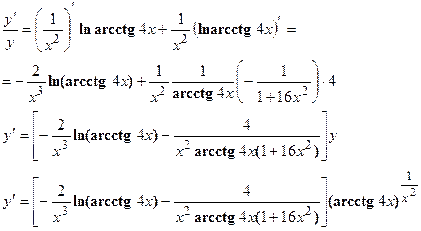
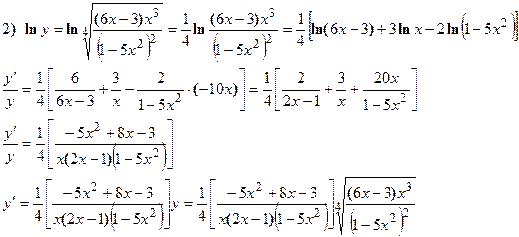
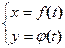
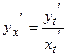
 для функции, заданной параметрически
для функции, заданной параметрически 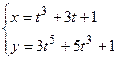
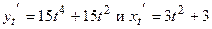 . Следовательно,
. Следовательно, 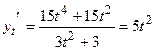
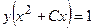 обращает уравнение
обращает уравнение 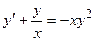 в тождество.
в тождество. . Найдем
. Найдем 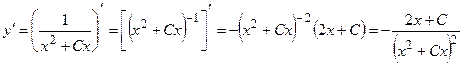
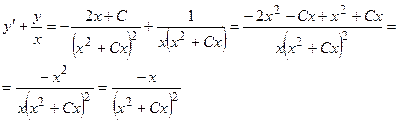

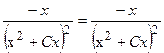 , что и требовалось доказать.
, что и требовалось доказать.
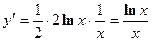 .
.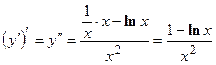
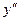 .
.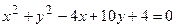
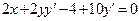
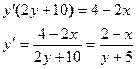
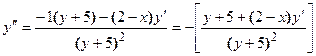
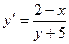 , получаем:
, получаем: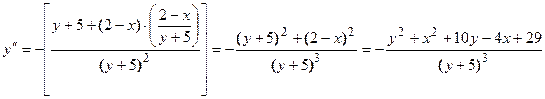 .
.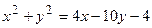 , получим
, получим 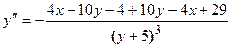 или
или 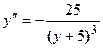
 .
.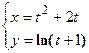
 по параметру
по параметру  .
.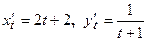
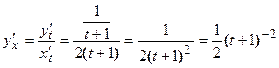
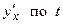 , а затем искомую вторую производную от
, а затем искомую вторую производную от 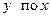 как отношение производных от
как отношение производных от 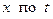 .
.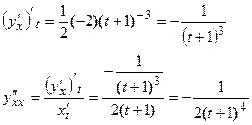
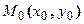 имеют вид:
имеют вид: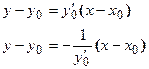 , где
, где 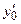 - значение в точке
- значение в точке 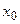 производной
производной 
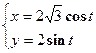 в точке, где
в точке, где 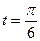 .
.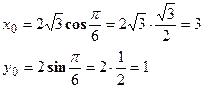 , получаем точку
, получаем точку 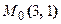
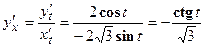
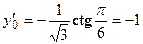 .
.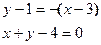
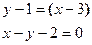
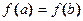 , то в интервале (a, b) существует по крайней мере одна точка с, в которой производная функции обращается в нуль:
, то в интервале (a, b) существует по крайней мере одна точка с, в которой производная функции обращается в нуль: 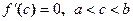 .
. на концах отрезка [0, 4] принимает равные значения
на концах отрезка [0, 4] принимает равные значения 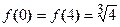 .
.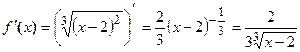 . При
. При 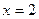 ,
, 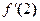 не существует. Нарушено второе условие теоремы Ролля.
не существует. Нарушено второе условие теоремы Ролля.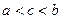 , для которой
, для которой 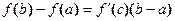 .
. и найти соответствующее промежуточное значение с.
и найти соответствующее промежуточное значение с.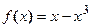 непрерывна и дифференцируема для всех значений
непрерывна и дифференцируема для всех значений 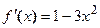 . Отсюда по формулам Лагранжа имеем
. Отсюда по формулам Лагранжа имеем
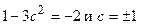 ; годится только значение
; годится только значение 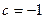 , для которого справедливо неравенство
, для которого справедливо неравенство 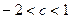 .
.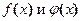 удовлетворяют следующим условиям:
удовлетворяют следующим условиям: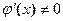 для любого
для любого 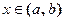 , то внутри отрезка [ a, b ] найдется такая точка
, то внутри отрезка [ a, b ] найдется такая точка 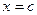 ,
, 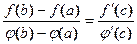
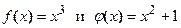 на отрезке [1; 2].
на отрезке [1; 2].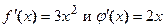 . На отрезке [1, 2],
. На отрезке [1, 2], 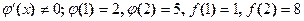 .
.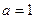 и
и 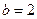 существует значение
существует значение 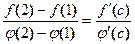
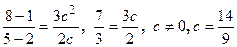 .
.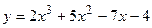
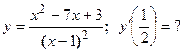
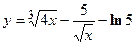
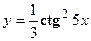
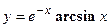
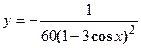
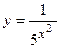
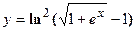
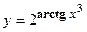
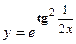


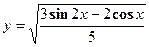
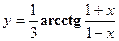
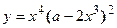
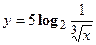
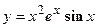
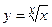
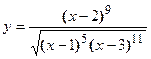
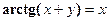
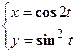
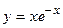 удовлетворяет уравнению
удовлетворяет уравнению 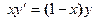
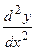
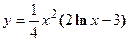 в)
в) 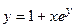
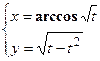
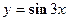 : первая в точке с абсциссой
: первая в точке с абсциссой 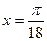 , вторая с абсциссой
, вторая с абсциссой 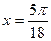
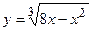 на отрезке [0, 8]. Если да, то найти соответствующее значение x.
на отрезке [0, 8]. Если да, то найти соответствующее значение x.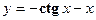
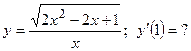
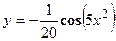
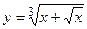
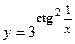
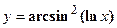
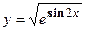
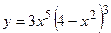
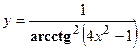
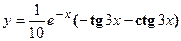
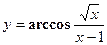

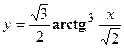
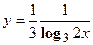
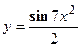
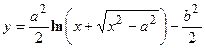
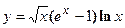
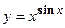
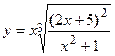
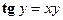
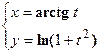
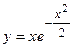 удовлетворяет уравнению
удовлетворяет уравнению 
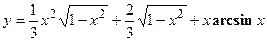 в)
в) 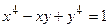
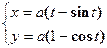
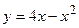 в точке на ней с абсциссой
в точке на ней с абсциссой 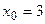 проведена касательная. Найдите точку пересечения этой касательной с осью X.
проведена касательная. Найдите точку пересечения этой касательной с осью X.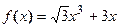 на отрезке [0, 1], найти на интервале (0, 1) соответствующее значение x.
на отрезке [0, 1], найти на интервале (0, 1) соответствующее значение x.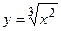
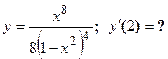
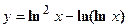
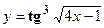
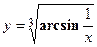
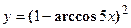
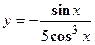
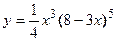
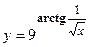
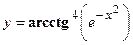
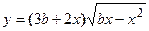
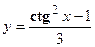
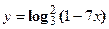
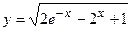
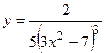
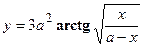
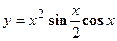
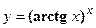
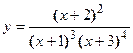
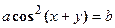
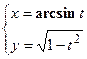
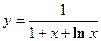 удовлетворяет уравнению
удовлетворяет уравнению 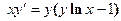

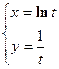 в)
в) 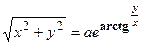
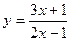 : первая в точке на графике с абсциссой
: первая в точке на графике с абсциссой 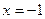 , а вторая в точке с абсциссой
, а вторая в точке с абсциссой 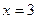 .
.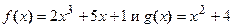 и на отрезке [0, 2], найти соответствующее значение x.
и на отрезке [0, 2], найти соответствующее значение x.
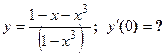
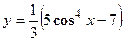

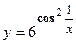
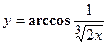
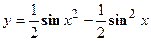
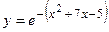
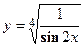
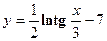
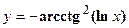
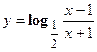
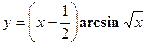
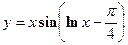

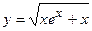
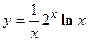
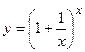
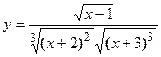
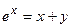
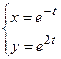
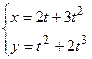 удовлетворяет уравнению
удовлетворяет уравнению