Линейные операторы.
Определение 1. Функция (отображение) А, определенная на линейном пространстве Ln, область значений которой принадлежит линейному пространству Lm (здесь n и m – размерности соответствующих пространств) называется оператором:
Если
Все прообразы нулевого элемента Lm называют ядром оператора А:
Определение 2. Оператор А называется линейным, если для
Примеры. 1) 3)
5)
Пусть А – линейный оператор:
Определение 3. Матрицей линейного оператора А называется матрица (будем обозначать ее через Аmn), столбцами которой являются координаты образов базисных элементов {e} в базисе {f }, т.е., если
Замечание. Оператор, в частности линейный, определяет некоторое действие на элементы линейного пространства и не зависит от базиса. В свою очередь, матрица линейного оператора зависит как от базиса пространства прообразов, так и от базиса пространства образов.
Преобразование j линейного пространства Vп называется линейным преобразованием этого пространства, если сумму любых двух векторов а, b оно переводит в сумму образов этих векторов,
(a+b) j =aj + bj (1)
а произведение любого вектора а на любое число а переводит в произведение образа вектора а на это же число а,
(aa) j=a(aj) (2)
Из этого определения немедленно вытекает, что линейное преобразование линейного пространства переводит любую линейную комбинацию данных векторов а1, а2,…, аn, в линейную комбинацию (с теми же коэффициентами) образов этих векторов
(a1а1+ a2 а1+… an а1)j = a1(а1j) +a2(а2j) + …+an(аnj) (3) 28. Собственные векторы линейного преобразования, векторы, которые при этом преобразовании не меняют своего направления, а только умножаются на скаляр. Например, Собственные векторы преобразования, составленного из вращении вокруг некоторой оси и сжатия к перпендикулярной ей плоскости, служат векторы, направленные по этой оси. Координаты х1, х2,..., xn Собственные векторы линейного преобразования n-мерного пространства с матрицей преобразования ||aik|| удовлетворяют системе однородных линейных уравнений
Собственные векторы и собственные значения линейного оператора
Ненулевой вектор
Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор
Собственные числа
Для каждого собственного значения
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид
где 29. Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Пусть
Функция где Свойства
|


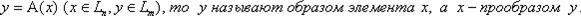
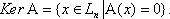
 выполняется равенство:
выполняется равенство:
 (Ø). 2)
(Ø). 2) 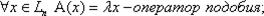
 4)
4) 

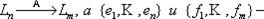 базисы в соответствующих пространствах Ln и Lm.
базисы в соответствующих пространствах Ln и Lm.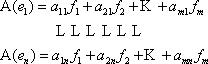 , то
, то  или в матричной форме:
или в матричной форме:
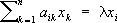 ,
,  где l — одно из собственных значений этой матрицы. Если матрица преобразования самосопряжённая (см. Самосопряжённая матрица), то Собственные векторы взаимно перпендикулярны. При самосопряжённом преобразовании сфера переходит в эллипсоид, главными осями которого являются Собственные векторы преобразования.
где l — одно из собственных значений этой матрицы. Если матрица преобразования самосопряжённая (см. Самосопряжённая матрица), то Собственные векторы взаимно перпендикулярны. При самосопряжённом преобразовании сфера переходит в эллипсоид, главными осями которого являются Собственные векторы преобразования.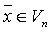 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора 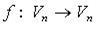 , если
, если  (
( для комплексного
для комплексного  ), такое, что
), такое, что  Число
Число  называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.
называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.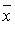 имеет координатный столбец X, то
имеет координатный столбец X, то 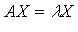 или
или 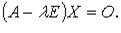
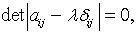 , где
, где  - матрица оператора f,
- матрица оператора f,  - символ Кронекера.
- символ Кронекера.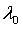 соответствующие собственные векторы могут быть найдены из матричного уравнения
соответствующие собственные векторы могут быть найдены из матричного уравнения  или соответствующей ему системы линейных уравнений
или соответствующей ему системы линейных уравнений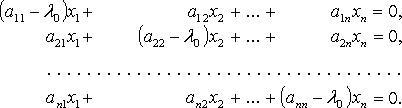

 - соответствующие собственные значения.
- соответствующие собственные значения.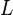 есть векторное пространство над полем
есть векторное пространство над полем  и
и 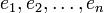 — базис в
— базис в  называется квадратичной формой, если её можно представить в виде
называется квадратичной формой, если её можно представить в виде 
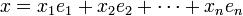 , а
, а 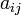 — некоторые элементы поля К.
— некоторые элементы поля К.


