Экстремум — максимальное или минимальное значение функции на заданном множестве.
Определение 1. Точку х =х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х =х0) выполняется неравенство:
f(х)>f(х0).
Определение 2. Точку х = х0 называют точкой максимума функции у=f(х), если у этой точки существует окрестность, для всех точек которой, кроме самой точки х = х0, выполняется неравенство:
f(х)<f(х0).
1. Если функция у = f(х) имеет экстремум в точке х = х0, то в этой точке производная функции либо равна нулю, либо не существует.
2. Пусть функция у=f(х) непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку x = x0. Тогда:
а) если у этой точки существует такая окрестность, что в ней при х<х0 выполняется неравенство f(x) < 0,а при x > x0 — неравенство f"x)>0, то x =x0 — точка минимума функции У=f(х);
б) если у этой точки существует такая окрестность, что в ней при x < x0 выполняется неравенство f"(x) > О, а при x > x0 —
неравенство f(х) < О, то x = x0 — точка максимума функции У=f(х);
в) если у этой точки существует такая окрестность, что в ней и слева, и справа от точки x0 знаки производной одинаковы, то в точке x = x0 экстремума нет.
АЛГОРИТМ ИССЛЕДОВАНИЯ НЕПРЕРЫВНОЙ ФУНКЦИИ у = f(х) НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ
1. Найти производную f'(х).
2. Найти стационарные и критические точки.
3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4. Сделать выводы о монотонности функции и о ее точках экстремума.
Пример 6. Исследовать функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
Решение. Заметим, что функция всюду непрерывна, кроме точки х = 0. Воспользуемся указанным выше алгоритмом.
1) Найдем производную заданной функции:

2) Производная обращается в нуль в точках х = 2 и х = -2 — это стационарные точки. Производная не существует в точке х = 0, но это не критическая точка, это точка разрыва функции (полюс).
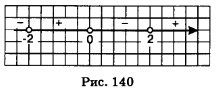
3) Отметим точки -2, 0 и 2 на числовой прямой и расставим знаки производной на получившихся промежутках (рис. 140).
4) Делаем выводы: на луче(-°°, -2] функция убывает, на полуинтервале [-2, 0) функция возрастает, на полуинтервале (0, 2] функция убывает, на луче [2, + функция возрастает.
Далее, х = -2 — точка минимума, причем 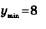 (подставили значение x= -2 в формулу
(подставили значение x= -2 в формулу 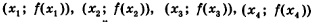
Аналогично устанавливаем, что и х = 2 точка минимума, причем 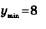
3. Построение графиков функций
За годы изучения курса алгебры в школе вы накопили достаточно большой опыт построения графиков функций. В основном вы строили графики «по точкам», т.е. для заданной функции у = f(х) находили контрольные точки 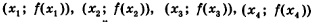 и т.д., отмечали их на координатной плоскости и, полагаясь на интуицию, соединяли найденные точки плавной кривой. Как выбирали эти контрольные точки? Иногда обдуманно, например, строили вершину параболы у=ах2 +Ъх+с или специально искали точки пересечения графика с осями координат. Но чаще выбор контрольных точек был случайным, «по наитию».
и т.д., отмечали их на координатной плоскости и, полагаясь на интуицию, соединяли найденные точки плавной кривой. Как выбирали эти контрольные точки? Иногда обдуманно, например, строили вершину параболы у=ах2 +Ъх+с или специально искали точки пересечения графика с осями координат. Но чаще выбор контрольных точек был случайным, «по наитию».
Графики любых функций строят по точкам. Но в тех случаях, когда вид графика заранее неизвестен, эти точки надо выбирать со смыслом — уметь выделять особо важные точки графика, которые определяют его структуру. Об этом мы уже говорили выше, когда строили графики функций у=2х3 +3х2 -1 и у=Зх4 -16х3 +24х2 -11. К особо важным точкам графика функции у = f(х) относят:
— стационарные и критические точки;
— точки экстремума;
— точки пересечения графика с осями координат;
— точки разрыва функции.
В тех случаях, когда речь идет о построении графика незнакомой функции, когда заранее невозможно представить вид графика, полезно применять определенную схему исследования свойств функции, которая помогает составить представление о ее графике. Когда такое представление составится, можно приступить к построению графика по точкам.
В курсе математического анализа разработана универсальная схема исследования свойств функции и построения графика функции, позволяющая строить весьма сложные графики. Для наших нужд будут достаточны упрощенные варианты указанной схемы.
1) Если функция у = f(х) непрерывна на всей числовой прямой, то достаточно найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек. Именно так мы действовали в этом параграфе, когда строили графики следующих функций:

2) Если функция у - f(х) определена не на всей числовой прямой, то начинать следует с отыскания области определения функции (если, конечно, она не задана) и с указания ее точек разрыва.
3) Полезно исследовать функцию на четность, поскольку графики четной или нечетной функции обладают симметрией (соответственно относительно оси у или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при х>0, а затем достроить симметричную ветвь.
Например, для функции ее график (гипербола) изображен на рис. 141 — вертикальной асимптотой является прямая х = 1. Если х -»1, то знаменатель данной дроби становится (по модулю)
все меньше и меньше, точнее: (х-1) —>0; соответственно сама дробь становится (по модулю) все больше и больше, точнее:
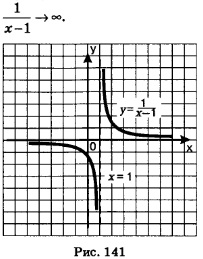
Самый распространенный признак существования вертикальной асимптоты заключается в следующем:
если  и при х = а знаменатель обращается в нуль, а числитель отличен от нуля, то х = а —вертикальная асимптота графика функции у = f(x).
и при х = а знаменатель обращается в нуль, а числитель отличен от нуля, то х = а —вертикальная асимптота графика функции у = f(x).
Задания для самостоятельного решения на понимание пройденной темы:
1. Исследуйте функцию на монотонность и экстремумы:
1) 
2) 
3) 
2. Найдите наименьшее и наибольшее значения заданной функции на заданном промежутке:
1) 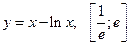
3. Найдите, если возможно, наименьшее и (или) наибольшее значения заданной функции на указанном промежутке:
1) 
2) 
4. При каких значениях параметра 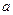 функция возрастает на всей числовой прямой?
функция возрастает на всей числовой прямой?
1) 
2) 

 на монотонность и экстремумы.
на монотонность и экстремумы.

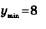 (подставили значение x= -2 в формулу
(подставили значение x= -2 в формулу 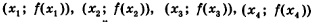


 и при х = а знаменатель обращается в нуль, а числитель отличен от нуля, то х = а —вертикальная асимптота графика функции у = f(x).
и при х = а знаменатель обращается в нуль, а числитель отличен от нуля, то х = а —вертикальная асимптота графика функции у = f(x).


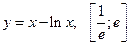


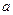 функция возрастает на всей числовой прямой?
функция возрастает на всей числовой прямой?




